In topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

 and related areas of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 a topological property or topological invariant is a property of a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 which is invariant

Invariant (mathematics)

In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...

 under homeomorphism

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

s. That is, a property of spaces is a topological property if whenever a space X possesses that property every space homeomorphic to X possesses that property. Informally, a topological property is a property of the space that can be expressed using open sets.

A common problem in topology is to decide whether two topological spaces are homeomorphic or not. To prove that two spaces are not homeomorphic, it is sufficient to find a topological property which is not shared by them.

Cardinal function

Cardinal function

In mathematics, a cardinal function is a function that returns cardinal numbers.- Cardinal functions in set theory :...

s

• The cardinality |X| of the space X.
• The cardinality τ(X) of the topology of the space X.
• Weight w(X), the least cardinality of a basis of the topology of the space X.
• Density d(X), the least cardinality of a subset of X whose closure is X.

Separation

For a detailed treatment, see separation axiom

Separation axiom

In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...

. Some of these terms are defined differently in older mathematical literature; see history of the separation axioms

History of the separation axioms

In general topology, the separation axioms have had a convoluted history, with many competing meanings for the same term, and many competing terms for the same concept.- Origins :...

.

• T₀ or Kolmogorov. A space is Kolmogorov
  Kolmogorov space
  In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
  
   if for every pair of distinct points x and y in the space, there is at least either an open set containing x but not y, or an open set containing y but not x.
• T₁ or Fréchet. A space is Fréchet
  T1 space
  In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
  
   if for every pair of distinct points x and y in the space, there is an open set containing x but not y. (Compare with T₀; here, we are allowed to specify which point will be contained in the open set.) Equivalently, a space is T₁ if all its singletons are closed. T₁ spaces are always T₀.
• Sober. A space is sober
  Sober space
  In mathematics, a sober space is a topological spacesuch that every irreducible closed subset of X is the closure of exactly one point of X: that is, has a unique generic point.-Properties and examples :...
  
   if every irreducible closed set C has a unique generic point p. In other words, if C is not the (possibly nondisjoint) union of two smaller closed subsets, then there is a p such that the closure of {p} equals C, and p is the only point with this property.
• T₂ or Hausdorff. A space is Hausdorff
  Hausdorff space
  In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
  
   if every two distinct points have disjoint neighbourhoods. T₂ spaces are always T₁.
• T_2½ or Urysohn. A space is Urysohn  if every two distinct points have disjoint closed neighbourhoods. T_2½ spaces are always T₂.
• Regular. A space is regular
  Regular space
  In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
  
   if whenever C is a closed set and p is a point not in C, then C and p have disjoint neighbourhoods.
• T₃ or Regular Hausdorff. A space is regular Hausdorff if it is a regular T₀ space. (A regular space is Hausdorff if and only if it is T₀, so the terminology is consistent.)
• Completely regular. A space is completely regular
  Tychonoff space
  In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
  
   if whenever C is a closed set and p is a point not in C, then C and {p} are separated by a function.
• T_3½, Tychonoff, Completely regular Hausdorff or Completely T₃. A Tychonoff space
  Tychonoff space
  In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
  
   is a completely regular T₀ space. (A completely regular space is Hausdorff if and only if it is T₀, so the terminology is consistent.) Tychonoff spaces are always regular Hausdorff.
• Normal. A space is normal
  Normal space
  In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
  
   if any two disjoint closed sets have disjoint neighbourhoods. Normal spaces admit partitions of unity.
• T₄ or Normal Hausdorff. A normal space is Hausdorff if and only if it is T₁. Normal Hausdorff spaces are always Tychonoff.
• Completely normal. A space is completely normal if any two separated sets have disjoint neighbourhoods.
• T₅ or Completely normal Hausdorff. A completely normal space is Hausdorff if and only if it is T₁. Completely normal Hausdorff spaces are always normal Hausdorff.
• Perfectly normal. A space is perfectly normal if any two disjoint closed sets are precisely separated by a function. A perfectly normal space must also be completely normal.
• Perfectly normal Hausdorff, or perfectly T₄. A space is perfectly normal Hausdorff, if it is both perfectly normal and T₁. A perfectly normal Hausdorff space must also be completely normal Hausdorff.
• Discrete space. A space is discrete
  Discrete space
  In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
  
   if all of its points are completely isolated, i.e. if any subset is open.

Countability conditions

• Separable. A space is separable if it has a countable dense subset.
• Lindelöf. A space is Lindelöf
  Lindelöf space
  In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
  
   if every open cover has a countable subcover.
• First-countable. A space is first-countable
  First-countable space
  In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
  
   if every point has a countable local base.
• Second-countable. A space is second-countable
  Second-countable space
  In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
  
   if it has a countable base for its topology. Second-countable spaces are always separable, first-countable and Lindelöf.

Connectedness

• Connected. A space is connected
  Connected space
  In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
  
   if it is not the union of a pair of disjoint non-empty open sets. Equivalently, a space is connected if the only clopen set
  Clopen set
  In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
  
  s are the empty set and itself.
• Locally connected. A space is locally connected if every point has a local base consisting of connected sets.
• Totally disconnected. A space is totally disconnected if it has no connected subset with more than one point.
• Path-connected. A space X is path-connected if for every two points x, y in X, there is a path p from x to y, i.e., a continuous map p: [0,1] → X with p(0) = x and p(1) = y. Path-connected spaces are always connected.
• Locally path-connected. A space is locally path-connected if every point has a local base consisting of path-connected sets. A locally path-connected space is connected if and only if it is path-connected.
• Simply connected. A space X is simply connected if it is path-connected and every continuous map f: S¹ → X is homotopic to a constant map.
• Locally simply connected. A space X is locally simply connected
  Locally simply connected space
  In mathematics, a locally simply connected space is a topological space that admits a basis of simply connected sets. Every locally simply connected space is also locally path-connected and locally connected....
  
   if every point x in X has a local base of neighborhoods U that is simply connected.
• Semi-locally simply connected. A space X is semi-locally simply connected
  Semi-locally simply connected
  In mathematics, specifically algebraic topology, the phrase semi-locally simply connected refers to a certain local connectedness condition that arises in the theory of covering spaces. Roughly speaking, a topological space X is semi-locally simply connected if there is a lower bound on the sizes...
  
   if every point has a local base of neighborhoods U such that every loop in U is contractible in X. Semi-local simple connectivity, a strictly weaker condition than local simple connectivity, is a necessary condition for the existence of a universal cover.
• Contractible. A space X is contractible if the identity map
  Identity function
  In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
  
   on X is homotopic to a constant map. Contractible spaces are always simply connected.
• Hyper-connected. A space is hyper-connected if no two non-empty open sets are disjoint. Every hyper-connected space is connected.
• Ultra-connected. A space is ultra-connected if no two non-empty closed sets are disjoint. Every ultra-connected space is path-connected.
• Indiscrete or trivial. A space is indiscrete if the only open sets are the empty set and itself. Such a space is said to have the trivial topology
  Trivial topology
  In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
  
  .

Compactness

• Compact. A space is compact
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
   if every open cover has a finite subcover. Some authors call these spaces quasicompact and reserve compact for Hausdorff
  Hausdorff space
  In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
  
   spaces where every open cover has finite subcover. Compact spaces are always Lindelöf and paracompact. Compact Hausdorff spaces are therefore normal.
• Sequentially compact. A space is sequentially compact if every sequence has a convergent subsequence.
• Countably compact. A space is countably compact if every countable open cover has a finite subcover.
• Pseudocompact. A space is pseudocompact if every continuous real-valued function on the space is bounded.
• σ-compact. A space is σ-compact if it is the union of countably many compact subsets.
• Paracompact. A space is paracompact if every open cover has an open locally finite refinement. Paracompact Hausdorff spaces are normal.
• Locally compact. A space is locally compact if every point has a local base consisting of compact neighbourhoods. Slightly different definitions are also used. Locally compact Hausdorff spaces are always Tychonoff.
• Ultraconnected compact. In an ultra-connected compact space X every open cover must contain X itself. Non-empty ultra-connected compact spaces have a largest proper open subset called a monolith.

Metrizability

• Metrizable. A space is metrizable if it is homeomorphic to a metric space
  Metric space
  In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
  
  . Metrizable spaces are always Hausdorff and paracompact (and hence normal and Tychonoff), and first-countable.
• Polish. A space is called Polish if it is metrizable with a separable and complete metric.
• Locally metrizable. A space is locally metrizable if every point has a metrizable neighbourhood.

Miscellaneous

• Baire space. A space X is a Baire space
  Baire space
  In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
  
   if it is not meagre in itself. Equivalently, X is a Baire space if the intersection of countably many dense open sets is dense.
• Homogeneous. A space X is homogeneous if for every x and y in X there is a homeomorphism f : X → X such that f(x) = y. Intuitively speaking, this means that the space looks the same at every point. All topological group
  Topological group
  In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
  
  s are homogeneous.
• Finitely generated or Alexandrov. A space X is Alexandrov
  Alexandrov topology
  In topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
  
   if arbitrary intersections of open sets in X are open, or equivalently if arbitrary unions of closed sets are closed. These are precisely the finitely generated
  Finitely generated
  In mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
  
   members of the category of topological spaces
  Category of topological spaces
  In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
  
   and continuous maps.
• Zero-dimensional. A space is zero-dimensional if it has a base of clopen sets. These are precisely the spaces with a small inductive dimension
  Inductive dimension
  In the mathematical field of topology, the inductive dimension of a topological space X is either of two values, the small inductive dimension ind or the large inductive dimension Ind...
  
   of 0.
• Almost discrete. A space is almost discrete if every open set is closed (hence clopen). The almost discrete spaces are precisely the finitely generated zero-dimensional spaces.
• Boolean. A space is Boolean if it is zero-dimensional, compact and Hausdorff (equivalently, totally disconnected, compact and Hausdorff). These are precisely the spaces that are homeomorphic to the Stone spaces of Boolean algebras.
• Reidemeister torsion
• -resolvable. A space is said to be κ-resolvable (respectively: almost κ-resolvable) if it contains κ dense sets that are pairwise disjoint (respectively: almost disjoint over the ideal of nowhere dense subsets). If the space is not -resolvable then it is called -irresolvable.
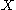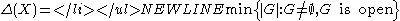• Maximally resolvable. Space is maximally resolvable if it is -resolvable, where . Number 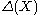is called dispersion character of .
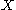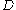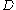  • Strongly discrete. Set is strongly discrete subset of the space if the points in may be separated by pairwise disjoint neighborhoods. Space 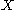is said to be strongly discrete if every non-isolated point of 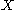is the accumulation point of some strongly discrete set.
  
  

  See also

  • Euler characteristic
    Euler characteristic
    In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
    
    
  • Winding number
    Winding number
    In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
    
    
  • Knot invariant
    Knot invariant
    In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
    
    
  • Linking number
    Linking number
    In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other...
    
    
  • Fixed point property
    Fixed point property
    A mathematical object X has the fixed-point property if every suitably well-behaved mapping from X to itself has a fixed point. It is a special case of the fixed morphism property. The term is most commonly used to describe topological spaces on which every continuous mapping has a fixed point...
    
    
  • Topological quantum number
    Topological quantum number
    In physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...
    
    
  • Homotopy group
    Homotopy group
    In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
    
     and Cohomotopy group
    Cohomotopy group
    In mathematics, particularly algebraic topology, cohomotopy sets are particular contravariant functors from the category of pointed topological spaces and point-preserving continuous maps to the category of sets and functions...
    
    
  • Homology
    Homology (mathematics)
    In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
    
     and cohomology
    Cohomology
    In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
    
    
  • Quantum invariant
    Quantum invariant
    In the mathematical field of knot theory, a quantum invariant of a knot or link is a linear sum of colored Jones polynomial of surgery presentations of the knot complement.-List of invariants:*Finite type invariant*Kontsevich invariant*Kashaev's invariant...
    
    
  The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.