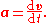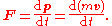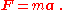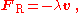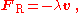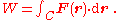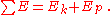
Classical mechanics
Encyclopedia
In physics
, classical mechanics is one of the two major sub-fields of mechanics
, which is concerned with the set of physical law
s describing the motion of bodies
under the action of a system of forces. The study of the motion of bodies is an ancient one, making classical mechanics one of the oldest and largest subjects in science
, engineering
and technology
.
Classical mechanics describes the motion of macroscopic
objects, from projectiles to parts of machinery, as well as astronomical objects, such as spacecraft
, planets, star
s, and galaxies. Besides this, many specializations within the subject deal with gas
es, liquid
s, solid
s, and other specific sub-topics. Classical mechanics provides extremely accurate results as long as the domain of study is restricted to large objects and the speeds involved do not approach the speed of light
. When the objects being dealt with become sufficiently small, it becomes necessary to introduce the other major sub-field of mechanics, quantum mechanics
, which reconciles the macroscopic laws of physics with the atomic nature of matter
and handles the wave-particle duality of atom
s and molecule
s. In the case of high velocity
objects approaching the speed of light, classical mechanics is enhanced by special relativity
. General relativity
unifies special relativity with Newton's law of universal gravitation
, allowing physicists to handle gravitation
at a deeper level.
The term classical mechanics was coined in the early 20th century to describe the system of physics begun by Isaac Newton
and many contemporary 17th century natural philosophers, building upon the earlier astronomical theories of Johannes Kepler
, which in turn were based on the precise observations of Tycho Brahe
and the studies of terrestrial projectile motion
of Galileo
. Because these aspects of physics were developed long before the emergence of quantum physics and relativity, some sources exclude Einstein's theory of relativity
from this category. However, a number of modern sources do include relativistic mechanics, which in their view represents classical mechanics in its most developed and most accurate form.
The notion of "classical" may be somewhat confusing, insofar as this term usually refers to the era of classical antiquity
in European history. While many discoveries within the mathematics
of that period remain in full force today, and of the greatest use, much of the science that emerged then has since been superseded by more accurate models. This in no way detracts from the science of that time, though as most of modern physics is built directly upon the important developments, especially within technology, which took place in antiquity and during the Middle Ages
in Europe and elsewhere. However, the emergence of classical mechanics was a decisive stage in the development of science
, in the modern sense of the term. What characterizes it, above all, is its insistence on mathematics
(rather than speculation
), and its reliance on experiment
(rather than observation
). With classical mechanics it was established how to formulate quantitative predictions in theory
, and how to test them by carefully designed measurement
. The emerging globally cooperative endeavor increasingly provided for much closer scrutiny and testing, both of theory and experiment. This was, and remains, a key factor in establishing certain knowledge, and in bringing it to the service of society. History shows how closely the health and wealth of a society depends on nurturing this investigative and critical approach.
The initial stage in the development of classical mechanics is often referred to as Newtonian mechanics, and is associated with the physical concepts employed by and the mathematical methods invented by Newton himself, in parallel with Leibniz, and others. This is further described in the following sections. Later, more abstract and general methods were developed, leading to reformulations of classical mechanics known as Lagrangian mechanics
and Hamiltonian mechanics
. These advances were largely made in the 18th and 19th centuries, and they extend substantially beyond Newton's work, particularly through their use of analytical mechanics
. Ultimately, the mathematics developed for these were central to the creation of quantum mechanics.
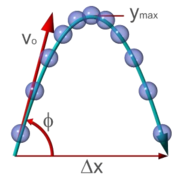The following introduces the basic concepts of classical mechanics. For simplicity, it often models real-world objects as point particle
s, objects with negligible
size. The motion of a point particle is characterized by a small number of parameter
s: its position, mass
, and the force
s applied to it. Each of these parameters is discussed in turn.
In reality, the kind of objects that classical mechanics can describe always have a non-zero size. (The physics of very small particles, such as the electron
, is more accurately described by quantum mechanics
). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom
—for example, a baseball
can spin
while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made up of a large number of interacting point particles. The center of mass
of a composite object behaves like a point particle.
The position of a point particle
is defined with respect to an arbitrary fixed reference point, O, in space
, usually accompanied by a coordinate system
, with the reference point located at the origin of the coordinate system. It is defined as the vector r from O to the particle
. In general, the point particle need not be stationary relative to O, so r is a function of t, the time
elapsed since an arbitrary initial time. In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval between any given pair of events is the same for all observers. In addition to relying on absolute time, classical mechanics assumes Euclidean geometry
for the structure of space.
, or the rate of change
of position with time, is defined as the derivative
of the position with respect to time or
In classical mechanics, velocities are directly additive and subtractive. For example, if one car traveling East at 60 km/h passes another car traveling East at 50 km/h, then from the perspective of the slower car, the faster car is traveling east at 60 − 50 = 10 km/h. Whereas, from the perspective of the faster car, the slower car is moving 10 km/h to the West. Velocities are directly additive as vector quantities; they must be dealt with using vector analysis.
Mathematically, if the velocity of the first object in the previous discussion is denoted by the vector and the velocity of the second object by the vector , where u is the speed of the first object, v is the speed of the second object, and d and e are unit vectors in the directions of motion of each particle respectively, then the velocity of the first object as seen by the second object is
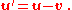
Similarly,
When both objects are moving in the same direction, this equation can be simplified to
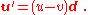
Or, by ignoring direction, the difference can be given in terms of speed only:
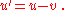
, or rate of change of velocity, is the derivative
of the velocity with respect to time (the second derivative
of the position with respect to time) or
Acceleration can arise from a change with time of the magnitude of the velocity or of the direction of the velocity or both. If only the magnitude v of the velocity decreases, this is sometimes referred to as deceleration, but generally any change in the velocity with time, including deceleration, is simply referred to as acceleration.
and acceleration of a particle
can be referred to any observer
in any state of motion, classical mechanics assumes the existence of a special family of reference frames
in terms of which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames. An inertial frame is such that when an object without any force interactions(an idealized situation) is viewed from it, it will appear either to be at rest or in a state of uniform motion in a straight line. This is the fundamental definition of an inertial frame. They are characterized by the requirement that all forces entering the observer's physical law
s originate in identifiable sources (charges, gravitational bodies, and so forth). A non-inertial reference frame is one accelerating with respect to an inertial one, and in such a non-inertial frame a particle is subject to acceleration by fictitious force
s that enter the equations of motion solely as a result of its accelerated motion, and do not originate in identifiable sources. These fictitious forces are in addition to the real forces recognized in an inertial frame. A key concept of inertial frames is the method for identifying them. For practical purposes, reference frames that are unaccelerated with respect to the distant stars
are regarded as good approximations to inertial frames.
Consider two reference frames S and S' . For observers in each of the reference frames an event has space-time coordinates of (x,y,z,t) in frame S and (x′,y′,z′,t′) in frame S′. Assuming time is measured the same in all reference frames, and if we require x = x when t = 0, then the relation between the space-time coordinates of the same event observed from the reference frames S′ and S, which are moving at a relative velocity of u in the x direction is:
This set of formulas defines a group transformation known as the Galilean transformation
(informally, the Galilean transform). This group is a limiting case of the Poincaré group
used in special relativity
. The limiting case applies when the velocity u is very small compared to c, the speed of light
.
The transformations have the following consequences:
For some problems, it is convenient to use rotating coordinates (reference frames). Thereby one can either keep a mapping to a convenient inertial frame, or introduce additionally a fictitious centrifugal force and Coriolis force.
was the first to mathematically express the relationship between force
and momentum
. Some physicists interpret Newton's second law of motion
as a definition of force and mass, while others consider it to be a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":
The quantity mv is called the (canonical) momentum
. The net force on a particle is thus equal to rate change of momentum
of the particle with time. Since the definition of acceleration is a = dv/dt, the second law can be written in the simplified and more familiar form:
So long as the force acting on a particle is known, Newton's second law is sufficient to describe the motion of a particle. Once independent relations for each force acting on a particle are available, they can be substituted into Newton's second law to obtain an ordinary differential equation
, which is called the equation of motion.
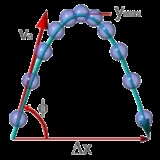
As an example, assume that friction is the only force acting on the particle, and that it may be modeled as a function of the velocity of the particle, for example:
where λ is a positive constant. Then the equation of motion is
This can be integrated
to obtain
where v0 is the initial velocity. This means that the velocity of this particle decays exponentially to zero as time progresses. In this case, an equivalent viewpoint is that the kinetic energy of the particle is absorbed by friction (which converts it to heat energy in accordance with the conservation of energy
), slowing it down. This expression can be further integrated to obtain the position r of the particle as a function of time.
Important forces include the gravitational force and the Lorentz force
for electromagnetism
. In addition, Newton's third law can sometimes be used to deduce the forces acting on a particle: if it is known that particle A exerts a force F on another particle B, it follows that B must exert an equal and opposite reaction force, −F, on A. The strong form of Newton's third law requires that F and −F act along the line connecting A and B, while the weak form does not. Illustrations of the weak form of Newton's third law are often found for magnetic forces.
More generally, if the force varies as a function of position as the particle moves from r1 to r2 along a path C, the work done on the particle is given by the line integral
If the work done in moving the particle from r1 to r2 is the same no matter what path is taken, the force is said to be conservative
. Gravity is a conservative force, as is the force due to an idealized spring
, as given by Hooke's law
. The force due to friction
is non-conservative.
The kinetic energy
Ek of a particle of mass m travelling at speed v is given by
For extended objects composed of many particles, the kinetic energy of the composite body is the sum of the kinetic energies of the particles.
The work-energy theorem states that for a particle of constant mass m the total work W done on the particle from position r1 to r2 is equal to the change in kinetic energy
Ek of the particle:
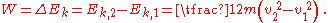
Conservative forces can be expressed as the gradient
of a scalar function, known as the potential energy
and denoted Ep:
If all the forces acting on a particle are conservative, and Ep is the total potential energy
(which is defined as a work of involved forces to rearrange mutual positions of bodies), obtained by summing the potential energies corresponding to each force
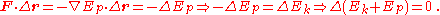
This result is known as conservation of energy and states that the total energy
,
is constant in time. It is often useful, because many commonly encountered forces are conservative.
provide extensions to Newton's laws in this area. The concepts of angular momentum
rely on the same calculus
used to describe one-dimensional motion. The rocket equation extends the notion of rate of change of an object's momentum to include the effects of an object "losing mass".
There are two important alternative formulations of classical mechanics: Lagrangian mechanics
and Hamiltonian mechanics
. These, and other modern formulations, usually bypass the concept of "force", instead referring to other physical quantities, such as energy, for describing mechanical systems.
The expressions given above for momentum and kinetic energy are only valid when there is no significant electromagnetic contribution. In electromagnetism, Newton's second law for current-carrying wires breaks down unless one includes the electromagnetic field contribution to the momentum of the system as expressed by the Poynting vector
divided by c2, where c is the speed of light
in free space.
of antiquity, among them Aristotle
, founder of Aristotelian physics
, may have been the first to maintain the idea that "everything happens for a reason" and that theoretical principles can assist in the understanding of nature. While to a modern reader, many of these preserved ideas come forth as eminently reasonable, there is a conspicuous lack of both mathematical theory
and controlled experiment
, as we know it. These both turned out to be decisive factors in forming modern science, and they started out with classical mechanics.
The medieval “science of weights” (i.e., mechanics) owes much of its importance to the work of Jordanus de Nemore. In the Elementa super demonstrationem ponderum, he introduces the concept of “positional gravity” and the use of component forces.
The first published causal explanation of the motions of planets was Johannes Kepler's Astronomia nova
published in 1609. He concluded, based on Tycho Brahe
's observations of the orbit of Mars
, that the orbits were ellipses. This break with ancient thought
was happening around the same time that Galilei
was proposing abstract mathematical laws for the motion of objects. He may (or may not) have performed the famous experiment of dropping two cannon balls of different weights from the tower of Pisa
, showing that they both hit the ground at the same time. The reality of this experiment is disputed, but, more importantly, he did carry out quantitative experiments by rolling balls on an inclined plane
. His theory of accelerated motion derived from the results of such experiments, and forms a cornerstone of classical mechanics.
As foundation for his principles of natural philosophy, Newton
proposed three laws of motion
: the law of inertia, his second law of acceleration (mentioned above), and the law of action and reaction; and hence laid the foundations for classical mechanics. Both Newton's second and third laws were given proper scientific and mathematical treatment in Newton's Philosophiæ Naturalis Principia Mathematica, which distinguishes them from earlier attempts at explaining similar phenomena, which were either incomplete, incorrect, or given little accurate mathematical expression. Newton also enunciated the principles of conservation of momentum and angular momentum
. In Mechanics, Newton was also the first to provide the first correct scientific and mathematical formulation of gravity in Newton's law of universal gravitation
. The combination of Newton's laws of motion and gravitation provide the fullest and most accurate description of classical mechanics. He demonstrated that these laws apply to everyday objects as well as to celestial objects. In particular, he obtained a theoretical explanation of Kepler's laws of motion of the planets.
Newton previously invented the calculus
, of mathematics, and used it to perform the mathematical calculations. For acceptability, his book, the Principia
, was formulated entirely in terms of the long established geometric methods, which were soon to be eclipsed by his calculus. However it was Leibniz who developed the notation of the derivative
and integral
preferred today.
Newton, and most of his contemporaries, with the notable exception of Huygens, worked on the assumption that classical mechanics would be able to explain all phenomena, including light
, in the form of geometric optics. Even when discovering the so-called Newton's rings
(a wave interference phenomenon) his explanation remained with his own corpuscular theory of light.
After Newton, classical mechanics became a principal field of study in mathematics as well as physics. After Newton there were several re-formulations which progressively allowed a solution to be found to a far greater number of problems. The first notable re-formulation was in 1788 by Joseph Louis Lagrange
. Lagrangian mechanics was in turn re-formulated in 1833 by William Rowan Hamilton
.
Some difficulties were discovered in the late 19th century that could only be resolved by more modern physics. Some of these difficulties related to compatibility with electromagnetic theory, and the famous Michelson-Morley experiment
. The resolution of these problems led to the special theory of relativity, often included in the term classical mechanics.
A second set of difficulties were related to thermodynamics. When combined with thermodynamics
, classical mechanics leads to the Gibbs paradox
of classical statistical mechanics
, in which entropy
is not a well-defined quantity. Black-body radiation was not explained without the introduction of quanta
. As experiments reached the atomic level, classical mechanics failed to explain, even approximately, such basic things as the energy levels and sizes of atoms and the photo-electric effect. The effort at resolving these problems led to the development of quantum mechanics
.
Since the end of the 20th century, the place of classical mechanics in physics
has been no longer that of an independent theory. Emphasis has shifted to understanding the fundamental forces of nature as in the Standard model
and its more modern extensions into a unified theory of everything
. Classical mechanics is a theory for the study of the motion of non-quantum mechanical, low-energy particles in weak gravitational fields.
In the 21st century classical mechanics has been extended into the complex domain and complex classical mechanics exhibits behaviours very similar to quantum mechanics.
and relativistic statistical mechanics
. Geometric optics is an approximation to the quantum theory of light
, and does not have a superior "classical" form.
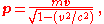
where m is the particle's mass, v its velocity, and c is the speed of light.
If v is very small compared to c, v2/c2 is approximately zero, and so
Thus the Newtonian equation is an approximation of the relativistic equation for bodies moving with low speeds compared to the speed of light.
For example, the relativistic cyclotron frequency of a cyclotron
, gyrotron
, or high voltage magnetron is given by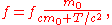
where fc is the classical frequency of an electron (or other charged particle) with kinetic energy T and (rest
) mass m0 circling in a magnetic field.
The (rest) mass of an electron is 511 keV.
So the frequency correction is 1% for a magnetic vacuum tube with a 5.11 kV direct current accelerating voltage.
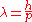
where h is Planck's constant and p is the momentum.
Again, this happens with electrons before it happens with heavier particles. For example, the electrons used by Clinton Davisson
and Lester Germer
in 1927, accelerated by 54 volts, had a wave length of 0.167 nm, which was long enough to exhibit a single diffraction
side lobe
when reflecting from the face of a nickel crystal
with atomic spacing of 0.215 nm.
With a larger vacuum chamber
, it would seem relatively easy to increase the angular resolution
from around a radian to a milliradian and see quantum diffraction from the periodic patterns of integrated circuit
computer memory.
More practical examples of the failure of classical mechanics on an engineering scale are conduction by quantum tunneling in tunnel diode
s and very narrow transistor
gates in integrated circuit
s.
Classical mechanics is the same extreme high frequency approximation
as geometric optics. It is more often accurate because it describes particles and bodies with rest mass. These have more momentum and therefore shorter De Broglie wavelengths than massless particles, such as light, with the same kinetic energies.
Classical mechanics was traditionally divided into three main branches:
Another division is based on the choice of mathematical formalism:
Alternatively, a division can be made by region of application:
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, classical mechanics is one of the two major sub-fields of mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, which is concerned with the set of physical law
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
s describing the motion of bodies
Physical body
In physics, a physical body or physical object is a collection of masses, taken to be one...
under the action of a system of forces. The study of the motion of bodies is an ancient one, making classical mechanics one of the oldest and largest subjects in science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and technology
Technology
Technology is the making, usage, and knowledge of tools, machines, techniques, crafts, systems or methods of organization in order to solve a problem or perform a specific function. It can also refer to the collection of such tools, machinery, and procedures. The word technology comes ;...
.
Classical mechanics describes the motion of macroscopic
Macroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
objects, from projectiles to parts of machinery, as well as astronomical objects, such as spacecraft
Spacecraft
A spacecraft or spaceship is a craft or machine designed for spaceflight. Spacecraft are used for a variety of purposes, including communications, earth observation, meteorology, navigation, planetary exploration and transportation of humans and cargo....
, planets, star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, and galaxies. Besides this, many specializations within the subject deal with gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es, liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s, solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
s, and other specific sub-topics. Classical mechanics provides extremely accurate results as long as the domain of study is restricted to large objects and the speeds involved do not approach the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. When the objects being dealt with become sufficiently small, it becomes necessary to introduce the other major sub-field of mechanics, quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, which reconciles the macroscopic laws of physics with the atomic nature of matter
Atomic model
In model theory, an atomic model is a model such that the complete type of every tuple is axiomatized by a single formula. Such types are called principal types, and the formulas that axiomatize them are called complete formulas.-Definitions:...
and handles the wave-particle duality of atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s and molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s. In the case of high velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
objects approaching the speed of light, classical mechanics is enhanced by special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. General relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
unifies special relativity with Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
, allowing physicists to handle gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
at a deeper level.
The term classical mechanics was coined in the early 20th century to describe the system of physics begun by Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and many contemporary 17th century natural philosophers, building upon the earlier astronomical theories of Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, which in turn were based on the precise observations of Tycho Brahe
Tycho Brahe
Tycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
and the studies of terrestrial projectile motion
Projectile motion
The motion in which a body is thrown or projected is called Projectile motion.The path followed by a projectile is called its trajectory, which is directly influenced by gravity....
of Galileo
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
. Because these aspects of physics were developed long before the emergence of quantum physics and relativity, some sources exclude Einstein's theory of relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
from this category. However, a number of modern sources do include relativistic mechanics, which in their view represents classical mechanics in its most developed and most accurate form.
The notion of "classical" may be somewhat confusing, insofar as this term usually refers to the era of classical antiquity
Classical antiquity
Classical antiquity is a broad term for a long period of cultural history centered on the Mediterranean Sea, comprising the interlocking civilizations of ancient Greece and ancient Rome, collectively known as the Greco-Roman world...
in European history. While many discoveries within the mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of that period remain in full force today, and of the greatest use, much of the science that emerged then has since been superseded by more accurate models. This in no way detracts from the science of that time, though as most of modern physics is built directly upon the important developments, especially within technology, which took place in antiquity and during the Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
in Europe and elsewhere. However, the emergence of classical mechanics was a decisive stage in the development of science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
, in the modern sense of the term. What characterizes it, above all, is its insistence on mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
(rather than speculation
Speculation
In finance, speculation is a financial action that does not promise safety of the initial investment along with the return on the principal sum...
), and its reliance on experiment
Experiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
(rather than observation
Observation
Observation is either an activity of a living being, such as a human, consisting of receiving knowledge of the outside world through the senses, or the recording of data using scientific instruments. The term may also refer to any data collected during this activity...
). With classical mechanics it was established how to formulate quantitative predictions in theory
Theory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
, and how to test them by carefully designed measurement
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
. The emerging globally cooperative endeavor increasingly provided for much closer scrutiny and testing, both of theory and experiment. This was, and remains, a key factor in establishing certain knowledge, and in bringing it to the service of society. History shows how closely the health and wealth of a society depends on nurturing this investigative and critical approach.
The initial stage in the development of classical mechanics is often referred to as Newtonian mechanics, and is associated with the physical concepts employed by and the mathematical methods invented by Newton himself, in parallel with Leibniz, and others. This is further described in the following sections. Later, more abstract and general methods were developed, leading to reformulations of classical mechanics known as Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
and Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
. These advances were largely made in the 18th and 19th centuries, and they extend substantially beyond Newton's work, particularly through their use of analytical mechanics
Analytical mechanics
Analytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
. Ultimately, the mathematics developed for these were central to the creation of quantum mechanics.
Description of the theory
Point particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
s, objects with negligible
Negligible
Negligible refers to the quantities so small that they can be ignored when studying the larger effect. Although related to the more mathematical concepts of infinitesimal, the idea of negligibility is particularly useful in practical disciplines like physics, chemistry, mechanical and electronic...
size. The motion of a point particle is characterized by a small number of parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s: its position, mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, and the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s applied to it. Each of these parameters is discussed in turn.
In reality, the kind of objects that classical mechanics can describe always have a non-zero size. (The physics of very small particles, such as the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
, is more accurately described by quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
—for example, a baseball
Baseball
Baseball is a bat-and-ball sport played between two teams of nine players each. The aim is to score runs by hitting a thrown ball with a bat and touching a series of four bases arranged at the corners of a ninety-foot diamond...
can spin
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made up of a large number of interacting point particles. The center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
of a composite object behaves like a point particle.
Position and its derivatives
| The SI Si Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system... derived "mechanical" (that is, not electromagnetic Electromagnetism Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation... or thermal Thermal physics Thermal physics is the combined study of thermodynamics, statistical mechanics, and kinetic theory. This umbrella-subject is typically designed for physics students and functions to provide a general introduction to each of three core heat-related subjects... ) units with kg, m and s Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |
|
| Position | m |
| Angular position/Angle Angle In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc... |
unitless (radian) |
| velocity Velocity In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ... |
m s−1 |
| Angular velocity Angular velocity In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per... |
s−1 |
| acceleration Acceleration In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ... |
m s−2 |
| Angular acceleration Angular acceleration Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :... |
s−2 |
| jerk | m s−3 |
| "Angular jerk" | s−3 |
| specific energy Specific energy Specific energy is defined as the energy per unit mass. Common metric units are J/kg. It is an intensive property. Contrast this with energy, which is an extensive property. There are two main types of specific energy: potential energy and specific kinetic energy. Others are the gray and sievert,... |
m2 s−2 |
| absorbed dose rate | m2 s−3 |
| moment of inertia Moment of inertia In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation... |
kg m2 |
| momentum Momentum In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object... |
kg m s−1 |
| angular momentum Angular momentum In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system... |
kg m2 s−1 |
| force Force In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform... |
kg m s−2 |
| torque Torque Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist.... |
kg m2 s−2 |
| energy Energy In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems... |
kg m2 s−2 |
| power Power (physics) In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit... |
kg m2 s−3 |
| pressure Pressure Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :... and energy density Energy density Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored... |
kg m−1 s−2 |
| surface tension Surface tension Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface... |
kg s−2 |
| Spring constant | kg s−2 |
| irradiance Irradiance Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter... and energy flux Energy flux Energy flux is the rate of transfer of energy through a surface. The quantity is defined in two different ways, depending on the context:# Rate of energy transfer per unit area... |
kg s−3 |
| kinematic viscosity | m2 s−1 |
| dynamic viscosity | kg m−1 s−1 |
| Density Density The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight... (mass density) |
kg m−3 |
| Density Density The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight... (weight density) |
kg m−2 s−2 |
| Number density Number density In physics, astronomy, and chemistry, number density is an intensive quantity used to describe the degree of concentration of countable objects in the three-dimensional physical space... |
m−3 |
| Action Action (physics) In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is... |
kg m2 s−1 |
The position of a point particle
Point particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
is defined with respect to an arbitrary fixed reference point, O, in space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
, usually accompanied by a coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
, with the reference point located at the origin of the coordinate system. It is defined as the vector r from O to the particle
Particle
A particle is, generally, a small localized object to which can be ascribed physical properties. It may also refer to:In chemistry:* Colloidal particle, part of a one-phase system of two or more components where the particles aren't individually visible.In physics:* Subatomic particle, which may be...
. In general, the point particle need not be stationary relative to O, so r is a function of t, the time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
elapsed since an arbitrary initial time. In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval between any given pair of events is the same for all observers. In addition to relying on absolute time, classical mechanics assumes Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
for the structure of space.
Velocity and speed
The velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, or the rate of change
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
of position with time, is defined as the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the position with respect to time or
-
.
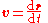In classical mechanics, velocities are directly additive and subtractive. For example, if one car traveling East at 60 km/h passes another car traveling East at 50 km/h, then from the perspective of the slower car, the faster car is traveling east at 60 − 50 = 10 km/h. Whereas, from the perspective of the faster car, the slower car is moving 10 km/h to the West. Velocities are directly additive as vector quantities; they must be dealt with using vector analysis.
Mathematically, if the velocity of the first object in the previous discussion is denoted by the vector and the velocity of the second object by the vector , where u is the speed of the first object, v is the speed of the second object, and d and e are unit vectors in the directions of motion of each particle respectively, then the velocity of the first object as seen by the second object is
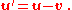
Similarly,
When both objects are moving in the same direction, this equation can be simplified to
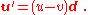
Or, by ignoring direction, the difference can be given in terms of speed only:
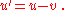
Acceleration
The accelerationAcceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
, or rate of change of velocity, is the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the velocity with respect to time (the second derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the position with respect to time) or
Acceleration can arise from a change with time of the magnitude of the velocity or of the direction of the velocity or both. If only the magnitude v of the velocity decreases, this is sometimes referred to as deceleration, but generally any change in the velocity with time, including deceleration, is simply referred to as acceleration.
Frames of reference
While the position and velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
and acceleration of a particle
Particle
A particle is, generally, a small localized object to which can be ascribed physical properties. It may also refer to:In chemistry:* Colloidal particle, part of a one-phase system of two or more components where the particles aren't individually visible.In physics:* Subatomic particle, which may be...
can be referred to any observer
Observer (special relativity)
The term observer in special relativity refers most commonly to an inertial reference frame. Less often it may refer to an arbitrary non-inertial reference frame; in particular, a Rindler frame is sometimes called an "accelerating observer". In such cases an inertial reference frame may be called...
in any state of motion, classical mechanics assumes the existence of a special family of reference frames
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
in terms of which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames. An inertial frame is such that when an object without any force interactions(an idealized situation) is viewed from it, it will appear either to be at rest or in a state of uniform motion in a straight line. This is the fundamental definition of an inertial frame. They are characterized by the requirement that all forces entering the observer's physical law
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
s originate in identifiable sources (charges, gravitational bodies, and so forth). A non-inertial reference frame is one accelerating with respect to an inertial one, and in such a non-inertial frame a particle is subject to acceleration by fictitious force
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
s that enter the equations of motion solely as a result of its accelerated motion, and do not originate in identifiable sources. These fictitious forces are in addition to the real forces recognized in an inertial frame. A key concept of inertial frames is the method for identifying them. For practical purposes, reference frames that are unaccelerated with respect to the distant stars
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
are regarded as good approximations to inertial frames.
Consider two reference frames S and S' . For observers in each of the reference frames an event has space-time coordinates of (x,y,z,t) in frame S and (x′,y′,z′,t′) in frame S′. Assuming time is measured the same in all reference frames, and if we require x = x when t = 0, then the relation between the space-time coordinates of the same event observed from the reference frames S′ and S, which are moving at a relative velocity of u in the x direction is:
- x′ = x − ut
- y′ = y
- z′ = z
- t′ = t
This set of formulas defines a group transformation known as the Galilean transformation
Galilean transformation
The Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. This is the passive transformation point of view...
(informally, the Galilean transform). This group is a limiting case of the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
used in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. The limiting case applies when the velocity u is very small compared to c, the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
The transformations have the following consequences:
- v′ = v − u (the velocity v′ of a particle from the perspective of S′ is slower by u than its velocity v from the perspective of S)
- a′ = a (the acceleration of a particle is the same in any inertial reference frame)
- F′ = F (the force on a particle is the same in any inertial reference frame)
- the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
is not a constant in classical mechanics, nor does the special position given to the speed of light in relativistic mechanicsRelativistic MechanicsRelativistic mechanics refers to any form of mechanics compatible with either theories of Special Relativity and General Relativity. It is a non-quantum mechanics of a system of particles or of a fluid in cases where some of the velocities are comparable to the speed of light.Special relativity...
have a counterpart in classical mechanics.
For some problems, it is convenient to use rotating coordinates (reference frames). Thereby one can either keep a mapping to a convenient inertial frame, or introduce additionally a fictitious centrifugal force and Coriolis force.
Forces; Newton's second law
NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
was the first to mathematically express the relationship between force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
. Some physicists interpret Newton's second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
as a definition of force and mass, while others consider it to be a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":
The quantity mv is called the (canonical) momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
. The net force on a particle is thus equal to rate change of momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of the particle with time. Since the definition of acceleration is a = dv/dt, the second law can be written in the simplified and more familiar form:
So long as the force acting on a particle is known, Newton's second law is sufficient to describe the motion of a particle. Once independent relations for each force acting on a particle are available, they can be substituted into Newton's second law to obtain an ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
, which is called the equation of motion.
As an example, assume that friction is the only force acting on the particle, and that it may be modeled as a function of the velocity of the particle, for example:
where λ is a positive constant. Then the equation of motion is
This can be integrated
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
to obtain
where v0 is the initial velocity. This means that the velocity of this particle decays exponentially to zero as time progresses. In this case, an equivalent viewpoint is that the kinetic energy of the particle is absorbed by friction (which converts it to heat energy in accordance with the conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
), slowing it down. This expression can be further integrated to obtain the position r of the particle as a function of time.
Important forces include the gravitational force and the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
for electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
. In addition, Newton's third law can sometimes be used to deduce the forces acting on a particle: if it is known that particle A exerts a force F on another particle B, it follows that B must exert an equal and opposite reaction force, −F, on A. The strong form of Newton's third law requires that F and −F act along the line connecting A and B, while the weak form does not. Illustrations of the weak form of Newton's third law are often found for magnetic forces.
Work and energy
If a constant force F is applied to a particle that achieves a displacement Δr,The displacement Δr is the difference of the particle's initial and final positions: Δr = rfinal − rinitial. the work done by the force is defined as the scalar product of the force and displacement vectors:
More generally, if the force varies as a function of position as the particle moves from r1 to r2 along a path C, the work done on the particle is given by the line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
If the work done in moving the particle from r1 to r2 is the same no matter what path is taken, the force is said to be conservative
Conservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
. Gravity is a conservative force, as is the force due to an idealized spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
, as given by Hooke's law
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
. The force due to friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
is non-conservative.
The kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
Ek of a particle of mass m travelling at speed v is given by
For extended objects composed of many particles, the kinetic energy of the composite body is the sum of the kinetic energies of the particles.
The work-energy theorem states that for a particle of constant mass m the total work W done on the particle from position r1 to r2 is equal to the change in kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
Ek of the particle:
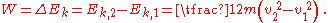
Conservative forces can be expressed as the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar function, known as the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
and denoted Ep:
If all the forces acting on a particle are conservative, and Ep is the total potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
(which is defined as a work of involved forces to rearrange mutual positions of bodies), obtained by summing the potential energies corresponding to each force
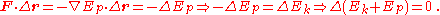
This result is known as conservation of energy and states that the total energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
,
is constant in time. It is often useful, because many commonly encountered forces are conservative.
Beyond Newton's Laws
Classical mechanics also includes descriptions of the complex motions of extended non-pointlike objects. Euler's lawsEuler's laws
Euler's laws of motion, formulated by Leonhard Euler about 50 years after Isaac Newton formulated his laws about the motion of particles, extends them to rigid body motion.-Euler's first law:...
provide extensions to Newton's laws in this area. The concepts of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
rely on the same calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
used to describe one-dimensional motion. The rocket equation extends the notion of rate of change of an object's momentum to include the effects of an object "losing mass".
There are two important alternative formulations of classical mechanics: Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
and Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
. These, and other modern formulations, usually bypass the concept of "force", instead referring to other physical quantities, such as energy, for describing mechanical systems.
The expressions given above for momentum and kinetic energy are only valid when there is no significant electromagnetic contribution. In electromagnetism, Newton's second law for current-carrying wires breaks down unless one includes the electromagnetic field contribution to the momentum of the system as expressed by the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
divided by c2, where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in free space.
History
Some Greek philosophersGreek philosophy
Ancient Greek philosophy arose in the 6th century BCE and continued through the Hellenistic period, at which point Ancient Greece was incorporated in the Roman Empire...
of antiquity, among them Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
, founder of Aristotelian physics
Aristotelian physics
Aristotelian Physics the natural sciences, are described in the works of the Greek philosopher Aristotle . In the Physics, Aristotle established general principles of change that govern all natural bodies; both living and inanimate, celestial and terrestrial—including all motion, change in respect...
, may have been the first to maintain the idea that "everything happens for a reason" and that theoretical principles can assist in the understanding of nature. While to a modern reader, many of these preserved ideas come forth as eminently reasonable, there is a conspicuous lack of both mathematical theory
Theory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
and controlled experiment
Experiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
, as we know it. These both turned out to be decisive factors in forming modern science, and they started out with classical mechanics.
The medieval “science of weights” (i.e., mechanics) owes much of its importance to the work of Jordanus de Nemore. In the Elementa super demonstrationem ponderum, he introduces the concept of “positional gravity” and the use of component forces.
Astronomia nova
The Astronomia nova is a book, published in 1609, that contains the results of the astronomer Johannes Kepler's ten-year long investigation of the motion of Mars...
published in 1609. He concluded, based on Tycho Brahe
Tycho Brahe
Tycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
's observations of the orbit of Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
, that the orbits were ellipses. This break with ancient thought
Ancient philosophy
This page lists some links to ancient philosophy. In Western philosophy, the spread of Christianity through the Roman Empire marked the ending of Hellenistic philosophy and ushered in the beginnings of Medieval philosophy, whereas in Eastern philosophy, the spread of Islam through the Arab Empire...
was happening around the same time that Galilei
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
was proposing abstract mathematical laws for the motion of objects. He may (or may not) have performed the famous experiment of dropping two cannon balls of different weights from the tower of Pisa
Leaning Tower of Pisa
The Leaning Tower of Pisa or simply the Tower of Pisa is the campanile, or freestanding bell tower, of the cathedral of the Italian city of Pisa...
, showing that they both hit the ground at the same time. The reality of this experiment is disputed, but, more importantly, he did carry out quantitative experiments by rolling balls on an inclined plane
Inclined plane
The inclined plane is one of the original six simple machines; as the name suggests, it is a flat surface whose endpoints are at different heights. By moving an object up an inclined plane rather than completely vertical, the amount of force required is reduced, at the expense of increasing the...
. His theory of accelerated motion derived from the results of such experiments, and forms a cornerstone of classical mechanics.
As foundation for his principles of natural philosophy, Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
proposed three laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
: the law of inertia, his second law of acceleration (mentioned above), and the law of action and reaction; and hence laid the foundations for classical mechanics. Both Newton's second and third laws were given proper scientific and mathematical treatment in Newton's Philosophiæ Naturalis Principia Mathematica, which distinguishes them from earlier attempts at explaining similar phenomena, which were either incomplete, incorrect, or given little accurate mathematical expression. Newton also enunciated the principles of conservation of momentum and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. In Mechanics, Newton was also the first to provide the first correct scientific and mathematical formulation of gravity in Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
. The combination of Newton's laws of motion and gravitation provide the fullest and most accurate description of classical mechanics. He demonstrated that these laws apply to everyday objects as well as to celestial objects. In particular, he obtained a theoretical explanation of Kepler's laws of motion of the planets.
Newton previously invented the calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, of mathematics, and used it to perform the mathematical calculations. For acceptability, his book, the Principia
Philosophiae Naturalis Principia Mathematica
Philosophiæ Naturalis Principia Mathematica, Latin for "Mathematical Principles of Natural Philosophy", often referred to as simply the Principia, is a work in three books by Sir Isaac Newton, first published 5 July 1687. Newton also published two further editions, in 1713 and 1726...
, was formulated entirely in terms of the long established geometric methods, which were soon to be eclipsed by his calculus. However it was Leibniz who developed the notation of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
preferred today.
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
, in the form of geometric optics. Even when discovering the so-called Newton's rings
Newton's rings
The phenomenon of Newton's rings, named after Isaac Newton who first studied them in 1717, is an interference pattern caused by the reflection of light between two surfaces - a spherical surface and an adjacent flat surface...
(a wave interference phenomenon) his explanation remained with his own corpuscular theory of light.
After Newton, classical mechanics became a principal field of study in mathematics as well as physics. After Newton there were several re-formulations which progressively allowed a solution to be found to a far greater number of problems. The first notable re-formulation was in 1788 by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
. Lagrangian mechanics was in turn re-formulated in 1833 by William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
.
Some difficulties were discovered in the late 19th century that could only be resolved by more modern physics. Some of these difficulties related to compatibility with electromagnetic theory, and the famous Michelson-Morley experiment
Michelson-Morley experiment
The Michelson–Morley experiment was performed in 1887 by Albert Michelson and Edward Morley at what is now Case Western Reserve University in Cleveland, Ohio. Its results are generally considered to be the first strong evidence against the theory of a luminiferous ether and in favor of special...
. The resolution of these problems led to the special theory of relativity, often included in the term classical mechanics.
A second set of difficulties were related to thermodynamics. When combined with thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, classical mechanics leads to the Gibbs paradox
Gibbs paradox
In statistical mechanics, a semi-classical derivation of the entropy that doesn't take into account the indistinguishability of particles, yields an expression for the entropy which is not extensive...
of classical statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, in which entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
is not a well-defined quantity. Black-body radiation was not explained without the introduction of quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
. As experiments reached the atomic level, classical mechanics failed to explain, even approximately, such basic things as the energy levels and sizes of atoms and the photo-electric effect. The effort at resolving these problems led to the development of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Since the end of the 20th century, the place of classical mechanics in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
has been no longer that of an independent theory. Emphasis has shifted to understanding the fundamental forces of nature as in the Standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
and its more modern extensions into a unified theory of everything
Theory of everything
A theory of everything is a putative theory of theoretical physics that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle....
. Classical mechanics is a theory for the study of the motion of non-quantum mechanical, low-energy particles in weak gravitational fields.
In the 21st century classical mechanics has been extended into the complex domain and complex classical mechanics exhibits behaviours very similar to quantum mechanics.
Limits of validity
Many branches of classical mechanics are simplifications or approximations of more accurate forms; two of the most accurate being general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and relativistic statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. Geometric optics is an approximation to the quantum theory of light
Quantum optics
Quantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
, and does not have a superior "classical" form.
The Newtonian approximation to special relativity
In special relativity, the momentum of a particle is given by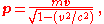where m is the particle's mass, v its velocity, and c is the speed of light.
If v is very small compared to c, v2/c2 is approximately zero, and so
Thus the Newtonian equation is an approximation of the relativistic equation for bodies moving with low speeds compared to the speed of light.
For example, the relativistic cyclotron frequency of a cyclotron
Cyclotron
In technology, a cyclotron is a type of particle accelerator. In physics, the cyclotron frequency or gyrofrequency is the frequency of a charged particle moving perpendicularly to the direction of a uniform magnetic field, i.e. a magnetic field of constant magnitude and direction...
, gyrotron
Gyrotron
Gyrotrons are high powered vacuum tubes which emit millimeter-wave beams by bunching electrons with cyclotron motion in a strong magnetic field. Output frequencies range from about 20 to 250 GHz, covering wavelengths from microwave to the edge of the terahertz gap. Typical output powers range from...
, or high voltage magnetron is given by
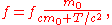
where fc is the classical frequency of an electron (or other charged particle) with kinetic energy T and (rest
Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
) mass m0 circling in a magnetic field.
The (rest) mass of an electron is 511 keV.
So the frequency correction is 1% for a magnetic vacuum tube with a 5.11 kV direct current accelerating voltage.
The classical approximation to quantum mechanics
The ray approximation of classical mechanics breaks down when the de Broglie wavelength is not much smaller than other dimensions of the system. For non-relativistic particles, this wavelength is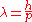where h is Planck's constant and p is the momentum.
Again, this happens with electrons before it happens with heavier particles. For example, the electrons used by Clinton Davisson
Clinton Davisson
Clinton Joseph Davisson , was an American physicist who won the 1937 Nobel Prize in Physics for his discovery of electron diffraction. Davisson shared the Nobel Prize with George Paget Thomson, who independently discovered electron diffraction at about the same time as Davisson.-Early...
and Lester Germer
Lester Germer
Lester Halbert Germer was an American physicist. With Clinton Davisson, he proved the wave-particle duality of matter in the Davisson–Germer experiment, which was important to the development of the electron microscope. These studies supported the theoretical work of De Broglie. He also studied...
in 1927, accelerated by 54 volts, had a wave length of 0.167 nm, which was long enough to exhibit a single diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
side lobe
Side lobe
In antenna engineering, side lobes or sidelobes are the lobes of the far field radiation pattern that are not the main lobe....
when reflecting from the face of a nickel crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
with atomic spacing of 0.215 nm.
With a larger vacuum chamber
Vacuum chamber
A vacuum chamber is a rigid enclosure from which air and other gases are removed by a vacuum pump. The resulting low pressure, commonly referred to as a vacuum, allows researchers to conduct physical experiments or to test mechanical devices which must operate in outer space...
, it would seem relatively easy to increase the angular resolution
Angular resolution
Angular resolution, or spatial resolution, describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object...
from around a radian to a milliradian and see quantum diffraction from the periodic patterns of integrated circuit
Integrated circuit
An integrated circuit or monolithic integrated circuit is an electronic circuit manufactured by the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material...
computer memory.
More practical examples of the failure of classical mechanics on an engineering scale are conduction by quantum tunneling in tunnel diode
Tunnel diode
A tunnel diode or Esaki diode is a type of semiconductor diode which is capable of very fast operation, well into the microwave frequency region, by using quantum mechanical effects....
s and very narrow transistor
Transistor
A transistor is a semiconductor device used to amplify and switch electronic signals and power. It is composed of a semiconductor material with at least three terminals for connection to an external circuit. A voltage or current applied to one pair of the transistor's terminals changes the current...
gates in integrated circuit
Integrated circuit
An integrated circuit or monolithic integrated circuit is an electronic circuit manufactured by the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material...
s.
Classical mechanics is the same extreme high frequency approximation
High frequency approximation
A high frequency approximation for scattering or other wave propagation problems, in physics or engineering, is an approximation whose accuracy increases with the size of features on the scatterer or medium relative to the wavelength of the scattered particles.Classical mechanics and geometric...
as geometric optics. It is more often accurate because it describes particles and bodies with rest mass. These have more momentum and therefore shorter De Broglie wavelengths than massless particles, such as light, with the same kinetic energies.
Branches
- StaticsStaticsStatics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
, the study of equilibriumMechanical equilibriumA standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
and its relation to forceForceIn physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s - DynamicsAnalytical dynamicsIn classical mechanics, analytical dynamics, or more briefly dynamics, is concerned about the relationship between motion of bodies and its causes, namely the forces acting on the bodies and the properties of the bodies...
, the study of motion and its relation to forces - KinematicsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
, dealing with the implications of observed motions without regard for circumstances causing them
Another division is based on the choice of mathematical formalism:
- Newtonian mechanics
- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
Alternatively, a division can be made by region of application:
- Celestial mechanicsCelestial mechanicsCelestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, relating to starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, planetPlanetA planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s and other celestial bodies - Continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, for materials which are modelled as a continuum, e.g., solidSolidSolid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
s and fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s (i.e., liquidLiquidLiquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s and gasGasGas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es). - Relativistic mechanics (i.e. including the specialSpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and generalGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
theories of relativity), for bodies whose speed is close to the speed of light. - Statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, which provides a framework for relating the microscopic properties of individual atoms and molecules to the macroscopic or bulk thermodynamicThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
properties of materials.
External links
- Crowell, Benjamin. Newtonian Physics (an introductory text, uses algebra with optional sections involving calculus)
- Fitzpatrick, Richard. Classical Mechanics (uses calculus)
- Hoiland, Paul (2004). Preferred Frames of Reference & Relativity
- Horbatsch, Marko, "Classical Mechanics Course Notes".
- Rosu, Haret C., "Classical Mechanics". Physics Education. 1999. [arxiv.org : physics/9909035]
- Schiller, Christoph. Motion Mountain (an introductory text, uses some calculus)
- Shapiro, Joel A. (2003). Classical Mechanics
- Sussman, Gerald Jay & Wisdom, Jack & Mayer,Meinhard E. (2001). Structure and Interpretation of Classical Mechanics
- Tong, David. Classical Dynamics (Cambridge lecture notes on Lagrangian and Hamiltonian formalism)
- Kinematic Models for Design Digital Library (KMODDL)
Movies and photos of hundreds of working mechanical-systems models at Cornell UniversityCornell UniversityCornell University is an Ivy League university located in Ithaca, New York, United States. It is a private land-grant university, receiving annual funding from the State of New York for certain educational missions...
. Also includes an e-book library of classic texts on mechanical design and engineering. - MIT OpenCourseWare 8.01: Classical Mechanics Free videos of actual course lectures with links to lecture notes, assignments and exams.