
Projection (mathematics)
Encyclopedia
Generally speaking, in mathematics
, a projection is a mapping of a set (or of a mathematical structure) which is idempotent, which means that a projection is equal to its composition
with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows. Let p be an idempotent map
from a set E into itself (thus p∘p = IdE) and F = p(E) be the image of p. If we denote by π the map p viewed as a map from E onto F and by i the injection
of F into E, then we have i∘π = IdF. Conversely, i∘π = IdF implies that π∘i is idempotent.
Originally, the notion of projection was introduced in Euclidean geometry
to denotes the projection of the Euclidean space
of dimension three onto a plane in it. The two main projections of this kind are
Various other projections, called projection maps have been defined for the need of cartography. The 3D projection
s are also at the basis of the theory of perspective
.
The need of unifying the two kinds of projections and of defining the image by a central projection of any point different of the center of projection are at the origin of projective geometry
.
The original notion of projection has been extended or generalized to various mathematical situations, frequently, but not always, related to geometry, for example:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a projection is a mapping of a set (or of a mathematical structure) which is idempotent, which means that a projection is equal to its composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows. Let p be an idempotent map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from a set E into itself (thus p∘p = IdE) and F = p(E) be the image of p. If we denote by π the map p viewed as a map from E onto F and by i the injection
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
of F into E, then we have i∘π = IdF. Conversely, i∘π = IdF implies that π∘i is idempotent.
Originally, the notion of projection was introduced in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
to denotes the projection of the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of dimension three onto a plane in it. The two main projections of this kind are
- The projection from a point onto a plane or central projection: If C is the point, called center of projection, the projection of a point P different of C is the intersection with the plane of the line CP. The point C and the points P such that the line CP is parallel to the plane do not have any image by the projection.
- The projection onto a plane parallel to a direction D: The image of a point P is the intersection with the plane of the line parallel to D passing through P.
Various other projections, called projection maps have been defined for the need of cartography. The 3D projection
3D projection
3D projection is any method of mapping three-dimensional points to a two-dimensional plane. As most current methods for displaying graphical data are based on planar two-dimensional media, the use of this type of projection is widespread, especially in computer graphics, engineering and drafting.-...
s are also at the basis of the theory of perspective
Perspective (graphical)
Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...
.
The need of unifying the two kinds of projections and of defining the image by a central projection of any point different of the center of projection are at the origin of projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
The original notion of projection has been extended or generalized to various mathematical situations, frequently, but not always, related to geometry, for example:
- In set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
:- An operation typified by the j th projection map, written projj , that takes an element x = (x1, ..., xj , ..., xk) of the cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
X1 × … × Xj × … × Xk to the value projj (x) = xj . This map is always surjective. - A mapping that takes an element to its equivalence class under a given equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
is known as the canonical projection. - The evaluation map sends a function f to the value f(x) for a fixed x. The space of functions YX can be identified with the cartesian product
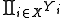 , and the evaluation map is a projection map from the cartesian product.
, and the evaluation map is a projection map from the cartesian product.
- An operation typified by the j th projection map, written projj , that takes an element x = (x1, ..., xj , ..., xk) of the cartesian product
- In category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the above notion of cartesian product of sets can be generalized to arbitrary categoriesCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
. The productProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
of some objects has a canonical projection morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
to each factor. This projection will take many forms in different categories. The projection from the Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of sets, the product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s (which is always surjective and open), or from the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, etc. Although these morphisms are often epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s and even surjective, they do not have to be. - In linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
that remains unchanged if applied twice (p(u) = p(p(u))), in other words, an idempotent operator. For example, the mapping that takes a point (x, y, z) in three dimensions to the point (x, y, 0) in the plane is a projection. This type of projection naturally generalizes to any number of dimensions n for the source and k ≤ n for the target of the mapping. See orthogonal projection, projection (linear algebra)Projection (linear algebra)In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
. In the case of orthogonal projections, the space admits a decomposition as a product, and the projection operator is a projection in that sense as well. - In differential topologyDifferential topologyIn mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, any fiber bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
includes a projection map as part of its definition. Locally at least this map looks like a projection map in the sense of the product topology, and is therefore open and surjective. - In topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a retract is a continuous map r: X → X which restricts to the identity map on its image. This satisfies a similar idempotency condition r2 = r and can be considered a generalization of the projection map. A retract which is homotopic to the identity is known as a deformation retractDeformation retractIn topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
. This term is also used in category theory to refer to any split epimorphism. - The scalar projection (or resolute) of one vector onto another.

