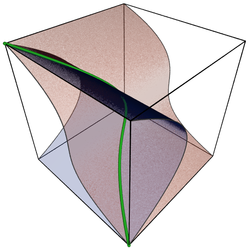
Algebraic variety - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, an algebraic variety is the set of solutions of a system of polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

equation

Equation

An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

s. Algebraic varieties are one of the central objects of study in algebraic geometry

Algebraic geometry

Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...

. The word "variety" is employed in the sense of a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

, for which cognate

Cognate

In linguistics, cognates are words that have a common etymological origin. This learned term derives from the Latin cognatus . Cognates within the same language are called doublets. Strictly speaking, loanwords from another language are usually not meant by the term, e.g...

s of the word "variety" are used in the Romance languages.

Proven around the year 1800, the fundamental theorem of algebra

Fundamental theorem of algebra

The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...

establishes a link between algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

and geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

by showing that a monic polynomial in one variable with complex coefficients (an algebraic object) is determined by the set of its roots (a geometric object). Building on this result, Hilbert's Nullstellensatz

Hilbert's Nullstellensatz

Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...

provides a fundamental correspondence between ideals

Ideal (ring theory)

In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....

of polynomial ring

Polynomial ring

In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...

s and subsets of affine space

Affine space

In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...

. Using the Nullstellensatz and related results, mathematicians are able to capture the geometric notion of a variety

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

in algebraic terms as well as bring geometry to bear on questions of ring theory

Ring theory

In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...

Formal definitions

Algebraic varieties can be classed into four kinds: affine varieties, quasi-affine varieties, projective varieties, and quasi-projective varieties. There is also the more general notion of an abstract algebraic variety

Abstract algebraic variety

In algebraic geometry, an abstract algebraic variety is an algebraic variety that is defined intrinsically, that is, without an embedding into another variety....

Affine varieties

Let k be an algebraically closed field

Algebraically closed field

In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...

and let Aⁿ be an affine n-space

Affine space

over k. The polynomials ƒ in the ring k[x₁, ..., x_n] can be viewed as k-valued functions on Aⁿ by evaluating ƒ at the points in Aⁿ. For each finitely generated ideal

Ideal (ring theory)

S in k[x₁, ..., x_n], define the zero-locus Z(S) to be the set of points in Aⁿ on which the functions in S simultaneously vanish, that is to say

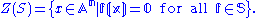
A subset V of Aⁿ is called an affine algebraic set
Algebraic set
In mathematics, an algebraic set over an algebraically closed field K is the set of solutions in Kn of a set of simultaneous equationsand so on up to...

if V = Z(S) for some S. A nonempty affine algebraic set V is called irreducible if it cannot be written as the union of two proper

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

algebraic subsets. An irreducible affine algebraic set is also called an affine variety. (Many authors use the phrase affine variety to refer to any affine algebraic set, irreducible or not; this article will use the stricter definition.)

Affine varieties can be given a natural topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

by declaring the closed set

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

s to be precisely the affine algebraic sets. This topology is called the Zariski topology

Zariski topology

In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...

.

Given a subset V of Aⁿ, we define I(V) to be the ideal of all functions vanishing on V:

For any affine algebraic set V, the coordinate ring or structure ring of V is the quotient

Quotient ring

In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...

of the polynomial ring by this ideal.

Projective varieties

Let k be an algebraically closed field

Algebraically closed field

In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...

and let Pⁿ be a projective n-space

Algebraic geometry of projective spaces

Projective spaces play a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of those spaces.- Homogeneous polynomial ideals:...

over k. Let f ∈ k [x₀, ..., x_n] be a homogeneous polynomial

Homogeneous polynomial

In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...

of degree d. It is not well-defined to evaluate f on points in Pⁿ in homogeneous coordinates

Homogeneous coordinates

In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...

. However, because f is homogeneous, f(λx₀, ..., λx_n) = λ^df(x₀, ..., x_n), so it does make sense to ask whether f vanishes at a point [x₀ : ... : x_n]. For each set S of homogeneous polynomials, define the zero-locus of S to be the set of points in Pⁿ on which the functions in S vanish:

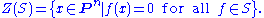
A subset V of Pⁿ is called a projective algebraic set if V = Z(S) for some S. An irreducible projective algebraic set is called a projective variety.

Projective varieties are also equipped with the Zariski topology by declaring all algebraic sets to be closed.

Given a subset V of Pⁿ, let I(V) be the ideal

Ideal (ring theory)

generated by all homogeneous polynomials vanishing on V. For any projective algebraic set V, the coordinate ring of V is the quotient of the polynomial ring by this ideal.

Example 1

Let k be the field of complex numbers C. Let A² be a two dimensional affine space over C. The polynomials f in the ring k[x, y] can be viewed as complex valued functions on A² by evaluating ƒ at the points in A². Let subset S of k[x, y] contain a single element f(x, y):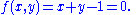

The zero-locus of f(x, y) is the set of points in A² on which this function vanishes: it is the set of all pairs of complex numbers (x,y) such that y = 1 − x, commonly known as a line

Line (geometry)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

. This is the set Z(f):

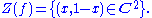
Thus the subset V = Z(f) of A² is an algebraic set. The set V is not an empty set. And it is irreducible as it cannot be written as the union of two proper algebraic subsets. Thus it is an affine algebraic variety.

Example 2

Let again k be the field of complex numbers C. Let A² be a two dimensional affine space over C. The polynomials g in the ring k[x, y] can be viewed as complex valued functions on A² by evaluating g at the points in A². Let subset S of k[x, y] contain a single element g(x, y):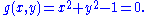

The zero-locus of g(x, y) is the set of points in A² on which this function vanishes, that is the set of points (x,y) such that xx + yy = 1, commonly known as a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

Basic results

An affine algebraic set V is a variety if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

I(V) is a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...

; equivalently, V is a variety if and only if its coordinate ring is an integral domain.
Every nonempty affine algebraic set may be written uniquely as a union of algebraic varieties (where none of the sets in the decomposition are subsets of each other).
Let k[V] be the coordinate ring of the variety V. Then the dimension of V is the transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...

of the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...

of k[V] over k.

Isomorphism of algebraic varieties

Let V₁ and V₂ be algebraic varieties. We say that V₁ and V₂ are isomorphic

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

, and write V₁ ≅ V₂, if there are regular map

Regular function

In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...

s φ : V₁ → V₂ and ψ : V₂ → V₁ such that the compositions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

ψ ° φ and φ ° ψ are the identity maps

Identity function

In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...

on V₁ and V₂ respectively.

Discussion and generalizations

The basic definitions and facts above enable one to do classical algebraic geometry

Algebraic geometry

. To be able to do more — for example, to deal with varieties over fields that are not algebraically closed

Algebraically closed field

In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...

— some foundational changes are required. The modern notion of a variety is considerably more abstract than the one above, though equivalent in the case of varieties over algebraically closed fields. An abstract algebraic variety is a particular kind of scheme

Scheme (mathematics)

In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...

; the generalization to schemes on the geometric side enables an extension of the correspondence described above to a wider class of rings. A scheme is a locally ringed space such that every point has a neighbourhood, which, as a locally ringed space, is isomorphic to a spectrum of a ring

Spectrum of a ring

In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...

. Basically, a variety is a scheme whose structure sheaf is a sheaf

Sheaf (mathematics)

In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...

of k-algebras with the property that the rings R that occur above are all domains and are all finitely generated k-algebras, i.e., quotients of polynomial algebras by prime ideal

Prime ideal

In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...

s.

This definition works over any field k. It allows you to glue affine varieties (along common open sets) without
worrying whether the resulting object can be put into some projective space. This also leads to difficulties since one can introduce somewhat pathological objects, e.g. an affine line with zero doubled. Such objects are usually not considered varieties, and are eliminated by requiring the schemes underlying a variety to be separated. (Strictly speaking, there is also a third condition, namely, that one needs only finitely many affine patches in the definition above.)

Some modern researchers also remove the restriction on a variety having integral domain affine charts, and when speaking of a variety simply mean that the affine charts have trivial nilradical.

A complete variety is a variety such that any map from an open subset of a nonsingular curve

Algebraic curve

In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...

into it can be extended uniquely to the whole curve. Every projective variety is complete, but not vice versa.

These varieties have been called 'varieties in the sense of Serre', since Serre

Jean-Pierre Serre

Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...

's foundational paper FAC on sheaf cohomology

Sheaf cohomology

In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...

was written for them. They remain typical objects to start studying in algebraic geometry, even if more general objects are also used in an auxiliary way.

One way that leads to generalisations is to allow reducible algebraic sets (and fields k that aren't algebraically closed), so the rings R may not be integral domains. A more significant modification is to allow nilpotent

Nilpotent

In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....

s in the sheaf of rings. A nilpotent in a field must be 0: these if allowed in coordinate rings aren't seen as coordinate functions.

From the categorical

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

point of view, nilpotents must be allowed, in order to have finite limits of varieties (to get fiber products). Geometrically this says that fibres of good mappings may have 'infinitesimal' structure. In the theory of scheme

Scheme (mathematics)

s of Grothendieck

Alexander Grothendieck

Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...

these points are all reconciled: but the general scheme is far from having the immediate geometric content of a variety.

There are further generalizations called algebraic space

Algebraic space

In mathematics, an algebraic space is a generalization of the schemes of algebraic geometry introduced by Michael Artin for use in deformation theory...

s and stacks.

Algebraic manifolds

An algebraic manifold is an algebraic variety which is also an m-dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

, and hence every sufficiently small local patch is isomorphic to k^m. Equivalently, the variety is smooth

Smooth function

In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...

(free from singular points

Singular point of an algebraic variety

In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...

). When k is the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, R, algebraic manifolds are called Nash manifolds. Algebraic manifolds can be defined as the zero set of a finite collection of analytic algebraic functions. Projective algebraic manifolds are an equivalent definition for projective varieties. The Riemann sphere

Riemann sphere

In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...

is one example.

Formal definitions

Affine varieties

Projective varieties

Example 1

Example 2

Basic results

Isomorphism of algebraic varieties

Discussion and generalizations

Algebraic manifolds

See also