
Laplace operator
Encyclopedia
In mathematics
the Laplace operator or Laplacian is a differential operator
given by the divergence
of the gradient
of a function
on Euclidean space
. It is usually denoted by the symbols ∇·∇, ∇2 or Δ. The Laplacian Δƒ(p) of a function ƒ at a point p, up to a constant depending on the dimension, is the rate at which the average value of ƒ over spheres centered at p, deviates from ƒ(p) as the radius of the sphere grows. In a Cartesian coordinate system
, the Laplacian is given by sum of all the (unmixed) second partial derivative
s of the function. In other coordinate systems such as cylindrical and spherical coordinates, the Laplacian also has a useful form.
The Laplace operator is named after the French
mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics
, where the operator gives a constant multiple of the mass density when it is applied to a given gravitational potential. Solutions of the equation Δƒ = 0, now called Laplace's equation
, are the so-called harmonic function
s, and represent the possible gravitational fields in free space.
It occurs in the differential equations that describe many physical phenomena, such as electric
and gravitational potentials, the diffusion equation for heat
and fluid flow
, wave propagation
, and quantum mechanics
. The Laplacian represents the flux density
of the gradient flow of a function. For instance, the net rate at which a chemical dissolved in a fluid moves toward or away from some point is proportional to the Laplacian of the chemical concentration at that point; expressed symbolically, the resulting equation is the diffusion equation. For these reasons, it is extensively used in the sciences for modelling all kinds of physical phenomena. The Laplacian is the simplest elliptic operator
, and is at the core of Hodge theory
as well as the results of de Rham cohomology
. In image processing
and computer vision
, the Laplacian operator has been used for various tasks such as blob
and edge detection
.
, defined as the divergence
(∇·) of the gradient
(∇ƒ). Thus if ƒ is a twice-differentiable
real-valued function, then the Laplacian of ƒ is defined by
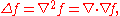 (1)
(1)
Equivalently, the Laplacian of ƒ is the sum of all the unmixed second partial derivative
s in the Cartesian coordinates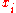 :
:
 (2)
(2)
As a second-order differential operator, the Laplace operator maps Ck-functions to Ck−2-functions for k ≥ 2. The expression (1) (or equivalently (2)) defines an operator , or more generally an operator for any open set
Ω.
theory of diffusion
, the Laplace operator (via Laplace's equation
) arises naturally in the mathematical description of equilibrium. Specifically, if u is the density at equilibrium of some quantity such as a chemical concentration, then the net flux of u through the boundary of any smooth region V is zero, provided there is no source or sink within V:

where n is the outward unit normal to the boundary of V. By the divergence theorem
,

Since this holds for all smooth regions V, it can be shown that this implies
The left-hand side of this equation is the Laplace operator. The Laplace operator itself has a physical interpretation for non-equilibrium diffusion as the extent to which a point represents a source or sink of chemical concentration, in a sense made precise by the diffusion equation.
This is a consequence of Gauss's law
. Indeed, if V is any smooth region, then by Gauss's law the flux of the electrostatic field E is equal to the charge enclosed (in appropriate units):

where the first equality uses the fact that the electrostatic field is the gradient of the electrostatic potential. The divergence theorem now gives
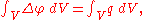
and since this holds for all regions V, follows.
The same approach implies that the Laplacian of the gravitational potential is the mass distribution
. Often the charge (or mass) distribution are given, and the associated potential is unknown. Finding the potential function subject to suitable boundary conditions is equivalent to solving Poisson's equation
.
 in a region U are functions that make the Dirichlet energy
in a region U are functions that make the Dirichlet energy
functional
stationary
:
To see this, suppose
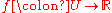 is a function, and
is a function, and
 is a function that vanishes on the
is a function that vanishes on the
boundary of U. Then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Laplace operator or Laplacian is a differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
given by the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. It is usually denoted by the symbols ∇·∇, ∇2 or Δ. The Laplacian Δƒ(p) of a function ƒ at a point p, up to a constant depending on the dimension, is the rate at which the average value of ƒ over spheres centered at p, deviates from ƒ(p) as the radius of the sphere grows. In a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, the Laplacian is given by sum of all the (unmixed) second partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of the function. In other coordinate systems such as cylindrical and spherical coordinates, the Laplacian also has a useful form.
The Laplace operator is named after the French
French people
The French are a nation that share a common French culture and speak the French language as a mother tongue. Historically, the French population are descended from peoples of Celtic, Latin and Germanic origin, and are today a mixture of several ethnic groups...
mathematician Pierre-Simon de Laplace (1749–1827), who first applied the operator to the study of celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, where the operator gives a constant multiple of the mass density when it is applied to a given gravitational potential. Solutions of the equation Δƒ = 0, now called Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
, are the so-called harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s, and represent the possible gravitational fields in free space.
It occurs in the differential equations that describe many physical phenomena, such as electric
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and gravitational potentials, the diffusion equation for heat
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
and fluid flow
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, wave propagation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. The Laplacian represents the flux density
Flux density
-Formal Statement:The flux density is simply defined as the amount of flux passing through a unit-area. -Mathematical Statement:The flux density would essentially be the number of field lines passing through a defined unit-area...
of the gradient flow of a function. For instance, the net rate at which a chemical dissolved in a fluid moves toward or away from some point is proportional to the Laplacian of the chemical concentration at that point; expressed symbolically, the resulting equation is the diffusion equation. For these reasons, it is extensively used in the sciences for modelling all kinds of physical phenomena. The Laplacian is the simplest elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
, and is at the core of Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
as well as the results of de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
. In image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, the Laplacian operator has been used for various tasks such as blob
Blob detection
In the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding...
and edge detection
Edge detection
Edge detection is a fundamental tool in image processing and computer vision, particularly in the areas of feature detection and feature extraction, which aim at identifying points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities...
.
Definition
The Laplace operator is a second order differential operator in the n-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, defined as the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
(∇·) of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
(∇ƒ). Thus if ƒ is a twice-differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
real-valued function, then the Laplacian of ƒ is defined by
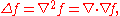 (1)
(1)Equivalently, the Laplacian of ƒ is the sum of all the unmixed second partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s in the Cartesian coordinates
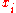 :
: (2)
(2)As a second-order differential operator, the Laplace operator maps Ck-functions to Ck−2-functions for k ≥ 2. The expression (1) (or equivalently (2)) defines an operator , or more generally an operator for any open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
Ω.
Diffusion
In the physicalPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
theory of diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
, the Laplace operator (via Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
) arises naturally in the mathematical description of equilibrium. Specifically, if u is the density at equilibrium of some quantity such as a chemical concentration, then the net flux of u through the boundary of any smooth region V is zero, provided there is no source or sink within V:

where n is the outward unit normal to the boundary of V. By the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
,

Since this holds for all smooth regions V, it can be shown that this implies
The left-hand side of this equation is the Laplace operator. The Laplace operator itself has a physical interpretation for non-equilibrium diffusion as the extent to which a point represents a source or sink of chemical concentration, in a sense made precise by the diffusion equation.
Density associated to a potential
If φ denotes the electrostatic potential associated to a charge distribution q, then the charge distribution itself is given by the Laplacian of φ:This is a consequence of Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
. Indeed, if V is any smooth region, then by Gauss's law the flux of the electrostatic field E is equal to the charge enclosed (in appropriate units):

where the first equality uses the fact that the electrostatic field is the gradient of the electrostatic potential. The divergence theorem now gives
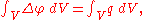
and since this holds for all regions V, follows.
The same approach implies that the Laplacian of the gravitational potential is the mass distribution
Mass distribution
Mass distribution is a term used in physics and mechanics and describes the spatial distribution of mass within a solid body. In principle, it is relevant also for gases or liquids, but on earth their mass distribution is almost homogeneous.-Astronomy:...
. Often the charge (or mass) distribution are given, and the associated potential is unknown. Finding the potential function subject to suitable boundary conditions is equivalent to solving Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
.
Energy minimization
Another motivation for the Laplacian appearing in physics is that solutions to in a region U are functions that make the Dirichlet energy
in a region U are functions that make the Dirichlet energyDirichlet energy
In mathematics, the Dirichlet's energy is a numerical measure of how variable a function is. More abstractly, it is a quadratic functional on the Sobolev space...
functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
stationary
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
:
To see this, suppose
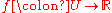 is a function, and
is a function, and is a function that vanishes on the
is a function that vanishes on theboundary of U. Then
-
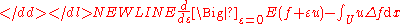
where the last equality follows using Green's first identity.
This calculation shows that if , then
, then
E is stationary around f. Conversely, if E is stationary
around f, then by the fundamental lemma of calculus of variationsFundamental lemma of calculus of variationsIn mathematics, specifically in the calculus of variations, the fundamental lemma in the calculus of variations is a lemma that is typically used to transform a problem from its weak formulation into its strong formulation .-Statement:A function is said to be of class C^k if it is k-times...
by the fundamental lemma of calculus of variationsFundamental lemma of calculus of variationsIn mathematics, specifically in the calculus of variations, the fundamental lemma in the calculus of variations is a lemma that is typically used to transform a problem from its weak formulation into its strong formulation .-Statement:A function is said to be of class C^k if it is k-times...
.
Two dimensions
The Laplace operator in two dimensions is given by
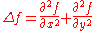
where x and y are the standard Cartesian coordinates of the xy-plane.
In polar coordinates,
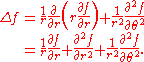
Three dimensions
In three dimensions, it is common to work with the Laplacian in a variety of different coordinate systems.
In Cartesian coordinates,
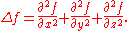
In cylindrical coordinates,
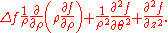
In spherical coordinates:
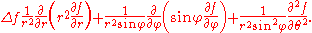
(here θ represents the azimuthal angle and φ the zenith angleZenith AngleZenith Angle can refer to:* In astronomy, the angle made between the surface of the Earth and a line between the observer and the observed * The Zenith Angle is a science fiction novel authored by Bruce Sterling...
or co-latitudeColatitudeIn spherical coordinates, colatitude is the complementary angle of the latitude, i.e. the difference between 90° and the latitude.-Astronomical use:The colatitude is useful in astronomy because it refers to the zenith distance of the celestial poles...
).
In general curvilinear coordinatesCurvilinear coordinatesCurvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
( ):
):
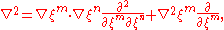
where summation over the repeated indices is implied.
N dimensions
In spherical coordinates in N dimensions, with the parametrization x = rθ ∈ RN with r representing a positive real radius and θ an element of the unit sphereUnit sphereIn mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
SN−1,
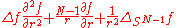
where is the Laplace–Beltrami operator on the (N−1)-sphere, known as the spherical Laplacian. The two radial terms can be equivalently rewritten as
is the Laplace–Beltrami operator on the (N−1)-sphere, known as the spherical Laplacian. The two radial terms can be equivalently rewritten as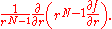
As a consequence, the spherical Laplacian of a function defined on SN−1 ⊂ RN can be computed as the ordinary Laplacian of the function extended to RN\{0} so that it is constant along rays, i.e., homogeneousHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of degree zero.
Spectral theory
The spectrumSpectral theoryIn mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of the Laplace operator consists of all eigenvalues λ for which there is a corresponding eigenfunction ƒ with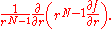
If Ω is a bounded domain in Rn then the eigenfunctions of the Laplacian are an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
for the Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
L2(Ω)Lp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. This result essentially follows from the spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
on compactCompact operatorIn functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
self-adjoint operatorSelf-adjoint operatorIn mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s, applied to the inverse of the Laplacian (which is compact, by the Poincaré inequalityPoincaré inequalityIn mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great...
and Kondrakov embedding theorem). It can also be shown that the eigenfunctions are infinitely differentiable functions. More generally, these results hold for the Laplace–Beltrami operator on any compact Riemannian manifold with boundary, or indeed for the Dirichlet eigenvalue problem of any elliptic operatorElliptic operatorIn the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
with smooth coefficients on a bounded domain. When Ω is the n-sphere, the eigenfunctions of the Laplacian are the well-known spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
.
Laplace–Beltrami operator
The Laplacian also can be generalized to an elliptic operator called the Laplace–Beltrami operator defined on a Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. The d'Alembert operator generalizes to a hyperbolic operator on pseudo-Riemannian manifoldPseudo-Riemannian manifoldIn differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
s. The Laplace–Beltrami operator, when applied to a function, is the traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the function's HessianHessian matrixIn mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
:
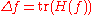
where the trace is taken with respect to the inverse of the metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. The Laplace–Beltrami operator also can be generalized to an operator (also called the Laplace–Beltrami operator) which operates on tensor fieldTensor fieldIn mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
s, by a similar formula.
Another generalization of the Laplace operator that is available on pseudo-Riemannian manifolds uses the exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, in terms of which the Laplacian is expressed as
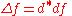
Here d∗ is the codifferential, which can also be expressed using the Hodge dualHodge dualIn mathematics, the Hodge star operator or Hodge dual is a significant linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented inner product space.-Dimensions and algebra:...
. More generally, the Laplacian is defined on differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s α by
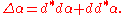
This is known as the Laplace–de Rham operator, which is related Laplace–Beltrami operator by the Weitzenböck identityWeitzenbock identityIn mathematics, in particular in differential geometry, mathematical physics, and representation theory a Weitzenböck identity expresses a relationship between two second-order elliptic operators on a manifold with the same leading symbol...
.
D'Alembertian
The Laplacian can be generalized in certain ways to non-Euclidean spaces, where it may be ellipticElliptic operatorIn the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
, hyperbolic, or ultrahyperbolic.
In the Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
the Laplace–Beltrami operator becomes the d'Alembert operatorD'Alembert operatorIn special relativity, electromagnetism and wave theory, the d'Alembert operator , also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert...
or d'Alembertian:
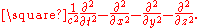
It is the generalisation of the Laplace operator in the sense that it is the differential operator which is invariant under the isometry groupIsometry groupIn mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of the underlying space and it reduces to the Laplace operator if restricted to time independent functions. Note that the overall sign of the metric here is chosen such that the spatial parts of the operator admit a negative sign, which is the usual convention in high energy particle physicsParticle physicsParticle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
. The D'Alembert operator is also known as the wave operator, because it is the differential operator appearing in the wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
s and it is also part of the Klein–Gordon equation, which reduces to the wave equation in the massless case.
The additional factor of c in the metric is needed in physics if space and time are measured in different units; a similar factor would be required if, for example, the x direction were measured in meters while the y direction were measured in centimeters. Indeed, theoretical physicists usually work in units such that c=1Natural unitsIn physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
in order to simplify the equation.
See also
- The vector LaplacianVector LaplacianIn mathematics and physics, the vector Laplace operator, denoted by \scriptstyle \nabla^2, named after Pierre-Simon Laplace, is a differential operator defined over a vector field. The vector Laplacian is similar to the scalar Laplacian...
operator, a generalization of the Laplacian to vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s. - The Laplacian in differential geometry.
- The discrete Laplace operatorDiscrete Laplace operatorIn mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
is an analog of the continuous Laplacian, defined on graphs and grids. - The Laplacian is a common operator in image processingImage processingIn electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and computer visionComputer visionComputer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
(see the Laplacian of Gaussian, blob detectorBlob detectionIn the area of computer vision, blob detection refers to visual modules that are aimed at detecting points and/or regions in the image that differ in properties like brightness or color compared to the surrounding...
, and scale spaceScale spaceScale-space theory is a framework for multi-scale signal representation developed by the computer vision, image processing and signal processing communities with complementary motivations from physics and biological vision...
). - The list of formulas in Riemannian geometry contains expressions for the Laplacian in terms of Christoffel symbols.
- Weyl's lemma (Laplace equation)Weyl's lemma (Laplace equation)In mathematics, Weyl's lemma is a result that provides a "very weak" form of the Laplace equation. It is named after the German mathematician Hermann Weyl.-Statement of the lemma:...
- Earnshaw's theoremEarnshaw's theoremEarnshaw's theorem states that a collection of point charges cannot be maintained in a stable stationary equilibrium configuration solely by the electrostatic interaction of the charges. This was first proven by British mathematician Samuel Earnshaw in 1842. It is usually referenced to magnetic...
which shows that stable static gravitational, electrostatic or magnetic suspension is impossible - Other situations in which a laplacian is defined are: analysis on fractalsAnalysis on fractalsAnalysis on fractals or calculus on fractals is a generalization of calculus on smooth manifolds to calculus on fractals.The theory describes dynamical phenomena which occur on objects modelled by fractals....
, time scale calculusTime scale calculusIn mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid discrete–continuous dynamical systems...
and discrete exterior calculusDiscrete exterior calculusIn mathematics, the discrete exterior calculus is the extension of the exterior calculus to discrete spaces including graphs and finite element meshes. DEC methods have proved to be very powerful in improving and analyzing finite element methods: for instance, DEC-based methods allow the use of...
. - Laplacian of Gaussian
- The vector Laplacian



