In geometry

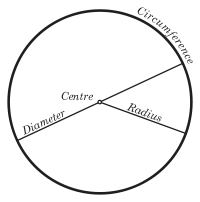
Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a disk (also spelled disc) is the region in a plane bounded by a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

.

A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary. In Cartesian coordinates, the open disk of center 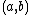and radius R is given by the formula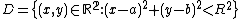
while the closed disk of the same center and radius is given by

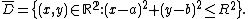
The area of a closed or open disk of radius R is πR² (see π

Pi

' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...

).

The ball

Ball (mathematics)

In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....

is the disk generalised to metric spaces. In context, the term ball may be used instead of disk.

In theoretical physics a disk is a rigid body which is capable of participating in collisions in a two-dimensional gas

Two-dimensional gas

A two-dimensional gas is a collection of N objects which are constrained to move in a planar or other two-dimensional space in a gaseous state. The objects can be: ideal gas elements such as rigid disks undergoing elastic collisions; elementary particles, or any object in physics which obeys laws...

. Usually the disk is considered rigid so that collisions are deemed elastic

Elastic collision

An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter...

.

Topological notions

The open disk and the closed disk are not homeomorphic, since the latter is compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

 and the former is not. However from the viewpoint of algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

 they share many properties: both of them are contractible

Contractible space

In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....

 and so are homotopy equivalent to a single point. This implies that their fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

s are trivial, and all homology groups are trivial except the 0th one, which is isomorphic to Z. The Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

 of a point (and therefore also that of a closed or open disk) is 1.

Every continuous map from the closed disk to itself has at least one fixed point

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

 (we don't require the map to be bijective or even surjective); this is the case n=2 of the Brouwer fixed point theorem

Brouwer fixed point theorem

Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...

. The statement is false for the open disk: consider for example


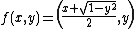
which maps every point of the open unit disk to another point of the open unit disk slightly to the right of the given one.

See also

• Unit disk, a disk with radius one
• Annulus (mathematics)
  Annulus (mathematics)
  In mathematics, an annulus is a ring-shaped geometric figure, or more generally, a term used to name a ring-shaped object. Or, it is the area between two concentric circles...
  
  
• Ball (mathematics)
  Ball (mathematics)
  In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
  
  , the usual term for the 3-dimensional disk
• Disk algebra
  Disk algebra
  In function theory, the disk algebra A is the set of holomorphic functionswhere D is the open unit disk in the complex plane C, f extends to a continuous function on the closure of D...
  
  
• Lentoid
  Lentoid
  Lentoid is a geometric shape of a three-dimensional body, best described as a circle viewed from one direction and a convex lens viewed from an orthogonal direction...
  
  
• Moment of inertia of a uniform disc