
Nash embedding theorem
Encyclopedia
The Nash embedding theorems (or imbedding theorems), named after John Forbes Nash
, state that every Riemannian manifold
can be isometrically embedded
into some Euclidean space
. Isometric means preserving the length of every path. For instance, bending without stretching or tearing a page of paper gives an isometric embedding of the page into Euclidean space because curves drawn on the page retain the same arclength however the page is bent.
The first theorem is for continuously differentiable (C1) embeddings and the second for analytic
embeddings or embeddings that are smooth
of class Ck, 3 ≤ k ≤ ∞. These two theorems are very different from each other; the first one has a very simple proof and is very counterintuitive, while the proof of the second one is very technical but the result is not at all surprising.
The C1 theorem was published in 1954, the Ck-theorem in 1956. The real analytic theorem was first treated by Nash in 1966; his argument was simplified considerably by . (A local version of this result was proved by Élie Cartan
and Maurice Janet in the 1920s.) In the real analytic case, the smoothing operators (see below) in the Nash inverse function argument can be replaced by Cauchy estimates. Nash's proof of the Ck- case was later extrapolated into the h-principle
and Nash–Moser implicit function theorem. A simplified proof of the second Nash embedding theorem was obtained by who reduced the set of nonlinear partial differential equation
s to an elliptic system, to which the contraction mapping theorem could be applied.
C∞-embedding (or immersion
) into Euclidean space Rn, where n ≥ m+1. Then for arbitrary ε > 0 there is an embedding (or immersion) ƒε : Mm → Rn which is in class C1, isometric: for any two vectors v,w ∈ Tx(M) in the tangent space
at x ∈ M,
In particular, as follows from the Whitney embedding theorem, any m-dimensional Riemannian manifold admits an isometric C1-embedding into an arbitrarily small neighborhood in 2m-dimensional Euclidean space.
The theorem was originally proved by John Nash with the condition n ≥ m+2 instead of n ≥ m+1 and generalized by Nicolaas Kuiper
, by a relatively easy trick.
The theorem has many counterintuitive implications. For example, it follows that any closed oriented Riemannian surface can be C1 isometrically embedded into an arbitrarily small ball
in Euclidean 3-space (from the Gauss–Bonnet theorem
, there is no such C2-embedding). And, there exist C1 isometric embeddings of the hyperbolic plane in R3.
dfp is a linear map from the tangent space
TpM to Rn which is compatible with the given inner product
on TpM and the standard dot product of Rn in the following sense:
for all vectors u, v in TpM.
This is an undetermined system of partial differential equation
s (PDEs).
The Nash embedding theorem is a global theorem in the sense that the whole manifold is embedded into Rn.
A local embedding theorem is much simpler and can be proved using the implicit function theorem
of advanced calculus.
The proof of the global embedding theorem relies on Nash's far-reaching generalization of the implicit function theorem, the Nash–Moser theorem and Newton's method with postconditioning.
The basic idea of Nash's solution of the embedding problem is the use of Newton's method
to prove the existence of a solution to the above system of PDEs.
The standard Newton's method fails to converge when applied to the system;
Nash uses smoothing operators defined by convolution
to make the Newton iteration converge: this is Newton's method with postconditioning.
The fact that this technique furnishes a solution is in itself an existence theorem
and of independent interest.
There is also an older method called Kantorovich iteration that uses Newton's method directly (without the introduction of smoothing operators).
John Forbes Nash
John Forbes Nash, Jr. is an American mathematician whose works in game theory, differential geometry, and partial differential equations have provided insight into the forces that govern chance and events inside complex systems in daily life...
, state that every Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
can be isometrically embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
into some Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Isometric means preserving the length of every path. For instance, bending without stretching or tearing a page of paper gives an isometric embedding of the page into Euclidean space because curves drawn on the page retain the same arclength however the page is bent.
The first theorem is for continuously differentiable (C1) embeddings and the second for analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
embeddings or embeddings that are smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
of class Ck, 3 ≤ k ≤ ∞. These two theorems are very different from each other; the first one has a very simple proof and is very counterintuitive, while the proof of the second one is very technical but the result is not at all surprising.
The C1 theorem was published in 1954, the Ck-theorem in 1956. The real analytic theorem was first treated by Nash in 1966; his argument was simplified considerably by . (A local version of this result was proved by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
and Maurice Janet in the 1920s.) In the real analytic case, the smoothing operators (see below) in the Nash inverse function argument can be replaced by Cauchy estimates. Nash's proof of the Ck- case was later extrapolated into the h-principle
H-principle
In mathematics, the homotopy principle is a very general way to solve partial differential equations , and more generally partial differential relations...
and Nash–Moser implicit function theorem. A simplified proof of the second Nash embedding theorem was obtained by who reduced the set of nonlinear partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s to an elliptic system, to which the contraction mapping theorem could be applied.
Nash–Kuiper theorem (C1 embedding theorem)
Theorem. Let (M,g) be a Riemannian manifold and ƒ:Mm → Rn a shortShort map
In the mathematical theory of metric spaces, a metric map is a function between metric spaces that does not increase any distance .These maps are the morphisms in the category of metric spaces, Met ....
C∞-embedding (or immersion
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
) into Euclidean space Rn, where n ≥ m+1. Then for arbitrary ε > 0 there is an embedding (or immersion) ƒε : Mm → Rn which is in class C1, isometric: for any two vectors v,w ∈ Tx(M) in the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at x ∈ M,
-
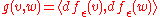 , ε-close to ƒ:
, ε-close to ƒ:- |ƒ(x) − ƒε(x)| < ε for all x ∈ M.
In particular, as follows from the Whitney embedding theorem, any m-dimensional Riemannian manifold admits an isometric C1-embedding into an arbitrarily small neighborhood in 2m-dimensional Euclidean space.
The theorem was originally proved by John Nash with the condition n ≥ m+2 instead of n ≥ m+1 and generalized by Nicolaas Kuiper
Nicolaas Kuiper
Nicolaas Hendrik "Nico" Kuiper was a Dutch mathematician, known for Kuiper's test and proving Kuiper's theorem. He also contributed to the Nash embedding theorem.Kuiper completed his Ph.D...
, by a relatively easy trick.
The theorem has many counterintuitive implications. For example, it follows that any closed oriented Riemannian surface can be C1 isometrically embedded into an arbitrarily small ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
in Euclidean 3-space (from the Gauss–Bonnet theorem
Gauss–Bonnet theorem
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...
, there is no such C2-embedding). And, there exist C1 isometric embeddings of the hyperbolic plane in R3.
Ck embedding theorem
The technical statement is as follows: if M is a given m-dimensional Riemannian manifold (analytic or of class Ck, 3 ≤ k ≤ ∞), then there exists a number n (with n ≤ m(3m+11)/2 if M is a compact manifold, or n ≤ m(m+1)(3m+11)/2 if M is a non-compact manifold) and an injective map f : M → Rn (also analytic or of class Ck) such that for every point p of M, the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
dfp is a linear map from the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
TpM to Rn which is compatible with the given inner product
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
on TpM and the standard dot product of Rn in the following sense:
- ⟨ u, v ⟩ = dfp(u) · dfp(v)
for all vectors u, v in TpM.
This is an undetermined system of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (PDEs).
The Nash embedding theorem is a global theorem in the sense that the whole manifold is embedded into Rn.
A local embedding theorem is much simpler and can be proved using the implicit function theorem
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
of advanced calculus.
The proof of the global embedding theorem relies on Nash's far-reaching generalization of the implicit function theorem, the Nash–Moser theorem and Newton's method with postconditioning.
The basic idea of Nash's solution of the embedding problem is the use of Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
to prove the existence of a solution to the above system of PDEs.
The standard Newton's method fails to converge when applied to the system;
Nash uses smoothing operators defined by convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
to make the Newton iteration converge: this is Newton's method with postconditioning.
The fact that this technique furnishes a solution is in itself an existence theorem
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
and of independent interest.
There is also an older method called Kantorovich iteration that uses Newton's method directly (without the introduction of smoothing operators).

