Rectifiable set
Encyclopedia
In mathematics
, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set. As such, it has many of the desirable properties of smooth manifold
s, including tangent spaces that are defined almost everywhere
. Rectifiable sets are the underlying object of study in geometric measure theory
.
of Euclidean space
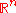is said to be 
-rectifiable set if there exist a countable collection 
of continuously differentiable maps
such that the
-Hausdorff measure
of
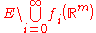
is zero. The backslash here denotes the set difference. Equivalently, the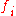
may be taken to be Lipschitz continuous without altering the definition.
A set
is said to be purely 
-unrectifiable if for every (continuous, differentiable) 
, one has
A standard example of a purely-1-unrectifiable set in two dimensions is the cross-product of the Smith-Volterra-Cantor set
times itself.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set. As such, it has many of the desirable properties of smooth manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, including tangent spaces that are defined almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. Rectifiable sets are the underlying object of study in geometric measure theory
Geometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
.
Definition
A subset of Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
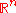is said to be -rectifiable set if there exist a countable collection of continuously differentiable mapssuch that the
-Hausdorff measureHausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
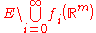
ofis zero. The backslash here denotes the set difference. Equivalently, the
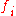may be taken to be Lipschitz continuous without altering the definition.A set
is said to be purely -unrectifiable if for every (continuous, differentiable) , one hasA standard example of a purely-1-unrectifiable set in two dimensions is the cross-product of the Smith-Volterra-Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
times itself.