In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a 3-manifold is a 3-dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

. The topological, piecewise-linear

Piecewise linear manifold

In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...

, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.

Phenomena in three dimensions can be strikingly different from phenomena in other dimensions, and so there is a prevalence of very specialized techniques that do not generalize to dimensions greater than three. This special role has led to the discovery of close connections to a diversity of other fields, such as knot theory

Knot theory

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

, geometric group theory

Geometric group theory

Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...

, hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

, number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

, Teichmüller theory

Teichmüller space

In mathematics, the Teichmüller space TX of a topological surface X, is a space that parameterizes complex structures on X up to the action of homeomorphisms that are isotopic to the identity homeomorphism...

, topological quantum field theory

Topological quantum field theory

A topological quantum field theory is a quantum field theory which computes topological invariants....

, gauge theory

Gauge theory

In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...

, Floer homology

Floer homology

Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...

, and partial differential equations. 3-manifold theory is considered a part of low-dimensional topology

Low-dimensional topology

In mathematics, low-dimensional topology is the branch of topology that studies manifolds of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology.A number of...

 or geometric topology

Geometric topology

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...

.

A key idea in the theory is to study a 3-manifold by considering special surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

s embedded in it. One can choose the surface to be nicely placed in the 3-manifold, which leads to the idea of an incompressible surface

Incompressible surface

In mathematics, an incompressible surface, in intuitive terms, is a surface, embedded in a 3-manifold, which has been simplified as much as possible while remaining "nontrivial" inside the 3-manifold....

 and the theory of Haken manifold

Haken manifold

In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...

s, or one can choose the complementary pieces to be as nice as possible, leading to structures such as Heegaard splitting

Heegaard splitting

In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...

s, which are useful even in the non-Haken case.

Thurston's

William Thurston

William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...

 contributions to the theory allow one to also consider, in many cases, the additional structure given by a particular Thurston model geometry (of which there are eight). The most prevalent geometry is hyperbolic geometry. Using a geometry in addition to special surfaces is often fruitful.

The fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

s of 3-manifolds strongly reflect the geometric and topological information belonging to a 3-manifold. Thus, there is an interplay between group theory

Group theory

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...

 and topological methods.

Important examples of 3-manifolds

• Euclidean 3-space
• 3-sphere
  3-sphere
  In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
  
  
• SO(3) (or 3-dimensional real projective space
  Real projective space
  In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
  
  )
• 3-torus
  Torus
  In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
  
  
• Hyperbolic 3-space
• Poincaré dodecahedral space
• Seifert–Weber space
• Gieseking manifold
  Gieseking manifold
  In mathematics, the Gieseking manifold, is a cusped hyperbolic 3-manifold of finite volume. It is non-orientable and has the smallest volume among non-compact hyperbolic manifolds, having volume approximately 1.01494161...
  
  

Hyperbolic link complements

The following examples are particularly well-known and studied.

• Figure eight knot
  Figure-eight knot (mathematics)
  In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
  
  
• Whitehead link
  Whitehead link
  In knot theory, the Whitehead link, discovered by J.H.C. Whitehead, is one of the most basic links.J.H.C. Whitehead spent much of the 1930s looking for a proof of the Poincaré conjecture...
  
  
• Borromean rings
  Borromean rings
  In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
  
  

Some important classes of 3-manifolds

• Graph manifold
  Graph manifold
  In topology, a graph manifold is a 3-manifold which is obtained by gluing some circle bundles. They were invented and classified by the German topologist Friedhelm Waldhausen in 1967...
  
  
• Haken manifold
  Haken manifold
  In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
  
  
• Homology sphere
  Homology sphere
  In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
  
  s
• Hyperbolic 3-manifold
  Hyperbolic 3-manifold
  A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
  
  
• I-bundle
  I-bundle
  In mathematics, an I-bundle is a fiber bundle whose fiber is an interval and whose base is a manifold. Any kind of interval, open, closed, semi-open, semi-closed, open-bounded, compact, even rays, can be the fiber....
  
  s
• Knot and link complements
• Lens space
  Lens space
  A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
  
  
• Seifert fiber spaces, Circle bundles
• Spherical 3-manifold
  Spherical 3-manifold
  In mathematics, a spherical 3-manifold M is a 3-manifold of the formM=S^3/\Gammawhere \Gamma is a finite subgroup of SO acting freely by rotations on the 3-sphere S^3. All such manifolds are prime, orientable, and closed...
  
  
• Surface bundles over the circle
• Torus bundle
  Torus bundle
  In mathematics, in the sub-field of geometric topology, a torus bundle is a kind of surface bundle over the circle, which in turn are a class of three-manifolds.-Construction:To obtain a torus bundle: let f be an...
  
  

The classes are not necessarily mutually exclusive!

Some important structures on 3-manifolds

• Contact geometry
  Contact geometry
  In mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle and specified by a one-form, both of which satisfy a 'maximum non-degeneracy' condition called 'complete non-integrability'...
  
  
• Essential lamination
• Haken manifold
  Haken manifold
  In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
  
  
• Heegaard splitting
  Heegaard splitting
  In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...
  
  
• Taut foliation
  Taut foliation
  In mathematics, a taut foliation is a codimension 1 foliation of a 3-manifold with the property that there is a single transverse circle intersecting every leaf. By transverse circle, is meant a closed loop that is always transverse to the tangent field of the foliation...
  
  
• Trigenus
  Trigenus
  In low-dimensional topology, the trigenus of a closed 3-manifold is an invariant consisting of an ordered triple . It is obtained by minimizing the genera of three orientable handle bodies — with no intersection between their interiors— which decompose the manifold as far as the...
  
  

Foundational results

Some results are named as conjectures as a result of historical artifacts.

We begin with the purely topological:

• Moise's theorem
  Moise's theorem
  In geometric topology, a branch of mathematics, Moise's theorem, proved by , states that any topological 3-manifold has an essentially unique piecewise-linear structure and smooth structure....
  
   – Every 3-manifold has a triangulation, unique up to common subdivision
  • As corollary, every compact 3-manifold has a Heegaard splitting
    Heegaard splitting
    In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...
    
    .
• Prime decomposition theorem
  Prime decomposition (3-manifold)
  In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique collection of prime 3-manifolds....
  
  
• Kneser–Haken finiteness
• Loop
  Loop theorem
  In mathematics, in the topology of 3-manifolds, the loop theorem is a generalization of Dehn's lemma. The loop theorem was first proven by Christos Papakyriakopoulos in 1956, along with Dehn's lemma and the Sphere theorem....
  
   and sphere
  Sphere theorem (3-manifolds)
  In mathematics, in the topology of 3-manifolds, the sphere theorem of gives conditions for elements of the second homotopy group of a 3-manifold to be represented by embedded spheres.One example is the following:...
  
   theorems
• Annulus
  Annulus theorem
  In mathematics, the annulus theorem states roughly that the region between two well-behaved spheres is an annulus...
  
   and torus theorem
• JSJ decomposition
  JSJ decomposition
  In mathematics, the JSJ decomposition, also known as the toral decomposition, is a topological construct given by the following theorem:The acronym JSJ is for William Jaco, Peter Shalen, and Klaus Johannson...
  
  , also known as the toral decomposition
• Scott core theorem
  Scott core theorem
  In mathematics, the Scott core theorem is a theorem about the finite presentability of fundamental groups of 3-manifolds due to G. Peter Scott,...
  
  
• Lickorish-Wallace theorem
• Waldhausen
  Friedhelm Waldhausen
  Friedhelm Waldhausen is a German mathematician known for his work in algebraic topology.-Academic life:...
  
  's theorems on topological rigidity
• Waldhausen conjecture on Heegaard splittings

Theorems where geometry plays an important role in the proof:

• Smith conjecture
  Smith conjecture
  In mathematics, the Smith conjecture states that if f is a diffeomorphism of the 3-sphere, of finite order then the fixed point set of f cannot be a nontrivial knot....
  
  
• Cyclic surgery theorem
  Cyclic surgery theorem
  In three-dimensional topology, a branch of mathematics, the cyclic surgery theorem states that, for a compact, connected, orientable, irreducible three-manifold M whose boundary is a torus T, if M is not a Seifert-fibered space and r,s are slopes on T such that their Dehn fillings have cyclic...
  
  

Results explicitly linking geometry and topology:

• Thurston's hyperbolic Dehn surgery
  Hyperbolic Dehn surgery
  In mathematics, hyperbolic Dehn surgery is an operation by which one can obtain further hyperbolic 3-manifolds from a given cusped hyperbolic 3-manifold...
  
   theorem
• The Jørgensen–Thurston theorem that the set of finite volumes of hyperbolic 3-manifolds has order type .
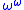• Thurston's hyperbolization theorem
  Hyperbolization theorem
  In geometry, Thurston's geometrization theorem or hyperbolization theorem implies that closed atoroidal Haken manifolds are hyperbolic, and in particular satisfy the Thurston conjecture.-Statement:...
  
   for Haken manifolds
• Tameness conjecture
  Tameness conjecture
  In mathematics, the tameness theorem states that every complete hyperbolic 3-manifold with finitely generated fundamental group is topologically tame, in other words homeomorphic to the interior of a compact 3-manifold....
  
  , also called the Marden conjecture or tame ends conjecture
• Ending lamination conjecture

Important conjectures

Some of these are thought to be solved, as of March 2007. Please see specific articles for more information.

• Poincaré conjecture
  Poincaré conjecture
  In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
  
   — see also Solution of the Poincaré conjecture
• Thurston's geometrization conjecture
• Virtually fibered conjecture
  Virtually fibered conjecture
  In the mathematical subfield of 3-manifolds, the virtually fibered conjecture, formulated by American mathematician William Thurston, states that every closed, irreducible, atoroidal 3-manifold with infinite fundamental group has a finite cover which is a surface bundle over the circle.A 3-manifold...
  
  
• Virtually Haken conjecture
  Virtually Haken conjecture
  In topology, an area of mathematics, the virtually Haken conjecture states that every compact, orientable, irreducible three-dimensional manifold with infinite fundamental group is virtually Haken...
  
  
• Cabling conjecture
• Surface subgroup conjecture
  Surface subgroup conjecture
  In mathematics, the surface subgroup conjecture of Friedhelm Waldhausen states that the fundamental group of every closed, irreducible 3-manifold with infinite fundamental group has a surface subgroup. By "surface subgroup" we mean the fundamental group of a closed surface not the 2-sphere...
  
  
• Simple loop conjecture
• The smallest hyperbolic 3-manifold is the Weeks manifold
  Weeks manifold
  In mathematics, the Weeks manifold, sometimes called the Fomenko–Matveev–Weeks manifold, is a closed hyperbolic 3-manifold obtained by and Dehn surgeries on the Whitehead link. It has volume approximately equal to 0.9427... and showed that it has the smallest volume of any closed orientable...
  
  .
• Lubotzy-Sarnak conjecture on property tau