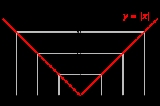
Absolute value
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the absolute value (or modulus) |a| of a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
a is the numerical value of a without regard to its sign
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3. The absolute value of a number may be thought of as its distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
from zero.
Generalizations of the absolute value for real numbers occur in a wide variety of mathematical settings.

