Analytic function
Encyclopedia
In mathematics
, an analytic function is a function
that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not hold generally for real analytic functions. A function is analytic if and only if it is equal to its Taylor series
in some neighborhood of every point.
D in the real line
if for any x0 in D one can write
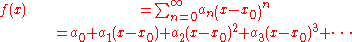
in which the coefficients a0, a1, ... are real numbers and the series
is convergent to ƒ(x) for x in a
neighborhood of x0.
Alternatively, an analytic function is an infinitely differentiable function
such that the Taylor series
at any point x0 in its domain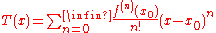
converges to ƒ(x) for x in a neighborhood of x0 (in the mean-square sense). The set of all real analytic functions on a given set D is often denoted by Cω(D).
A function ƒ defined on some subset of the real line is said to be real analytic at a point x if there is a neighborhood D of x on which ƒ is real analytic.
The definition of a complex analytic function is obtained by replacing, in the definitions above, "real" with "complex" and "real line" with "complex plane."
Typical examples of functions that are not analytic are:
, then the following conditions are equivalent.
The real analyticity of a function ƒ at a given point x can be characterized using the FBI transform
.
Complex analytic functions are exactly equivalent to holomorphic function
s, and are thus much more easily characterized.
A polynomial cannot be zero at too many points unless it is the zero polynomial (more precisely, the number of zeros is at most the degree of the polynomial). A similar but weaker statement holds for analytic functions. If the set of zeros of an analytic function ƒ has an accumulation point inside its domain
, then ƒ is zero everywhere on the connected component
containing the accumulation point. In other words, if (rn) is a sequence
of distinct numbers such that ƒ(rn) = 0 for all n and this sequence converges
to a point r in the domain of D, then ƒ is identically zero on the connected component of D containing r.
Also, if all the derivatives of an analytic function at a point are zero, the function is constant on the corresponding connected component.
These statements imply that while analytic functions do have more degrees of freedom
than polynomials, they are still quite rigid.
. In fact there are many such functions, and the space of real analytic functions is a proper subspace of the space of smooth functions.
The situation is quite different when one considers complex analytic functions and complex derivatives. It can be proved that any complex function differentiable (in the complex sense) in an open set is analytic. Consequently, in complex analysis
, the term analytic function is synonymous with holomorphic function
.
According to Liouville's theorem
, any bounded complex analytic function defined on the whole complex plane is constant. The corresponding statement for real analytic functions, with the complex plane replaced by the real line, is clearly false; this is illustrated by
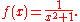
Also, if a complex analytic function is defined in an open ball
around a point x0, its power series expansion at x0 is convergent in the whole ball. This statement for real analytic functions (with open ball meaning an open interval
of the real line rather than an open disk
of the complex plane) is not true in general; the function of the example above gives an example for x0 = 0 and a ball of radius exceeding 1, since the power series diverges for |x| > 1.
Any real analytic function on some open set
on the real line can be extended to a complex analytic function on some open set of the complex plane. However, not every real analytic function defined on the whole real line can be extended to a complex function defined on the whole complex plane. The function ƒ (x) defined in the paragraph above is a counterexample, as it is not defined for x = ±i.
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an analytic function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not hold generally for real analytic functions. A function is analytic if and only if it is equal to its Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
in some neighborhood of every point.
Definitions
Formally, a function ƒ is real analytic on an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
D in the real line
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
if for any x0 in D one can write
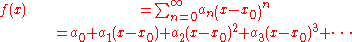
in which the coefficients a0, a1, ... are real numbers and the series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
is convergent to ƒ(x) for x in a
neighborhood of x0.
Alternatively, an analytic function is an infinitely differentiable function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
such that the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
at any point x0 in its domain
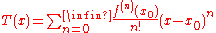
converges to ƒ(x) for x in a neighborhood of x0 (in the mean-square sense). The set of all real analytic functions on a given set D is often denoted by Cω(D).
A function ƒ defined on some subset of the real line is said to be real analytic at a point x if there is a neighborhood D of x on which ƒ is real analytic.
The definition of a complex analytic function is obtained by replacing, in the definitions above, "real" with "complex" and "real line" with "complex plane."
Examples
Most special functions are analytic (at least in some range of the complex plane). Typical examples of analytic functions are:- Any polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
(real or complex) is an analytic function. This is because if a polynomial has degree n, any terms of degree larger than n in its Taylor series expansion must immediately vanish to 0, and so this series will be trivially convergent. Furthermore, every polynomial is its own Maclaurin series.
- The exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
is analytic. Any Taylor series for this function converges not only for x close enough to x0 (as in the definition) but for all values of x (real or complex).
- The trigonometric functionTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s, logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, and the power functionsExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
are analytic on any open set of their domain.
Typical examples of functions that are not analytic are:
- The absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
function when defined on the set of real numbers or complex numbers is not everywhere analytic because it is not differentiable at 0. Piecewise definedPiecewiseOn mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
functions (functions given by different formulas in different regions) are typically not analytic where the pieces meet.
- The complex conjugateComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
function
is not complex analytic, although its restriction to the real line is the identity function and therefore real analytic.
Alternate characterizations
If ƒ is an infinitely differentiable function defined on an open set, then the following conditions are equivalent.- 1) ƒ is real analytic.
- 2) There is a complex analytic extension of ƒ to an open set
which contains 
.
- 3) For every compact set
there exists a constant 
such that for every 
and every non-negative integer k the following estimate holds:
The real analyticity of a function ƒ at a given point x can be characterized using the FBI transform
FBI transform
In mathematics, the FBI transform or Fourier–Bros–Iagolnitzer transform is a non-linear version of the Fourier transform developed by the French mathematical physicists Jacques Bros and Daniel Iagolnitzer in order to characterise the local analyticity of functions on Rn...
.
Complex analytic functions are exactly equivalent to holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s, and are thus much more easily characterized.
Properties of analytic functions
- The sums, products, and compositionsFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of analytic functions are analytic. - The reciprocalMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of an analytic function that is nowhere zero is analytic, as is the inverse of an invertible analytic function whose derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is nowhere zero. (See also the Lagrange inversion theoremLagrange inversion theoremIn mathematical analysis, the Lagrange inversion theorem, also known as the Lagrange-Bürmann formula, gives the Taylor series expansion of the inverse function of an analytic function.-Theorem statement:...
.) - Any analytic function is smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, that is, infinitely differentiable. The converse is not true; in fact, in a certain sense, the analytic functions are sparse compared to all infinitely differentiable functions. - For any open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
Ω ⊆ C, the set A(Ω) of all analytic functions u : Ω → C is a Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
with respect to the uniform convergence on compact sets. The fact that uniform limits on compact sets of analytic functions are analytic is an easy consequence of Morera's theoremMorera's theoremIn complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
. The set
of all boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
analytic functions with the supremum norm is a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
A polynomial cannot be zero at too many points unless it is the zero polynomial (more precisely, the number of zeros is at most the degree of the polynomial). A similar but weaker statement holds for analytic functions. If the set of zeros of an analytic function ƒ has an accumulation point inside its domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
, then ƒ is zero everywhere on the connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
containing the accumulation point. In other words, if (rn) is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of distinct numbers such that ƒ(rn) = 0 for all n and this sequence converges
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to a point r in the domain of D, then ƒ is identically zero on the connected component of D containing r.
Also, if all the derivatives of an analytic function at a point are zero, the function is constant on the corresponding connected component.
These statements imply that while analytic functions do have more degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
than polynomials, they are still quite rigid.
Analyticity and differentiability
As noted above, any analytic function (real or complex) is infinitely differentiable (also known as smooth, or C∞). (Note that this differentiability is in the sense of real variables; compare complex derivatives below.) There exist smooth real functions which are not analytic: see non-analytic smooth functionNon-analytic smooth function
In mathematics, smooth functions and analytic functions are two very important types of functions. One can easily prove that any analytic function of a real argument is smooth...
. In fact there are many such functions, and the space of real analytic functions is a proper subspace of the space of smooth functions.
The situation is quite different when one considers complex analytic functions and complex derivatives. It can be proved that any complex function differentiable (in the complex sense) in an open set is analytic. Consequently, in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, the term analytic function is synonymous with holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
.
Real versus complex analytic functions
Real and complex analytic functions have important differences (one could notice that even from their different relationship with differentiability). Analyticity of complex functions is a more restrictive property, as it has more restrictive necessary conditions and complex analytic functions have more structure than their real-line counterparts.According to Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
, any bounded complex analytic function defined on the whole complex plane is constant. The corresponding statement for real analytic functions, with the complex plane replaced by the real line, is clearly false; this is illustrated by
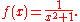
Also, if a complex analytic function is defined in an open ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
around a point x0, its power series expansion at x0 is convergent in the whole ball. This statement for real analytic functions (with open ball meaning an open interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of the real line rather than an open disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
of the complex plane) is not true in general; the function of the example above gives an example for x0 = 0 and a ball of radius exceeding 1, since the power series diverges for |x| > 1.
Any real analytic function on some open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
on the real line can be extended to a complex analytic function on some open set of the complex plane. However, not every real analytic function defined on the whole real line can be extended to a complex function defined on the whole complex plane. The function ƒ (x) defined in the paragraph above is a counterexample, as it is not defined for x = ±i.
Analytic functions of several variables
One can define analytic functions in several variables by means of power series in those variables (see power series). Analytic functions of several variables have some of the same properties as analytic functions of one variable. However, especially for complex analytic functions, new and interesting phenomena show up when working in 2 or more dimensions. For instance, zero sets of complex analytic functions in more than one variable are never discreteDiscrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
.
See also
- Cauchy–Riemann equations
- Holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
- Paley–Wiener theoremPaley–Wiener theoremIn mathematics, a Paley–Wiener theorem is any theorem that relates decay properties of a function or distribution at infinity with analyticity of its Fourier transform. The theorem is named for Raymond Paley and Norbert Wiener . The original theorems did not use the language of distributions,...
- Quasi-analytic function