
Inverse function
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an inverse function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
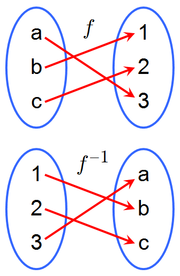
that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ(x)=y, and g(y)=x. More directly, g(ƒ(x))=x, meaning g(x) composed
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
with ƒ(x) leaves x unchanged.
A function ƒ that has an inverse is called invertible; the inverse function is then uniquely determined by ƒ and is denoted by ƒ−1 (read f inverse, not to be confused with exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
).
A relation can be determined to have an inverse if it is a one-to-one function.
Definitions
The word inverse is related to the word invert meaning to reverse, turn upside down, to do the opposite. http://www.thefreedictionary.com/inverse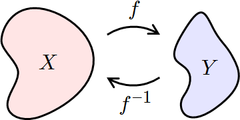
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
, to a set of outputs, the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
. Let ƒ be a function whose domain is the set X, and whose range is the set Y. Then ƒ is invertible if there exists a function g with domain Y and range X, with the property:

If ƒ is invertible, the function g is unique; in other words, there can be at most one function g satisfying this property. That function g is then called the inverse of ƒ, denoted by ƒ−1.
Stated otherwise, a function is invertible if and only if its inverse relation
Inverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
is a function on the range Y, in which case the inverse relation is the inverse function.
Not all functions have an inverse. For this rule to be applicable, each element y ∈ Y must correspond to no more than one x ∈ X; a function ƒ with this property is called one-to-one, or information-preserving, or an injection
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
.
Example: inverse operations that lead to inverse functions
Inverse operations are the opposite of direct variation functions. Direct variation function are based on multiplication; y = kx. The opposite operation of multiplication is division and an inverse variation function is y = k/x.Example: squaring and square root functions
The function ƒ(x) = x2 may or may not be invertible, depending on the domain.If the domain is the real numbers, then each element in Y would correspond to two different elements in X (±x), and therefore ƒ would not be invertible. More precisely, the square of x is not invertible because it is impossible to deduce from its output the sign of its input. Such a function is called non-injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
or information-losing. Notice that neither the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
nor the principal square root function is the inverse of x2 because the first is not single-valued
Single-valued function
A single-valued function is an emphatic term for a mathematical function in the usual sense. That is, each element of the function's domain maps to a single, well-defined element of its range. This contrasts with a general binary relation, which can be viewed as being a multi-valued function...
, and the second returns -x when x is negative.
If the domain consists of the non-negative numbers, then the function is injective and invertible.
Inverses in higher mathematics
The definition given above is commonly adopted in set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. In higher mathematics, the notation

means "ƒ is a function mapping elements of a set X to elements of a set Y". The source, X, is called the domain of ƒ, and the target, Y, is called the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
. The codomain contains the range of ƒ as a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
, and is considered part of the definition of ƒ.
When using codomains, the inverse of a function is required to have domain Y and codomain X. For the inverse to be defined on all of Y, every element of Y must lie in the range of the function ƒ. A function with this property is called onto or a surjection
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
. Thus, a function with a codomain is invertible if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is both injective (one-to-one) and surjective (onto). Such a function is called a one-to-one correspondence or a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
, and has the property that every element corresponds to exactly one element .
Inverses and composition
If ƒ is an invertible function with domain X and range Y, then
This statement is equivalent to the first of the above-given definitions of the inverse, and it becomes equivalent to the second definition if Y coincides with the codomain of ƒ. Using the composition of functions we can rewrite this statement as follows:

where idX is the identity function
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on the set X; that is, the function that leaves X unchanged. In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, this statement is used as the definition of an inverse morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
.
If we think of composition as a kind of multiplication of functions, this identity says that the inverse of a function is analogous to a multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
. This explains the origin of the notation ƒ−1.
Note on notation
The superscript notation for inverses can sometimes be confused with other uses of superscripts, especially when dealing with trigonometric and hyperbolicHyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
functions. To avoid this confusion, the notations ƒ[–1] or with the "-1" above the ƒ are sometimes used.
It is important to realize that ƒ−1(x) is not the same as ƒ(x)−1. In ƒ−1(x), the superscript "−1" is not an exponent. A similar notation is used for iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
s. For example, ƒ2 denotes two iterations of the function ƒ; if , then , which simplifies to . In symbols:
In calculus, ƒ(n), with parentheses, denotes the nth derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function ƒ. For instance:
In trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, for historical reasons, sin2 x usually does mean the square of sin x:

However, the expression sin−1 x usually does not represent the multiplicative inverse to sin x, but the inverse of the sine function applied to x (actually a partial inverse; see below). To avoid confusion, an inverse trigonometric function
Inverse trigonometric function
In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...
is often indicated by the prefix "arc". For instance, the inverse of the sine function is typically called the arcsine function, written as arcsin, which is, like sin, conventionally denoted in roman type
Roman type
In typography, roman is one of the three main kinds of historical type, alongside blackletter and italic. Roman type was modelled from a European scribal manuscript style of the 1400s, based on the pairing of inscriptional capitals used in ancient Rome with Carolingian minuscules developed in the...
and not in italics (note that software libraries of mathematical functions often use the name asin):

The function is the multiplicative inverse to the sine, and is called the cosecant. It is usually denoted csc x:

Hyperbolic functions behave similarly, using the prefix "ar", as in arsinh for the inverse function of sinh, and csch x for the multiplicative inverse of sinh x.
Uniqueness
If an inverse function exists for a given function ƒ, it is unique: it must be the inverse relationInverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
.
Symmetry
There is a symmetry between a function and its inverse. Specifically, if ƒ is an invertible function with domain X and range Y, then its inverse ƒ−1 has domain Y and range X, and the inverse of ƒ−1 is the original function ƒ. In symbols, for ƒ a function with domain X and range Y, and g a function with domain Y and range X:
This follows from the connection between function inverse and relation inverse, because inversion of relations
Inverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
is an involution.
This statement is an obvious consequence of the deduction that for ƒ to be invertible it must be injective (first definition of the inverse) or bijective (second definition). The property of symmetry can be concisely expressed by the following formula:

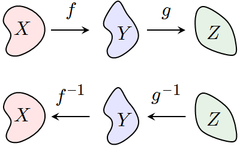

Notice that the order of g and f have been reversed; to undo f followed by g, we must first undo g and then undo f.
For example, let and let . Then the composition is the function that first multiplies by three and then adds five:

To reverse this process, we must first subtract five, and then divide by three:

This is the composition
.
Self-inverses
If X is a set, then the identity functionIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on X is its own inverse:

More generally, a function is equal to its own inverse if and only if the composition is equal to idX. Such a function is called an involution.
Inverses in calculus
Single-variable calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
is primarily concerned with functions that map real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s to real numbers. Such functions are often defined through formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s, such as:

A function ƒ from the real numbers to the real numbers possesses an inverse as long as it is one-to-one, i.e. as long as the graph of has, for each possible y value only one corresponding x value, and thus passes the horizontal line test
Horizontal line test
In mathematics, the horizontal line test is a test used to determine if a function is injective and/or surjective.The lines used for the test are parallel to the x axis....
.
The following table shows several standard functions and their inverses:
| Function ƒ(x) | Inverse ƒ−1(y) | Notes |
|---|---|---|
| x + a | y – a | |
| a – x | a – y | |
| mx | y / m | m ≠ 0 |
| 1 / x | 1 / y | x, y ≠ 0 |
| x2 |  |
x, y ≥ 0 only |
| x3 |  |
no restriction on x and y |
| xp | y1/p (i.e.  ) ) |
x, y ≥ 0 in general, p ≠ 0 |
| ex | ln y | y > 0 |
| ax | loga y | y > 0 and a > 0 |
| trigonometric function Trigonometric function In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle... s |
inverse trigonometric functions | various restrictions (see table below) |
Formula for the inverse
One approach to finding a formula for ƒ−1, if it exists, is to solve the equation for x. For example, if ƒ is the function
then we must solve the equation for x:

Thus the inverse function ƒ−1 is given by the formula

Sometimes the inverse of a function cannot be expressed by a formula with a finite number of terms. For example, if ƒ is the function

then ƒ is one-to-one, and therefore possesses an inverse function ƒ−1. The formula for this inverse has an infinite number of terms:

Graph of the inverse


is the same as the graph of the equation

This is identical to the equation that defines the graph of ƒ, except that the roles of x and y have been reversed. Thus the graph of ƒ−1 can be obtained from the graph of ƒ by switching the positions of the x and y axes. This is equivalent to reflecting
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
the graph across the line
.
Inverses and derivatives
A continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
ƒ is one-to-one (and hence invertible) if and only if it is either strictly increasing or decreasing
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
(with no local maxima or minima
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
). For example, the function

is invertible, since the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is always positive.
If the function ƒ is differentiable, then the inverse ƒ−1 will be differentiable as long as . The derivative of the inverse is given by the inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
:

If we set , then the formula above can be written

This result follows from the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
(see the article on inverse functions and differentiation).
The inverse function theorem can be generalized to functions of several variables. Specifically, a differentiable function is invertible in a neighborhood of a point p as long as the Jacobian matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of ƒ at p is invertible. In this case, the Jacobian of ƒ−1 at ƒ(p) is the matrix inverse of the Jacobian of ƒ at p.
Real-world examples
For example, let ƒ be the function that converts a temperature in degrees Celsius to a temperature in degrees Fahrenheit:
then its inverse function converts degrees Fahrenheit to degrees Celsius:

since

Or, suppose ƒ assigns each child in a family its birth year. An inverse function would output which child was born in a given year. However, if the family has twins (or triplets) then the output cannot be known when the input is the common birth year. As well, if a year is given in which no child was born then a child cannot be named. But if each child was born in a separate year, and if we restrict attention to the three years in which a child was born, then we do have an inverse function. For example,

Partial inverses
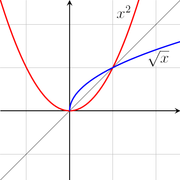

is not one-to-one, since . However, the function becomes one-to-one if we restrict to the domain , in which case

(If we instead restrict to the domain , then the inverse is the negative of the square root of x.) Alternatively, there is no need to restrict the domain if we are content with the inverse being a multivalued function
Multivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
:

Sometimes this multivalued inverse is called the full inverse of ƒ, and the portions (such as √x and −√x) are called branches. The most important branch of a multivalued function (e.g. the positive square root) is called the principal branch, and its value at y is called the principal value of ƒ−1(y).
For a continuous function on the real line, one branch is required between each pair of local extrema. For example, the inverse of a cubic function
Cubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
with a local maximum and a local minimum has three branches (see the picture to the right).
These considerations are particularly important for defining the inverses of trigonometric functions. For example, the sine function is not one-to-one, since

for every real x (and more generally for every integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n). However, the sine is one-to-one on the interval
, and the corresponding partial inverse is called the arcsine. This is considered the principal branch of the inverse sine, so the principal value of the inverse sine is always between –π⁄2 and π⁄2. The following table describes the principal branch of each inverse trigonometric function:
| function | Range of usual principal value Principal value In considering complex multiple-valued functions in complex analysis, the principal values of a function are the values along one chosen branch of that function, so it is single-valued.-Motivation:... |
|---|---|
| sin−1 | –π⁄2 ≤ sin−1(x) ≤ π⁄2 |
| cos−1 | 0 ≤ cos−1(x) ≤ π |
| tan−1 | –π⁄2 < tan−1(x) < π⁄2 |
| cot−1 | 0 < cot−1(x) < π |
| sec−1 | 0 ≤ sec−1(x) ≤ π |
| csc−1 | −π⁄2 ≤ csc−1(x) ≤ π⁄2 |
Left and right inverses
If ƒ: X → Y, a left inverse for ƒ (or retraction of ƒ) is a function such that
That is, the function g satisfies the rule

Thus, g must equal the inverse of ƒ on the range of ƒ, but may take any values for elements of Y not in the range. A function ƒ has a left inverse if and only if it is injective.
A right inverse for ƒ (or section
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of ƒ) is a function such that

That is, the function h satisfies the rule

Thus, h(y) may be any of the elements of X that map to y under ƒ. A function ƒ has a right inverse if and only if it is surjective (though constructing such an inverse in general requires the axiom of choice).
An inverse which is both a left and right inverse must be unique; otherwise not. Likewise, if g is a left inverse for ƒ, then g may or may not be a right inverse for ƒ; and if g is a right inverse for ƒ, then g is not necessarily a left inverse for ƒ. For example let ƒ:R→[0,∞) denote the squaring map, such that ƒ(x)=x2 for all x in R, and let g:[0,∞)→R denote the square root map, such that g(x)=√x for all x≥0. Then ƒ(g(x))=x for all x in [0,∞); that is, g is a right inverse to ƒ. However, g is not a left inverse to ƒ, since, e.g., g(ƒ(-1))=1≠-1.
Preimages
If ƒ: X → Y is any function (not necessarily invertible), the preimage (or inverse image) of an element is the set of all elements of X that map to y:
The preimage of y can be thought of as the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of y under the (multivalued) full inverse of the function f.
Similarly, if S is any subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Y, the preimage of S is the set of all elements of X that map to S:

For example, take a function ƒ: R → R, where ƒ: x → x2. This function is not invertible for reasons discussed above. Yet preimages may be defined for subsets of the codomain:

The preimage of a single element – a singleton set {y} – is sometimes called the fiber of y. When Y is the set of real numbers, it is common to refer to ƒ−1(y) as a level set
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
.
See also
- Inverse trigonometric functionInverse trigonometric functionIn mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions with suitably restricted domains .The notations sin−1, cos−1, etc...
- LogarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
- Inverse function theoremInverse function theoremIn mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
- Inverse functions and differentiation
- Inverse relationInverse relationIn mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
- Inverse elementInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...



