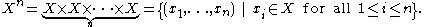Cartesian product
Encyclopedia
In mathematics
, a Cartesian product (or product set) is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets. The Cartesian product is named after René Descartes
, whose formulation of analytic geometry
gave rise to this concept.
The Cartesian product of two sets X (for example the points on an x-axis) and Y (for example the points on a y-axis), denoted X × Y, is the set of all possible ordered pair
s whose first component is a member of X and whose second component is a member of Y (e.g., the whole of the x–y plane):
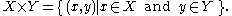
For example, the Cartesian product of the 13-element set of standard playing card ranks {Ace, King, Queen, Jack, 10, 9, 8, 7, 6, 5, 4, 3, 2} and the four-element set of card suits {♠, ♥, ♦, ♣} is the 52-element set of all possible playing cards: ranks × suits = {(Ace, ♠), (King, ♠), ..., (2, ♠), (Ace, ♥), ..., (3, ♣), (2, ♣)}. The corresponding Cartesian product has 52 = 13 × 4 elements. The Cartesian product of the suits × ranks would still be the 52 pairings, but in the opposite order {(♠, Ace), (♠, King), ...}. Ordered pairs (a kind of tuple
) have order, but sets are unordered. The order in which the elements of a set are listed is irrelevant; the deck can be shuffled and it is still the same set of cards.
A Cartesian product of two finite sets can be represented by a table, with one set as the rows and the other as the columns, and forming the ordered pairs, the cells of the table, by choosing the element of the set from the row and the column.
The Cartesian product A × B is not commutative,
because the ordered pair
s are reversed except if at least one condition is satisfied:
For example:
Strictly speaking, the Cartesian product is not associative (unless the above condition occurs).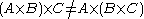
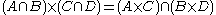
Notice that in most cases the above statement is not true if we replace intersection with union.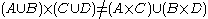
However, for intersection and union it holds for: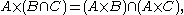
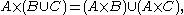
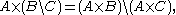
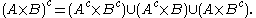
Other properties related with subset
are:
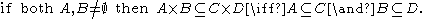
Each element of A is combined with each element of B. Each pair makes up one element of the output set.
The number of values in each pair is equal to the number of sets whose cartesian product is being taken; hence 2 in this case.
The cardinality of the result set is equal to the product of the cardinalities of all the input sets. That is,
and similarly
and so on.
The cardinality of A × B is also infinity
if A or B is an infinite set.
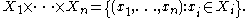
It is a set of n-tuple
s. If tuples are defined as nested ordered pairs, it can be identified to (X1 × ... × Xn-1) × Xn.
An example is the 2-dimensional plane
R2 = R × R where R is the set of real number
s - all points (x,y) where x and y are real numbers (see the Cartesian coordinate system
).
The cartesian power of a set X can be defined as:
An example of this is R3 = R × R × R, with R again the set of real numbers, and more generally Rn.
The n-ary cartesian power of a set X is isomorphic to the space of functions
from an n-element set to X. As a special case, the 0-ary cartesian power of X may be taken to be a singleton set, corresponding to the empty function
with codomain X.
of sets. If I is any index set
, and {Xi | i ∈ I} is a collection of sets indexed by I, then the Cartesian product of the sets in X is defined to be
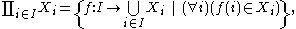
that is, the set of all functions defined on the index set
such that the value of the function at a particular index i is an element of Xi .
For each j in I, the function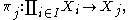
defined by πj(f) = f(j) is called the j -th projection map.
An important case is when the index set is N the natural numbers: this Cartesian product is the set of all infinite sequences with the i -th term in its corresponding set Xi . For example, each element of
can be visualized as a vector with an infinite number of real-number components.
The special case Cartesian exponentiation occurs when all the factors Xi involved in the product are the same set X. In this case,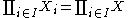
is the set of all functions from I to X. This case is important in the study of cardinal exponentiation.
The definition of finite Cartesian products can be seen as a special case of the definition for infinite products. In this interpretation, an n-tuple can be viewed as a function on {1, 2, ..., n} that takes its value at i to be the i-th element of the tuple (in some settings, this is taken as the very definition of an n-tuple).
Nothing in the definition of an infinite Cartesian product implies that the Cartesian product of nonempty sets must itself be nonempty. This assertion is equivalent to the axiom of choice.
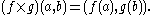
As above this can be extended to tuple
s and infinite collections of functions.
Note that this is different from the standard cartesian product of functions considered as sets.
provides a more general interpretation of the product
of mathematical structures. This is distinct from, although related to, the notion of a Cartesian square in category theory, which is a generalization of the fiber product.
the Cartesian product of two graphs
G and H is the graph denoted by G×H whose vertex set is the (ordinary) Cartesian product V(G)×V(H) and such that two vertices (u,v) and (u′,v′) are adjacent in G×H if and only if u = v and u' is adjacent with v' in H, or u' = v' and u is adjacent with v in G. The Cartesian product of graphs is not a product
in the sense of category theory. Instead, the categorical product is known as the tensor product of graphs
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Cartesian product (or product set) is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets. The Cartesian product is named after René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
, whose formulation of analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
gave rise to this concept.
The Cartesian product of two sets X (for example the points on an x-axis) and Y (for example the points on a y-axis), denoted X × Y, is the set of all possible ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s whose first component is a member of X and whose second component is a member of Y (e.g., the whole of the x–y plane):
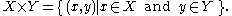
For example, the Cartesian product of the 13-element set of standard playing card ranks {Ace, King, Queen, Jack, 10, 9, 8, 7, 6, 5, 4, 3, 2} and the four-element set of card suits {♠, ♥, ♦, ♣} is the 52-element set of all possible playing cards: ranks × suits = {(Ace, ♠), (King, ♠), ..., (2, ♠), (Ace, ♥), ..., (3, ♣), (2, ♣)}. The corresponding Cartesian product has 52 = 13 × 4 elements. The Cartesian product of the suits × ranks would still be the 52 pairings, but in the opposite order {(♠, Ace), (♠, King), ...}. Ordered pairs (a kind of tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
) have order, but sets are unordered. The order in which the elements of a set are listed is irrelevant; the deck can be shuffled and it is still the same set of cards.
A Cartesian product of two finite sets can be represented by a table, with one set as the rows and the other as the columns, and forming the ordered pairs, the cells of the table, by choosing the element of the set from the row and the column.
Basic properties
Let A, B, C, and D be sets.The Cartesian product A × B is not commutative,

because the ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s are reversed except if at least one condition is satisfied:
- A is equal to B, or
- A or B is an empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
.
For example:
- A = {1,2}; B = {3,4}
- A × B = {1,2} × {3,4} = {(1,3), (1,4), (2,3), (2,4)}
- B × A = {3,4} × {1,2} = {(3,1), (3,2), (4,1), (4,2)}
- A = B = {1,2}
- A × B = B × A = {1,2} × {1,2} = {(1,1), (1,2), (2,1), (2,2)}
- A = {1,2}; B = ∅
- A × B = {1,2} × ∅ = ∅
- B × A = ∅ × {1,2} = ∅
Strictly speaking, the Cartesian product is not associative (unless the above condition occurs).
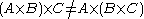
Other set operations
The Cartesian product acts nicely with respect to intersections.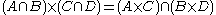
Notice that in most cases the above statement is not true if we replace intersection with union.
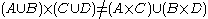
However, for intersection and union it holds for:
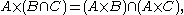
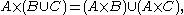
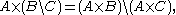
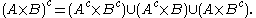
Other properties related with subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
are:

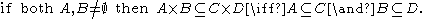
Cardinality
The cardinality of a set is similar to the number of elements of the set. For a simpler example, defining two sets: A = {a, b} and B = {5, 6}. Both set A and set B consist of two elements each. Their Cartesian product, written as A × B, results in a new set which has the following elements:- A × B = {(a,5), (a,6), (b,5), (b,6)}.
Each element of A is combined with each element of B. Each pair makes up one element of the output set.
The number of values in each pair is equal to the number of sets whose cartesian product is being taken; hence 2 in this case.
The cardinality of the result set is equal to the product of the cardinalities of all the input sets. That is,
- |A × B| = |A| · |B|
and similarly
- |A × B × C| = |A| · |B| · |C|
and so on.
The cardinality of A × B is also infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
if A or B is an infinite set.
n-ary product
The Cartesian product can be generalized to the n-ary Cartesian product over n sets X1, ..., Xn: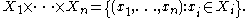
It is a set of n-tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s. If tuples are defined as nested ordered pairs, it can be identified to (X1 × ... × Xn-1) × Xn.
Cartesian square and Cartesian power
The Cartesian square (or binary Cartesian product) of a set X is the Cartesian product X2 = X × X.An example is the 2-dimensional plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
R2 = R × R where R is the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s - all points (x,y) where x and y are real numbers (see the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
).
The cartesian power of a set X can be defined as:
An example of this is R3 = R × R × R, with R again the set of real numbers, and more generally Rn.
The n-ary cartesian power of a set X is isomorphic to the space of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from an n-element set to X. As a special case, the 0-ary cartesian power of X may be taken to be a singleton set, corresponding to the empty function
Empty function
In mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
with codomain X.
Infinite products
It is possible to define the Cartesian product of an arbitrary (possibly infinite) indexed familyIndexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of sets. If I is any index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
, and {Xi | i ∈ I} is a collection of sets indexed by I, then the Cartesian product of the sets in X is defined to be
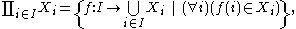
that is, the set of all functions defined on the index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
such that the value of the function at a particular index i is an element of Xi .
For each j in I, the function
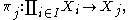
defined by πj(f) = f(j) is called the j -th projection map.
An important case is when the index set is N the natural numbers: this Cartesian product is the set of all infinite sequences with the i -th term in its corresponding set Xi . For example, each element of

can be visualized as a vector with an infinite number of real-number components.
The special case Cartesian exponentiation occurs when all the factors Xi involved in the product are the same set X. In this case,
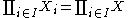
is the set of all functions from I to X. This case is important in the study of cardinal exponentiation.
The definition of finite Cartesian products can be seen as a special case of the definition for infinite products. In this interpretation, an n-tuple can be viewed as a function on {1, 2, ..., n} that takes its value at i to be the i-th element of the tuple (in some settings, this is taken as the very definition of an n-tuple).
Nothing in the definition of an infinite Cartesian product implies that the Cartesian product of nonempty sets must itself be nonempty. This assertion is equivalent to the axiom of choice.
Abbreviated form
If several sets are being multiplied together, e.g. X1, X2, X3, …, then some authors choose to abbreviate the Cartesian product as simply ×Xi.Cartesian product of functions
If f is a function from A to B and g is a function from X to Y, their cartesian product f×g is a function from A×X to B×Y with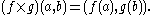
As above this can be extended to tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s and infinite collections of functions.
Note that this is different from the standard cartesian product of functions considered as sets.
Category theory
Although the Cartesian product is traditionally applied to sets, category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
provides a more general interpretation of the product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
of mathematical structures. This is distinct from, although related to, the notion of a Cartesian square in category theory, which is a generalization of the fiber product.
Graph theory
In graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
the Cartesian product of two graphs
Cartesian product of graphs
In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
G and H is the graph denoted by G×H whose vertex set is the (ordinary) Cartesian product V(G)×V(H) and such that two vertices (u,v) and (u′,v′) are adjacent in G×H if and only if u = v and u' is adjacent with v' in H, or u' = v' and u is adjacent with v in G. The Cartesian product of graphs is not a product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
in the sense of category theory. Instead, the categorical product is known as the tensor product of graphs
Tensor product of graphs
In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and...
.
See also
- Exponential objectExponential objectIn mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories...
- Binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
- Empty productEmpty productIn mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
- Product (category theory)Product (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
- Product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
- Finitary relation
- UltraproductUltraproductThe ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
- Product typeProduct typeIn programming languages and type theory, a product of types is another, compounded, type in a structure. The "operands" of the product are types, and the structure of a product type is determined by the fixed order of the operands in the product. An instance of a product type retains the fixed...
- Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
- orders on Rn