In the mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 field of geometric topology

Geometric topology

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...

, a handlebody is a decomposition of a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

 into standard pieces. Handlebodies play an important role in Morse theory

Morse theory

In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...

, cobordism theory and the surgery theory

Surgery theory

In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...

 of high-dimensional manifolds. Handles are used to particularly study 3-manifold

3-manifold

In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...

s.

Handlebodies play a similar role in the study of manifolds as simplicial complex

Simplicial complex

In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...

es and CW complex

CW complex

In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...

es play in homotopy theory, allowing one to analyze a space in terms of individual pieces and their interactions.

n-dimensional handlebodies

If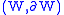 is an -dimensional manifold with boundary, and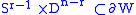

is an embedding, the -dimensional manifold with boundary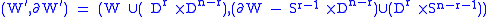

is said to be obtained from

by attaching an -handle.
The boundary is obtained from 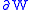by surgery

Surgery theory

In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...

. As trivial examples, note that attaching a 0-handle is just taking a disjoint union with a ball, and that attaching an n-handle
to 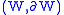is gluing in a ball along any sphere component of 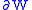. Morse theory

Morse theory

In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...

 was used by Thom

René Thom

René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...

 and Milnor to prove that every manifold (with or without boundary) is a handlebody, meaning that it has an expression as a union of handles. The expression is non-unique: the manipulation of handlebody decompositions is an essential ingredient of the proof of the Smale h-cobordism

H-cobordism

A cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...

 theorem, and its generalization to the s-cobordism theorem. A manifold is called a "k-handlebody" if it is the union of r-handles, for r at most k. This is not the same as the dimension of the manifold. For instance, a 4 dimensional 2-handlebody is a union of 0-handles, 1-handles and 2-handles. Any manifold is an n-handlebody, that is, any manifold is the union of handles. It isn't too hard to see that a manifold is an (n-1)-handlebody if and only if it has non-empty boundary.
Any handlebody decomposition of a manifold defines a CW complex

CW complex

In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...

 decomposition of the manifold, since attaching an r-handle is the same, up to homotopy equivalence, as attaching an r-cell. However, a handlebody decomposition gives more information than just the homotopy type of the manifold. For instance, a handlebody decompostion completely describes the manifold up to homeomorphism. In dimension four, they even describe the smooth structure, as long as the attaching maps are smooth. This is false in higher dimensions; any exotic sphere

Exotic sphere

In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...

 is the union of a 0-handle and an n-handle.

3-dimensional handlebodies

A handlebody can be defined as an orientable 3-manifold-with-boundary containing pairwise disjoint, properly embedded 2-discs such that the manifold resulting from cutting along the discs is a 3-ball. It's instructive to imagine how to reverse this process to get a handlebody. (Sometimes the orientability hypothesis is dropped from this last definition, and one gets a more general kind of handlebody with a non-orientable handle.)

As a bit of notation, the genus of a handlebody is the genus of its boundary

Boundary (topology)

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...

 surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

. Up to

Up to

In mathematics, the phrase "up to x" means "disregarding a possible difference in  x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...

 homeomorphism

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

, there is exactly one handlebody of any non-negative integer genus.

The importance of handlebodies in 3-manifold

3-manifold

In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...

 theory comes from their connection with Heegaard splitting

Heegaard splitting

In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...

s. The importance of handlebodies in geometric group theory

Geometric group theory

Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...

 comes from the fact that their fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

 is free.

A 3-dimensional handlebody is sometimes, particularly in older literature, referred to as a cube with handles.

Examples

Let G be a connected finite graph embedded in Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 of dimension n. Let V be a closed regular neighborhood of G. Then V is an n-dimensional handlebody. The graph G is called a spine of V.

Any genus zero handlebody is homeomorphic to the three-ball B³. A genus one handlebody is homeomorphic to B² × S¹ (where S¹ is the circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

) and is called a solid torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

. All other handlebodies may be obtained by taking the boundary-connected sum

Connected sum

In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...

of a collection of solid tori.