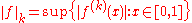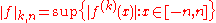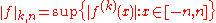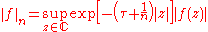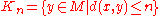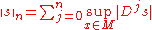Fréchet space
Encyclopedia
In functional analysis
and related areas of mathematics
, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces (normed vector spaces which are complete
with respect to the metric
induced by the norm
). Fréchet spaces, in contrast, are locally convex spaces which are complete with respect to a translation invariant metric.
Even though the topological structure of Fréchet spaces is more complicated than that of Banach spaces due to the lack of a norm, many important results in functional analysis, like the Hahn–Banach theorem
, the open mapping theorem
, and the Banach–Steinhaus theorem, still hold.
Spaces of infinitely differentiable function
s are typical examples of Fréchet spaces.
A topological vector space X is a Fréchet space if and only if
it satisfies the following three properties:
Note that there is no natural notion of distance between two points of a Fréchet space: many different translation-invariant metrics may induce the same topology.
The alternative and somewhat more practical definition is the following: a topological vector space X is a Fréchet space if and only if it satisfies the following three properties:
A sequence (xn) in X converges to x in the Fréchet space defined by a family of semi-norms if and only if it converges to x with respect to each of the given semi-norms.
 is a function from a vector space X to the real numbers satisfying three properties. For all x and y in X and all scalars c,
is a function from a vector space X to the real numbers satisfying three properties. For all x and y in X and all scalars c,


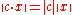
If actually implies that x=0, then
actually implies that x=0, then  is in fact a norm. However, seminorms are useful in that they enable us to construct Fréchet spaces, as follows:
is in fact a norm. However, seminorms are useful in that they enable us to construct Fréchet spaces, as follows:
To construct a Fréchet space, one typically starts with a vector space X and defines a countable family of semi-norms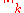 on X with the following two properties:
on X with the following two properties:
Then the topology induced by these seminorms (as explained above) turns X into a Fréchet space; the first property ensures that it is Hausdorff, and the second property ensures that it is complete. A translation-invariant complete metric inducing the same topology on X can then be defined by
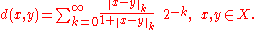
Note that the function u → u / (1+u) maps [0, ∞) monotonically to [0, 1), and so the above definition ensures that d(x, y) is "small" if and only if there exists K "large" such that ||x − y||k is "small" for k = 0, …, K.
is a family of seminorms making C∞(M,V) into a Fréchet space.
Not all vector spaces with complete translation-invariant metrics are Fréchet spaces. An example is the space Lp([0, 1])
with p < 1. This space fails to be locally convex. It is a F-space
.
A closed subspace of a Fréchet space is a Fréchet space. A quotient of a Fréchet space by a closed subspace is a Fréchet space. The direct sum of a finite number of Fréchet spaces is a Fréchet space.
Several important tools of functional analysis which are based on the Baire category theorem
remain true in Fréchet spaces; examples are the closed graph theorem
and the open mapping theorem
.
If X and Y are Fréchet spaces, then the space L(X,Y) consisting of all continuous linear maps from X to Y is not a Fréchet space in any natural manner. This is a major difference between the theory of Banach spaces and that of Fréchet spaces and necessitates a different definition for continuous differentiability of functions defined on Fréchet spaces, the Gâteaux derivative
:
Suppose X and Y are Fréchet spaces, U is an open subset of X, P : U → Y is a function, x ∈ U and h ∈ X. We say that P is differentiable at x in the direction h if the limit
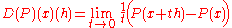
exists. We call P continuously differentiable in U if
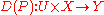
is continuous. Since the product of Fréchet spaces is again a Fréchet space, we can then try to differentiate D(P) and define the higher derivatives of P in this fashion.
The derivative operator P : C∞([0,1]) → C∞([0,1]) defined by P(f) = f′ is itself infinitely differentiable. The first derivative is given by

for any two elements f and h in C∞([0,1]). This is a major advantage of the Fréchet space C∞([0,1]) over the Banach space Ck([0,1]) for finite k.
If P : U → Y is a continuously differentiable function, then the differential equation
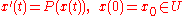
need not have any solutions, and even if does, the solutions need not be unique. This is in stark contrast to the situation in Banach spaces.
The inverse function theorem
is not true in Fréchet spaces; a partial substitute is the Nash–Moser theorem.
Rn), and one can then extend the concept of Lie group
to these manifolds. This is useful because for a given (ordinary) compact C∞ manifold M, the set of all C∞ diffeomorphism
s f : M → M forms a generalized Lie group in this sense, and this Lie group captures the symmetries of M. Some of the relations between Lie algebra
s and Lie groups remain valid in this setting.
s: vector spaces with complete translation-invariant metrics.
LF-space
s are countable inductive limits of Fréchet spaces.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces (normed vector spaces which are complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
with respect to the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
induced by the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
). Fréchet spaces, in contrast, are locally convex spaces which are complete with respect to a translation invariant metric.
Even though the topological structure of Fréchet spaces is more complicated than that of Banach spaces due to the lack of a norm, many important results in functional analysis, like the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
, the open mapping theorem
Open mapping theorem (functional analysis)
In functional analysis, the open mapping theorem, also known as the Banach–Schauder theorem , is a fundamental result which states that if a continuous linear operator between Banach spaces is surjective then it is an open map...
, and the Banach–Steinhaus theorem, still hold.
Spaces of infinitely differentiable function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s are typical examples of Fréchet spaces.
Definitions
Fréchet spaces can be defined in two equivalent ways: the first employs a translation-invariant metric, the second a countable family of semi-norms.A topological vector space X is a Fréchet space if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it satisfies the following three properties:
- it is completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
as a uniform spaceUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between... - it is locally convex
- its topology can be induced by a translation invariant metric, i.e. a metric d : X × X → R such that d(x,y) = d(x+a, y+a) for all a,x,y in X. This means that a subset U of X is openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
if and only if for every u in U there exists an ε > 0 such that {v : d(u,v) < ε} is a subset of U.
Note that there is no natural notion of distance between two points of a Fréchet space: many different translation-invariant metrics may induce the same topology.
The alternative and somewhat more practical definition is the following: a topological vector space X is a Fréchet space if and only if it satisfies the following three properties:
- it is complete as a uniform space
- it is a Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
- its topology may be induced by a countable family of semi-norms ||.||k, k = 0,1,2,... This means that a subset U of X is open if and only if for every u in U there exists K≥0 and ε>0 such that {v : ||u - v||k < ε for all k ≤ K} is a subset of U.
A sequence (xn) in X converges to x in the Fréchet space defined by a family of semi-norms if and only if it converges to x with respect to each of the given semi-norms.
Constructing Fréchet spaces
Recall that a seminorm is a function from a vector space X to the real numbers satisfying three properties. For all x and y in X and all scalars c,
is a function from a vector space X to the real numbers satisfying three properties. For all x and y in X and all scalars c,

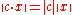
If
 actually implies that x=0, then
actually implies that x=0, then  is in fact a norm. However, seminorms are useful in that they enable us to construct Fréchet spaces, as follows:
is in fact a norm. However, seminorms are useful in that they enable us to construct Fréchet spaces, as follows:To construct a Fréchet space, one typically starts with a vector space X and defines a countable family of semi-norms
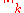 on X with the following two properties:
on X with the following two properties:
- if x ∈ X and
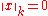 for all k ≥ 0, then x = 0;
for all k ≥ 0, then x = 0; - if (xn) is a sequence in X which is CauchyCauchy sequenceIn mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
with respect to each semi-norm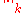 , then there exists x ∈ X such that (xn) converges to x with respect to each semi-norm
, then there exists x ∈ X such that (xn) converges to x with respect to each semi-norm  .
.
Then the topology induced by these seminorms (as explained above) turns X into a Fréchet space; the first property ensures that it is Hausdorff, and the second property ensures that it is complete. A translation-invariant complete metric inducing the same topology on X can then be defined by
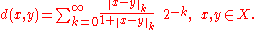
Note that the function u → u / (1+u) maps [0, ∞) monotonically to [0, 1), and so the above definition ensures that d(x, y) is "small" if and only if there exists K "large" such that ||x − y||k is "small" for k = 0, …, K.
Examples
- Every Banach space is a Fréchet space, as the norm induces a translation invariant metric and the space is complete with respect to this metric.
- The vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
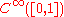 of all infinitely often differentiable functions
of all infinitely often differentiable functions 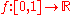 becomes a Fréchet space with the seminorms
becomes a Fréchet space with the seminorms
- for every integer
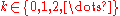 . Here,
. Here, 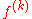 denotes the k-th derivative of ƒ, and
denotes the k-th derivative of ƒ, and 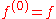 .
.
- In this Fréchet space, a sequence (
 ) of functions convergesLimit (mathematics)In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
) of functions convergesLimit (mathematics)In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
towards the element ƒ of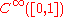 if and only if for every integer
if and only if for every integer  , the sequence (
, the sequence (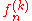 ) converges uniformly towards
) converges uniformly towards 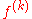 .
.
- The vector space C∞(R) of all infinitely often differentiable functions ƒ : R → R becomes a Fréchet space with the seminorms
- for all integers k, n ≥ 0.
- The vector space Cm(R) of all m-times continuously differentiable functions ƒ : R → R becomes a Fréchet space with the seminorms
- for all integers n ≥ 0 and k=0,...,m.
- Let H be the space of entire (everywhere holomorphic) functions on the complex plane. Then the family of seminorms
- makes H into a Fréchet space.
- Let H be the space of entire (everywhere holomorphic) functions of exponential type
 . Then the family of seminorms
. Then the family of seminorms
- makes H into a Fréchet space.
- If M is a compact C∞-manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
and B is a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, then the set C∞(M,B) of all infinitely-often differentiable functions ƒ : M → B can be turned into a Fréchet space by using as seminorms the suprema of the norms of all partial derivatives. If M is a (not necessarily compact) C∞-manifold which admits a countable sequence Kn of compact subsets, so that every compact subset of M is contained in at least one Kn, then the spaces Cm(M,B) and C∞(M,B) are also Fréchet space in a natural manner.
- In fact, every smooth finite-dimensional manifold M can be made into such a nested union of compact subsets. Equip it with a Riemannian metric g which induces a metric d(x,y), choose x in M, and let
- Let M be a compact C∞-manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
and V a vector bundle over M. Let C∞(M,V) denote the space of smooth sections of V over X. Choose Riemannian metrics and connections, which are guaranteed to exist, on the bundles TX and V. If s is a section, denote its jth covariant derivative by Djs. Then
is a family of seminorms making C∞(M,V) into a Fréchet space.
- The space Rω of all real valued sequences becomes a Fréchet space if we define the k-th semi-norm of a sequence to be the absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the k-th element of the sequence. Convergence in this Fréchet space is equivalent to element-wise convergence.
Not all vector spaces with complete translation-invariant metrics are Fréchet spaces. An example is the space Lp([0, 1])
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
with p < 1. This space fails to be locally convex. It is a F-space
F-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
.
Properties and further notions
If a Fréchet space admits a continuous norm, we can take all the seminorms to be norms by adding the continuous norm to each of them. A Banach space, C∞([a,b]),C∞(X,V) with X compact, and H all admit norms, while Rω and C(R) do not.A closed subspace of a Fréchet space is a Fréchet space. A quotient of a Fréchet space by a closed subspace is a Fréchet space. The direct sum of a finite number of Fréchet spaces is a Fréchet space.
Several important tools of functional analysis which are based on the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
remain true in Fréchet spaces; examples are the closed graph theorem
Closed graph theorem
In mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
and the open mapping theorem
Open mapping theorem
Open mapping theorem may refer to:* Open mapping theorem or Banach–Schauder theorem states that a surjective continuous linear transformation of a Banach space X onto a Banach space Y is an open mapping...
.
If X and Y are Fréchet spaces, then the space L(X,Y) consisting of all continuous linear maps from X to Y is not a Fréchet space in any natural manner. This is a major difference between the theory of Banach spaces and that of Fréchet spaces and necessitates a different definition for continuous differentiability of functions defined on Fréchet spaces, the Gâteaux derivative
Gâteaux derivative
In mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
:
Suppose X and Y are Fréchet spaces, U is an open subset of X, P : U → Y is a function, x ∈ U and h ∈ X. We say that P is differentiable at x in the direction h if the limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
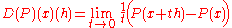
exists. We call P continuously differentiable in U if
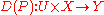
is continuous. Since the product of Fréchet spaces is again a Fréchet space, we can then try to differentiate D(P) and define the higher derivatives of P in this fashion.
The derivative operator P : C∞([0,1]) → C∞([0,1]) defined by P(f) = f′ is itself infinitely differentiable. The first derivative is given by

for any two elements f and h in C∞([0,1]). This is a major advantage of the Fréchet space C∞([0,1]) over the Banach space Ck([0,1]) for finite k.
If P : U → Y is a continuously differentiable function, then the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
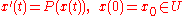
need not have any solutions, and even if does, the solutions need not be unique. This is in stark contrast to the situation in Banach spaces.
The inverse function theorem
Inverse function theorem
In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
is not true in Fréchet spaces; a partial substitute is the Nash–Moser theorem.
Fréchet manifolds and Lie groups
One may define Fréchet manifolds as spaces that "locally look like" Fréchet spaces (just like ordinary manifolds are defined as spaces that locally look like Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn), and one can then extend the concept of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
to these manifolds. This is useful because for a given (ordinary) compact C∞ manifold M, the set of all C∞ diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s f : M → M forms a generalized Lie group in this sense, and this Lie group captures the symmetries of M. Some of the relations between Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s and Lie groups remain valid in this setting.
Generalizations
If we drop the requirement for the space to be locally convex, we obtain F-spaceF-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
s: vector spaces with complete translation-invariant metrics.
LF-space
LF-space
In mathematics, an LF-space is a topological vector space V that is a countable strict inductive limit of Fréchet spaces. This means that for each n there is a subspace V_n such that-Properties:...
s are countable inductive limits of Fréchet spaces.