
Symmetry group
Encyclopedia
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
group of an object (image
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
, signal, etc.) is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of all isometries under which it is invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
with composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
as the operation. It is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of the space concerned.
If not stated otherwise, this article considers symmetry groups in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, but the concept may also be studied in wider contexts; see below.
Introduction
The "objects" may be geometric figures, images, and patterns, such as a wallpaper patternWallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
. The definition can be made more precise by specifying what is meant by image or pattern, e.g., a function of position with values in a set of colors. For symmetry of physical objects, one may also want to take physical composition into account. The group of isometries of space induces a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on objects in it.
The symmetry group is sometimes also called full symmetry group in order to emphasize that it includes the orientation-reversing isometries (like reflections, glide reflection
Glide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
s and improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
s) under which the figure is invariant. The subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of orientation-preserving isometries (i.e. translations, rotations, and compositions of these) which leave the figure invariant is called its proper symmetry group. The proper symmetry group of an object is equal to its full symmetry group if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the object is chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
(and thus there are no orientation-reversing isometries under which it is invariant).
Any symmetry group whose elements have a common fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, which is true for all finite symmetry groups and also for the symmetry groups of bounded figures, can be represented as a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n) by choosing the origin to be a fixed point. The proper symmetry group is a subgroup of the special orthogonal group SO(n) then, and therefore also called rotation group of the figure.
Discrete
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
symmetry groups come in three types: (1) finite point groups, which include only rotations, reflections, inversion and rotoinversion - they are in fact just the finite subgroups of O(n), (2) infinite lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
groups, which include only translations, and (3) infinite space groups which combines elements of both previous types, and may also include extra transformations like screw axis
Screw axis
The screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
and glide reflection
Glide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
. There are also continuous symmetry groups, which contain rotations of arbitrarily small angles or translations of arbitrarily small distances. The group of all symmetries of a sphere O(3)
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
is an example of this, and in general such continuous symmetry
Continuous symmetry
In mathematics, continuous symmetry is an intuitive idea corresponding to the concept of viewing some symmetries as motions, as opposed to e.g. reflection symmetry, which is invariance under a kind of flip from one state to another. It has largely and successfully been formalised in the...
groups are studied as Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. With a categorization of subgroups of the Euclidean group corresponds a categorization of symmetry groups.
Two geometric figures are considered to be of the same symmetry type if their symmetry groups are conjugate subgroups of the Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
E(n) (the isometry group of Rn), where two subgroups H1, H2 of a group G are conjugate, if there exists g ∈ G such that H1=g−1H2g. For example:
- two 3D figures have mirror symmetry, but with respect to different mirror planes.
- two 3D figures have 3-fold rotational symmetry, but with respect to different axes.
- two 2D patterns have translational symmetry, each in one direction; the two translation vectors have the same length but a different direction.
When considering isometry groups, one may restrict oneself to those where for all points the set of images under the isometries is topologically closed. This excludes for example in 1D the group of translations by a rational number. A "figure" with this symmetry group is non-drawable and up to arbitrarily fine detail homogeneous, without being really homogeneous.
One dimension
The isometry groups in 1D where for all points the set of images under the isometries is topologically closed are:- the trivial group C1
- the groups of two elements generated by a reflection in a point; they are isomorphic with C2
- the infinite discrete groups generated by a translation; they are isomorphic with Z
- the infinite discrete groups generated by a translation and a reflection in a point; they are isomorphic with the generalized dihedral group of Z, Dih(Z), also denoted by D∞ (which is a semidirect productSemidirect productIn mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of Z and C2). - the group generated by all translations (isomorphic with R); this group cannot be the symmetry group of a "pattern": it would be homogeneous, hence could also be reflected. However, a uniform 1D vector field has this symmetry group.
- the group generated by all translations and reflections in points; they are isomorphic with the generalized dihedral group of R, Dih(R).
See also symmetry groups in one dimension
Symmetry groups in one dimension
A one-dimensional symmetry group is a mathematical group that describes symmetries in one dimension .A pattern in 1D can be represented as a function f for, say, the color at position x....
.
Two dimensions
Up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
conjugacy the discrete point groups in 2 dimensional space are the following classes:
- cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s C1, C2, C3, C4,... where Cn consists of all rotations about a fixed point by multiples of the angle 360°/n - dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s D1, D2, D3Dihedral group of order 6The smallest non-abelian group has 6 elements. It is a dihedral group with notation D3 and the symmetric group of degree 3, with notation S3....
, D4,... where Dn (of order 2n) consists of the rotations in Cn together with reflections in n axes that pass through the fixed point.
C1 is the trivial group containing only the identity operation, which occurs when the figure has no symmetry at all, for example the letter F. C2 is the symmetry group of the letter Z, C3 that of a triskelion
Triskelion
A triskelion or triskele is a motif consisting of three interlocked spirals, or three bent human legs, or any similar symbol with three protrusions and a threefold rotational symmetry. Both words are from Greek or , "three-legged", from prefix "τρι-" , "three times" + "σκέλος" , "leg"...
, C4 of a swastika
Swastika
The swastika is an equilateral cross with its arms bent at right angles, in either right-facing form in counter clock motion or its mirrored left-facing form in clock motion. Earliest archaeological evidence of swastika-shaped ornaments dates back to the Indus Valley Civilization of Ancient...
, and C5, C6 etc. are the symmetry groups of similar swastika-like figures with five, six etc. arms instead of four.
D1 is the 2-element group containing the identity operation and a single reflection, which occurs when the figure has only a single axis of bilateral symmetry
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
, for example the letter A. D2, which is isomorphic to the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
, is the symmetry group of a non-equilateral rectangle, and D3, D4 etc. are the symmetry groups of the regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s.
The actual symmetry groups in each of these cases have two degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
for the center of rotation, and in the case of the dihedral groups, one more for the positions of the mirrors.
The remaining isometry groups in 2D with a fixed point, where for all points the set of images under the isometries is topologically closed are:
- the special orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
SO(2) consisting of all rotations about a fixed point; it is also called the circle group S1, the multiplicative group of complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1. It is the proper symmetry group of a circle and the continuous equivalent of Cn. There is no figure which has as full symmetry group the circle group, but for a vector field it may apply (see the 3D case below). - the orthogonal group O(2) consisting of all rotations about a fixed point and reflections in any axis through that fixed point. This is the symmetry group of a circle. It is also called Dih(S1) as it is the generalized dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of S1.
For non-bounded figures, the additional isometry groups can include translations; the closed ones are:
- the 7 frieze groupFrieze groupA frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s - the 17 wallpaper groupWallpaper groupA wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s - for each of the symmetry groups in 1D, the combination of all symmetries in that group in one direction, and the group of all translations in the perpendicular direction
- ditto with also reflections in a line in the first direction
Three dimensions
Up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
conjugacy the set of 3D point groups consists of 7 infinite series, and 7 separate ones. In crystallography they are restricted to be compatible with the discrete translation symmetries of a crystal lattice. This crystallographic restriction
Crystallographic restriction theorem
The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...
of the infinite families of general point groups results in 32 crystallographic point groups (27 from the 7 infinite series, and 5 of the 7 others).
The continuous symmetry groups with a fixed point include those of:
- cylindrical symmetry without a symmetry plane perpendicular to the axis, this applies for example often for a bottleBottleA bottle is a rigid container with a neck that is narrower than the body and a "mouth". By contrast, a jar has a relatively large mouth or opening. Bottles are often made of glass, clay, plastic, aluminum or other impervious materials, and typically used to store liquids such as water, milk, soft...
- cylindrical symmetry with a symmetry plane perpendicular to the axis
- spherical symmetry
For objects and scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
s the cylindrical symmetry implies vertical planes of reflection. However, for vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s it does not: in cylindrical coordinates with respect to some axis,
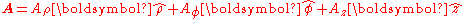 has cylindrical symmetry with respect to the axis if and only if
has cylindrical symmetry with respect to the axis if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
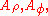 and
and  have this symmetry, i.e., they do not depend on φ. Additionally there is reflectional symmetry if and only if
have this symmetry, i.e., they do not depend on φ. Additionally there is reflectional symmetry if and only if  .
.For spherical symmetry there is no such distinction, it implies planes of reflection.
The continuous symmetry groups without a fixed point include those with a screw axis
Screw axis
The screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
, such as an infinite helix
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
. See also subgroups of the Euclidean group.
Symmetry groups in general
In wider contexts, a symmetry group may be any kind of transformation group, or automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
group. Once we know what kind of mathematical structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
we are concerned with, we should be able to pinpoint what mappings
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
preserve the structure. Conversely, specifying the symmetry can define the structure, or at least clarify what we mean by an invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
, geometric language in which to discuss it; this is one way of looking at the Erlangen programme.
For example, automorphism groups of certain models of finite geometries
Finite geometry
A finite geometry is any geometric system that has only a finite number of points.Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers...
are not "symmetry groups" in the usual sense, although they preserve symmetry. They do this by preserving families of point-sets rather than point-sets (or "objects") themselves.
Like above, the group of automorphisms of space induces a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on objects in it.
For a given geometric figure in a given geometric space, consider the following equivalence relation: two automorphisms of space are equivalent if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the two images of the figure are the same (here "the same" does not mean something like e.g. "the same up to translation and rotation", but it means "exactly the same"). Then the equivalence class of the identity is the symmetry group of the figure, and every equivalence class corresponds to one isomorphic version of the figure.
There is a bijection between every pair of equivalence classes: the inverse of a representative of the first equivalence class, composed with a representative of the second.
In the case of a finite automorphism group of the whole space, its order is the order of the symmetry group of the figure multiplied by the number of isomorphic versions of the figure.
Examples:
- Isometries of the Euclidean plane, the figure is a rectangle: there are infinitely many equivalence classes; each contains 4 isometries.
- The space is a cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
with Euclidean metric; the figures include cubes of the same size as the space, with colors or patterns on the faces; the automorphisms of the space are the 48 isometries; the figure is a cube of which one face has a different color; the figure has a symmetry group of 8 isometries, there are 6 equivalence classes of 8 isometries, for 6 isomorphic versions of the figure.
Compare Lagrange's theorem (group theory)
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
and its proof.
See also
External links
- Overview of the 32 crystallographic point groups - form the first parts (apart from skipping n=5) of the 7 infinite series and 5 of the 7 separate 3D point groups

