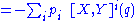Poisson bracket
Encyclopedia
In mathematics
and classical mechanics
, the Poisson bracket is an important binary operation in Hamiltonian mechanics
, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system
. The Poisson bracket also distinguishes a certain class of coordinate-transformations, the so-called
"canonical transformations", which maps canonical coordinate systems into canonical coordinate systems. (A "canonical coordinate system" consists of canonical position/momentum variables, that satisfy canonical Poisson-bracket relations.) Note that the set of possible canonical transformations is always very rich. For instance, often it is possible to choose the Hamiltonian itself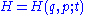 as one of the new canonical momentum coordinates.
as one of the new canonical momentum coordinates.
In a more general sense: the Poisson bracket is used to define a Poisson algebra
, of which the algebra of functions on a Poisson manifold
is a special case. These are all named in honour of Siméon-Denis Poisson.
(also known as Darboux coordinates)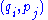 on the phase space
on the phase space
, given two functions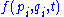 and
and 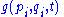 , the Poisson bracket takes the form
, the Poisson bracket takes the form
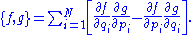
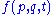 is a function on the manifold. Then one has
is a function on the manifold. Then one has
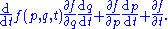
Then, by taking and
and 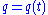 to be solutions to the Hamilton equations
to be solutions to the Hamilton equations  and
and  , one may write
, one may write
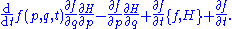
Thus, the time evolution of a function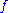 on a symplectic manifold
on a symplectic manifold
can be given as a one-parameter family
of symplectomorphism
s, with the time t being the parameter. Dropping the coordinates, one has
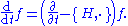
The operator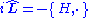 is known as the Liouvillian.
is known as the Liouvillian.
 is a constant of motion. This implies that if
is a constant of motion. This implies that if 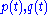 is a trajectory
is a trajectory
or solution to the Hamilton's equations of motion, then one has that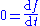 along that trajectory. Then one has
along that trajectory. Then one has
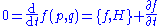
where, as above, the intermediate step follows by applying the equations of motion. This equation is known as the Liouville equation. The content of Liouville's theorem
is that the time evolution of a measure
(or "distribution function
" on the phase space) is given by the above.
In order for a Hamiltonian system to be completely integrable, all of the constants of motion must be in mutual involution.
, that is, a manifold
equipped with a symplectic form: a 2-form
 which is both closed (
which is both closed (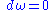 ) and non-degenerate, in the following sense: when viewed as a map
) and non-degenerate, in the following sense: when viewed as a map  ,
,  is invertible to obtain
is invertible to obtain  . Here
. Here  is the exterior derivative
is the exterior derivative
operation intrinsic to the manifold structure of M, and is the interior product or contraction
is the interior product or contraction
operation, which is equivalent to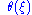 on 1-forms
on 1-forms 
Using the axioms of the exterior calculus, one can derive:

Here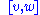 denotes the Lie bracket
denotes the Lie bracket
on smooth vector fields, whose properties essentially define the manifold structure of M.
If v is such that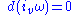 , we may call it
, we may call it  -coclosed (or just coclosed). Similarly, if
-coclosed (or just coclosed). Similarly, if 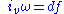 for some function f, we may call v
for some function f, we may call v  -coexact (or just coexact). Given that
-coexact (or just coexact). Given that  , the expression above implies that the Lie bracket of two coclosed vector fields is always a coexact vector field, because when v and w are both coclosed, the only nonzero term in the expression is
, the expression above implies that the Lie bracket of two coclosed vector fields is always a coexact vector field, because when v and w are both coclosed, the only nonzero term in the expression is 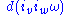 . And because the exterior derivative obeys
. And because the exterior derivative obeys 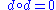 , all coexact vector fields are coclosed; so the Lie bracket is closed both on the space of coclosed vector fields and on the subspace within it consisting of the coexact vector fields. In the language of abstract algebra
, all coexact vector fields are coclosed; so the Lie bracket is closed both on the space of coclosed vector fields and on the subspace within it consisting of the coexact vector fields. In the language of abstract algebra
, the coclosed vector fields form a subalgebra
of the Lie algebra
of smooth vector fields on M, and the coexact vector fields form an algebraic ideal of this subalgebra.
Given the existence of the inverse map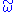 , every smooth real-valued function f on M may be associated with a coexact vector field
, every smooth real-valued function f on M may be associated with a coexact vector field 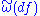 . (Two functions are associated with the same vector field if and only if their difference is in the kernel of d, i. e., constant on each connected component of M.) We therefore define the Poisson bracket on
. (Two functions are associated with the same vector field if and only if their difference is in the kernel of d, i. e., constant on each connected component of M.) We therefore define the Poisson bracket on 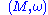 , a bilinear
, a bilinear
operation on differentiable function
s, under which the (smooth) functions form an algebra
(smooth) functions form an algebra
. It is given by:

The skew-symmetry of the Poisson bracket is ensured by the axioms of the exterior calculus and the condition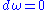 . Because the map
. Because the map 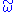 is pointwise linear and skew-symmetric in this sense, some authors associate it with a bivector, which is not an object often encountered in the exterior calculus. In this form it is called the Poisson bivector or the Poisson structure on the symplectic manifold, and the Poisson bracket written simply
is pointwise linear and skew-symmetric in this sense, some authors associate it with a bivector, which is not an object often encountered in the exterior calculus. In this form it is called the Poisson bivector or the Poisson structure on the symplectic manifold, and the Poisson bracket written simply  .
.
The Poisson bracket on smooth functions corresponds to the Lie bracket on coexact vector fields and inherits its properties. It therefore satisfies the Jacobi identity
:
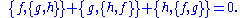
The Poisson bracket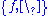 with respect to a particular scalar field f corresponds to the Lie derivative
with respect to a particular scalar field f corresponds to the Lie derivative
with respect to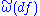 . Consequently, it is a derivation
. Consequently, it is a derivation
; that is, it satisfies Leibniz' law:
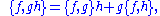
also known as the "Poisson property".
It is a fundamental property of manifolds that the commutator
of the Lie derivative operations with respect to two vector fields is equivalent to the Lie derivative with respect to some vector field, namely, their Lie bracket. The parallel role of the Poisson bracket is apparent from a rearrangement of the Jacobi identity:
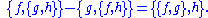
If the Poisson bracket of f and g vanishes ( ), then f and g are said to be in mutual involution, and the operations of taking the Poisson bracket with respect to f and with respect to g commute.
), then f and g are said to be in mutual involution, and the operations of taking the Poisson bracket with respect to f and with respect to g commute.
. This makes the space of smooth function
s on a symplectic manifold
an infinite-dimensional Lie algebra
with the Poisson bracket acting as the Lie bracket
. The corresponding Lie group
is the group of symplectomorphisms of the symplectic manifold (also known as canonical transformation
s).
Given a smooth vector field
X on the tangent bundle
, let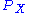 be its conjugate momentum. The conjugate momentum mapping is a Lie algebra
be its conjugate momentum. The conjugate momentum mapping is a Lie algebra
anti-homomorphism from the Poisson bracket to the Lie bracket
:
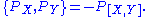
This important result is worth a short proof. Write a vector field X at point q in the configuration space
as

where the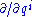 is the local coordinate frame. The conjugate momentum to X has the expression
is the local coordinate frame. The conjugate momentum to X has the expression
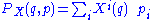
where the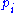 are the momentum functions conjugate to the coordinates. One then has, for a point
are the momentum functions conjugate to the coordinates. One then has, for a point 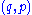 in the phase space
in the phase space
,

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the Poisson bracket is an important binary operation in Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
. The Poisson bracket also distinguishes a certain class of coordinate-transformations, the so-called
"canonical transformations", which maps canonical coordinate systems into canonical coordinate systems. (A "canonical coordinate system" consists of canonical position/momentum variables, that satisfy canonical Poisson-bracket relations.) Note that the set of possible canonical transformations is always very rich. For instance, often it is possible to choose the Hamiltonian itself
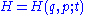 as one of the new canonical momentum coordinates.
as one of the new canonical momentum coordinates.In a more general sense: the Poisson bracket is used to define a Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
, of which the algebra of functions on a Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
is a special case. These are all named in honour of Siméon-Denis Poisson.
Canonical coordinates
In canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
(also known as Darboux coordinates)
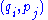 on the phase space
on the phase spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
, given two functions
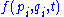 and
and 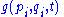 , the Poisson bracket takes the form
, the Poisson bracket takes the form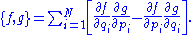
Hamilton's Equations of motion
The Hamilton's equations of motion have an equivalent expression in terms of the Poisson bracket. This may be most directly demonstrated in an explicit coordinate frame. Suppose that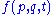 is a function on the manifold. Then one has
is a function on the manifold. Then one has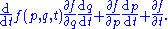
Then, by taking
 and
and 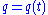 to be solutions to the Hamilton equations
to be solutions to the Hamilton equations  and
and  , one may write
, one may write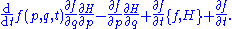
Thus, the time evolution of a function
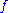 on a symplectic manifold
on a symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
can be given as a one-parameter family
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
of symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
s, with the time t being the parameter. Dropping the coordinates, one has
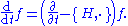
The operator
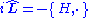 is known as the Liouvillian.
is known as the Liouvillian.Constants of motion
An integrable dynamical system will have constants of motion in addition to the energy. Such constants of motion will commute with the Hamiltonian under the Poisson bracket. Suppose some function is a constant of motion. This implies that if
is a constant of motion. This implies that if 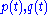 is a trajectory
is a trajectoryTrajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
or solution to the Hamilton's equations of motion, then one has that
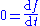 along that trajectory. Then one has
along that trajectory. Then one has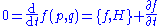
where, as above, the intermediate step follows by applying the equations of motion. This equation is known as the Liouville equation. The content of Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
is that the time evolution of a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
(or "distribution function
Distribution function
In molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
" on the phase space) is given by the above.
In order for a Hamiltonian system to be completely integrable, all of the constants of motion must be in mutual involution.
Definition
Let M be symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
, that is, a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
equipped with a symplectic form: a 2-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
 which is both closed (
which is both closed (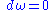 ) and non-degenerate, in the following sense: when viewed as a map
) and non-degenerate, in the following sense: when viewed as a map  ,
,  is invertible to obtain
is invertible to obtain  . Here
. Here  is the exterior derivative
is the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
operation intrinsic to the manifold structure of M, and
 is the interior product or contraction
is the interior product or contractionTensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
operation, which is equivalent to
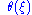 on 1-forms
on 1-forms 
Using the axioms of the exterior calculus, one can derive:

Here
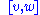 denotes the Lie bracket
denotes the Lie bracketLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
on smooth vector fields, whose properties essentially define the manifold structure of M.
If v is such that
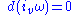 , we may call it
, we may call it  -coclosed (or just coclosed). Similarly, if
-coclosed (or just coclosed). Similarly, if 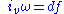 for some function f, we may call v
for some function f, we may call v  -coexact (or just coexact). Given that
-coexact (or just coexact). Given that  , the expression above implies that the Lie bracket of two coclosed vector fields is always a coexact vector field, because when v and w are both coclosed, the only nonzero term in the expression is
, the expression above implies that the Lie bracket of two coclosed vector fields is always a coexact vector field, because when v and w are both coclosed, the only nonzero term in the expression is 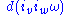 . And because the exterior derivative obeys
. And because the exterior derivative obeys 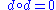 , all coexact vector fields are coclosed; so the Lie bracket is closed both on the space of coclosed vector fields and on the subspace within it consisting of the coexact vector fields. In the language of abstract algebra
, all coexact vector fields are coclosed; so the Lie bracket is closed both on the space of coclosed vector fields and on the subspace within it consisting of the coexact vector fields. In the language of abstract algebraAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the coclosed vector fields form a subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of smooth vector fields on M, and the coexact vector fields form an algebraic ideal of this subalgebra.
Given the existence of the inverse map
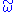 , every smooth real-valued function f on M may be associated with a coexact vector field
, every smooth real-valued function f on M may be associated with a coexact vector field 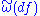 . (Two functions are associated with the same vector field if and only if their difference is in the kernel of d, i. e., constant on each connected component of M.) We therefore define the Poisson bracket on
. (Two functions are associated with the same vector field if and only if their difference is in the kernel of d, i. e., constant on each connected component of M.) We therefore define the Poisson bracket on 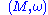 , a bilinear
, a bilinearBilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
operation on differentiable function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s, under which the
 (smooth) functions form an algebra
(smooth) functions form an algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. It is given by:

The skew-symmetry of the Poisson bracket is ensured by the axioms of the exterior calculus and the condition
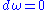 . Because the map
. Because the map 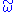 is pointwise linear and skew-symmetric in this sense, some authors associate it with a bivector, which is not an object often encountered in the exterior calculus. In this form it is called the Poisson bivector or the Poisson structure on the symplectic manifold, and the Poisson bracket written simply
is pointwise linear and skew-symmetric in this sense, some authors associate it with a bivector, which is not an object often encountered in the exterior calculus. In this form it is called the Poisson bivector or the Poisson structure on the symplectic manifold, and the Poisson bracket written simply  .
.The Poisson bracket on smooth functions corresponds to the Lie bracket on coexact vector fields and inherits its properties. It therefore satisfies the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
:
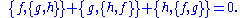
The Poisson bracket
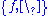 with respect to a particular scalar field f corresponds to the Lie derivative
with respect to a particular scalar field f corresponds to the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
with respect to
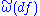 . Consequently, it is a derivation
. Consequently, it is a derivationDerivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
; that is, it satisfies Leibniz' law:
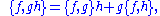
also known as the "Poisson property".
It is a fundamental property of manifolds that the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of the Lie derivative operations with respect to two vector fields is equivalent to the Lie derivative with respect to some vector field, namely, their Lie bracket. The parallel role of the Poisson bracket is apparent from a rearrangement of the Jacobi identity:
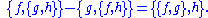
If the Poisson bracket of f and g vanishes (
 ), then f and g are said to be in mutual involution, and the operations of taking the Poisson bracket with respect to f and with respect to g commute.
), then f and g are said to be in mutual involution, and the operations of taking the Poisson bracket with respect to f and with respect to g commute.Lie algebra
The Poisson bracket is skewsymmetric/antisymmetric. (Equivalently, viewed as a binary product operation, it is anticommutative.) It also satisfies the Jacobi identityJacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
. This makes the space of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s on a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
an infinite-dimensional Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
with the Poisson bracket acting as the Lie bracket
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. The corresponding Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is the group of symplectomorphisms of the symplectic manifold (also known as canonical transformation
Canonical transformation
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
s).
Given a smooth vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
X on the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, let
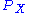 be its conjugate momentum. The conjugate momentum mapping is a Lie algebra
be its conjugate momentum. The conjugate momentum mapping is a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
anti-homomorphism from the Poisson bracket to the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
:
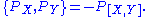
This important result is worth a short proof. Write a vector field X at point q in the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
as

where the
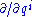 is the local coordinate frame. The conjugate momentum to X has the expression
is the local coordinate frame. The conjugate momentum to X has the expression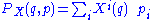
where the
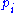 are the momentum functions conjugate to the coordinates. One then has, for a point
are the momentum functions conjugate to the coordinates. One then has, for a point 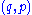 in the phase space
in the phase spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
,

-
-

The above holds for all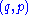 , giving the desired result.
, giving the desired result.
See also
- Poisson algebraPoisson algebraIn mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
- Phase spacePhase spaceIn mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
- Lagrange bracketLagrange bracketLagrange brackets are certain expressions closely related to Poisson brackets that were introduced by Joseph Louis Lagrange in 1808–1810 for the purposes of mathematical formulation of classical mechanics, but unlike the Poisson brackets, have fallen out of use....
- Moyal bracketMoyal bracketIn physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
- Peierls bracketPeierls bracketIn theoretical physics, the Peierls bracket is an equivalent description of the Poisson bracket. It directly follows from the action and does not require the canonical coordinates and their canonical momenta to be defined in advance.The bracket[A,B]...
- Poisson superalgebraPoisson superalgebraIn mathematics, a Poisson superalgebra is a Z2-graded generalization of a Poisson algebra. Specifically, a Poisson superalgebra is an superalgebra A with a Lie superbracket[\cdot,\cdot] : A\otimes A\to A...
- Poisson superbracket
- Dirac bracketDirac bracketThe Dirac bracket is a generalization of the Poisson bracket developed by Paul Dirac to correctly treat systems with second class constraints in Hamiltonian mechanics and canonical quantization. It is an important part of Dirac's development of Hamiltonian mechanics to handle more general Lagrangians...
- CommutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
-
-