
CR manifold
Encyclopedia
In mathematics
, a CR manifold is a differentiable manifold
together with a geometric structure modeled on that of a real hypersurface
in a complex vector space
, or more generally modeled on an edge of a wedge
.
Formally, a CR manifold is a differentiable manifold M together with a preferred complex distribution L, or in other words a subbundle
of the complexified tangent bundle
CTM = TM ⊗ C such that
The bundle L is called a CR structure on the manifold M.
The abbreviation CR stands for Cauchy-Riemann or Complex-Real.
s which are tangent to the hypersurface.
Suppose for instance that M is the hypersurface of C2 given by the equation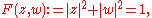
where z and w are the usual complex coordinates on C2. The holomorphic tangent bundle of C2 consists of all linear combinations of the vectors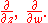
The distribution L on M consists of all combinations of these vectors which are tangent to M. In detail, the tangent vectors must annihilate the defining equation for M, so L consists of complex scalar multiples of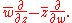
Note that L gives a CR structure on M, for [L,L] = 0 (since L is one-dimensional) and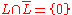 since ∂/∂z and ∂/∂w are linearly independent of their complex conjugates.
since ∂/∂z and ∂/∂w are linearly independent of their complex conjugates.
More generally, suppose that M is a real hypersurface in Cn, with defining equation F(z1, ..., zn) = 0. Then the CR structure L consists of those linear combinations of the basic holomorphic vectors on Cn:
which annihilate the defining function. In this case,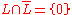 for the same reason as before. Moreover, [L,L] ⊂ L since the commutator of vector fields annihilating F is again a vector field annihilating F.
for the same reason as before. Moreover, [L,L] ⊂ L since the commutator of vector fields annihilating F is again a vector field annihilating F.
Embedded CR manifolds possess some additional structure, though: a Neumann and Dirichlet problem
for the Cauchy-Riemann equations.
This article first treats the geometry of embedded CR manifolds, shows how to defined these structures intrinsically, and then generalizes these to the abstract setting.
Also relevant are the characteristic annihilators from the Dolbeault complex:
The exterior products of these are denoted by the self-evident notation Ω(p,q), and the Dolbeault operator and its complex conjugate map between these spaces via

Furthermore, there is a decomposition of the usual exterior derivative
via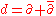 .
.
Suppose that this system has maximal rank, in the sense that the differentials satisfy the following independence condition:

Note that this condition is strictly stronger than needed to apply the implicit function theorem
: in particular, M is a manifold of real dimension 2n − k. We say that M is an embedded CR manifold of CR codimension k. In most applications, k = 1, in which case the manifold is said to be of hypersurface type.
Let L ⊂ T(1,0)Cn|M be the subbundle of vectors annihilating all of the defining functions F1, ..., Fk. Note that, by the usual considerations for integrable distributions on hypersurfaces, L is involutive. Moreover, the independence condition implies that L is a bundle of constant rank n − k.
Henceforth, suppose that k = 1 (so that the CR manifold is of hypersurface type), unless otherwise noted.
, is the Hermitian 2-form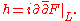
This determines a metric on L. M is said to be strictly pseudoconvex if h is positive definite (or pseudoconvex in case h is positive semidefinite). Many of the analytic existence and uniqueness results in the theory of CR manifolds depend on the strict pseudoconvexity of the Levi form.
This nomenclature comes from the study of pseudoconvex domains: M is the boundary of a (strictly) pseudoconvex domain in Cn if and only if it is (strictly) pseudoconvex as a CR manifold. (See plurisubharmonic function
s and Stein manifold
.)
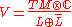
given by
h defines a sesquilinear form on L since it does not depend on how v and w are extended to sections of L, by the integrability condition. This form extends to a hermitian form on the bundle by the same expression. The extended form is also sometimes referred to as the Levi form.
by the same expression. The extended form is also sometimes referred to as the Levi form.
The Levi form can alternatively be characterized in terms of duality. Consider the line subbundle of the complex cotangent bundle
annihilating V
For each local section α∈Γ(H0M), let
The form hα is a complex-valued hermitian form associated to α.
Generalizations of the Levi form exist when the manifold is not of hypersurface type, in which case the form no longer assumes values in a line bundle, but rather in a vector bundle. One may then speak, not of a Levi form, but of a collection of Levi forms for the structure.
 sphere as a submanifold of
sphere as a submanifold of 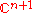 . The bundle
. The bundle  described above is given by
described above is given by
where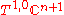 is the bundle of holomorphic vectors. The real form of this is given by
is the bundle of holomorphic vectors. The real form of this is given by  , the bundle given at a point
, the bundle given at a point 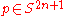 concretely in terms of the complex structure,
concretely in terms of the complex structure, 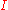 , on
, on 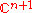 by
by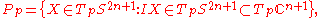
and the almost complex structure on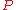 is just the restriction of
is just the restriction of 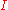 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a CR manifold is a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
together with a geometric structure modeled on that of a real hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
in a complex vector space
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, or more generally modeled on an edge of a wedge
Edge-of-the-wedge theorem
In mathematics, Bogoliubov's edge-of-the-wedge theorem implies that holomorphic functions on two "wedges" with an "edge" in common are analytic continuations of each other provided they both give the same continuous function on the edge. It is used in quantum field theory to construct the...
.
Formally, a CR manifold is a differentiable manifold M together with a preferred complex distribution L, or in other words a subbundle
Subbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
of the complexified tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
CTM = TM ⊗ C such that
-
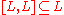 (L is formally integrable)
(L is formally integrable) -
 (L is almost Lagrangian).
(L is almost Lagrangian).
The bundle L is called a CR structure on the manifold M.
The abbreviation CR stands for Cauchy-Riemann or Complex-Real.
Introduction and motivation
The notion of a CR structure attempts to describe intrinsically the property of being a hypersurface in complex space by studying the properties of holomorphic vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s which are tangent to the hypersurface.
Suppose for instance that M is the hypersurface of C2 given by the equation
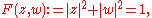
where z and w are the usual complex coordinates on C2. The holomorphic tangent bundle of C2 consists of all linear combinations of the vectors
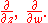
The distribution L on M consists of all combinations of these vectors which are tangent to M. In detail, the tangent vectors must annihilate the defining equation for M, so L consists of complex scalar multiples of
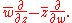
Note that L gives a CR structure on M, for [L,L] = 0 (since L is one-dimensional) and
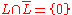 since ∂/∂z and ∂/∂w are linearly independent of their complex conjugates.
since ∂/∂z and ∂/∂w are linearly independent of their complex conjugates.More generally, suppose that M is a real hypersurface in Cn, with defining equation F(z1, ..., zn) = 0. Then the CR structure L consists of those linear combinations of the basic holomorphic vectors on Cn:

which annihilate the defining function. In this case,
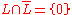 for the same reason as before. Moreover, [L,L] ⊂ L since the commutator of vector fields annihilating F is again a vector field annihilating F.
for the same reason as before. Moreover, [L,L] ⊂ L since the commutator of vector fields annihilating F is again a vector field annihilating F.Embedded and abstract CR manifolds
There is a sharp contrast between the theories of embedded CR manifolds (hypersurface and edges of wedges in complex space) and abstract CR manifolds (those given by the Lagrangian distribution L). Many of the formal geometrical features are similar. These include:- A notion of convexityConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
(supplied by the Levi form) - A differential operatorDifferential operatorIn mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
, analogous to the Dolbeault operator, and an associated cohomologyCohomologyIn mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
(the tangential Cauchy-Riemann complex).
Embedded CR manifolds possess some additional structure, though: a Neumann and Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for the Cauchy-Riemann equations.
This article first treats the geometry of embedded CR manifolds, shows how to defined these structures intrinsically, and then generalizes these to the abstract setting.
Preliminaries
Embedded CR manifolds are, first and foremost, submanifolds of Cn. Define a pair of subbundles of the complexified tangent bundle C ⊗ TC'n by:- T(1,0)Cn consists of the complex vectors annihilating the antiholomorphic functions. In the holomorphic coordinatesComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
:
-
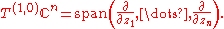
- T(0,1)Cn consists of the complex vectors annihilating the holomorphic functions. In coordinates:
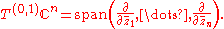
Also relevant are the characteristic annihilators from the Dolbeault complex:
- Ω(1,0)Cn = (T(0,1)Cn)⊥. In coordinates,
-
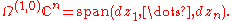
- Ω(0,1)Cn = (T(1,0)Cn)⊥. In coordinates,

The exterior products of these are denoted by the self-evident notation Ω(p,q), and the Dolbeault operator and its complex conjugate map between these spaces via


Furthermore, there is a decomposition of the usual exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
via
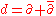 .
.Real submanifolds of complex space
Let M ⊂ Cn be a real submanifold, defined locally as the locus of a system of smooth real-valued functions- F1 = 0, F2 = 0, ..., Fk = 0.
Suppose that this system has maximal rank, in the sense that the differentials satisfy the following independence condition:

Note that this condition is strictly stronger than needed to apply the implicit function theorem
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
: in particular, M is a manifold of real dimension 2n − k. We say that M is an embedded CR manifold of CR codimension k. In most applications, k = 1, in which case the manifold is said to be of hypersurface type.
Let L ⊂ T(1,0)Cn|M be the subbundle of vectors annihilating all of the defining functions F1, ..., Fk. Note that, by the usual considerations for integrable distributions on hypersurfaces, L is involutive. Moreover, the independence condition implies that L is a bundle of constant rank n − k.
Henceforth, suppose that k = 1 (so that the CR manifold is of hypersurface type), unless otherwise noted.
The Levi form
Let M be a CR manifold of hypersurface type with single defining function F = 0. The Levi form of M, named after Eugenio Elia LeviEugenio Elia Levi
Eugenio Elia Levi was an Italian mathematician, known for his fundamental contributions in group theory, in the theory of partial differential operators and in the theory of functions of several complex variables: he was the younger brother of Beppo Levi and died in the First World War.-Research...
, is the Hermitian 2-form
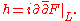
This determines a metric on L. M is said to be strictly pseudoconvex if h is positive definite (or pseudoconvex in case h is positive semidefinite). Many of the analytic existence and uniqueness results in the theory of CR manifolds depend on the strict pseudoconvexity of the Levi form.
This nomenclature comes from the study of pseudoconvex domains: M is the boundary of a (strictly) pseudoconvex domain in Cn if and only if it is (strictly) pseudoconvex as a CR manifold. (See plurisubharmonic function
Plurisubharmonic function
In mathematics, plurisubharmonic functions form an important class of functions used in complex analysis. On a Kähler manifold, plurisubharmonic functions form a subset of the subharmonic functions...
s and Stein manifold
Stein manifold
In mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.- Definition :...
.)
Abstract CR structures
An abstract CR structure on a manifold M of dimension n consists of a subbundle L of the complexified tangent bundle which is formally integrable, in the sense that [L,L] ⊂ L, which is linearly independent of its complex conjugate. The CR codimension of the CR structure is k = n - 2 dim L. In case k = 1, the CR structure is said to be of hypersurface type. Most examples of abstract CR structures are of hypersurface type, unless otherwise made explicit.The Levi form and pseudoconvexity
Suppose that M is a CR manifold of hypersurface type. The Levi form is the vector valued form, defined on L, with values in the line bundleLine bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
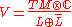
given by

h defines a sesquilinear form on L since it does not depend on how v and w are extended to sections of L, by the integrability condition. This form extends to a hermitian form on the bundle
 by the same expression. The extended form is also sometimes referred to as the Levi form.
by the same expression. The extended form is also sometimes referred to as the Levi form.The Levi form can alternatively be characterized in terms of duality. Consider the line subbundle of the complex cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
annihilating V

For each local section α∈Γ(H0M), let

The form hα is a complex-valued hermitian form associated to α.
Generalizations of the Levi form exist when the manifold is not of hypersurface type, in which case the form no longer assumes values in a line bundle, but rather in a vector bundle. One may then speak, not of a Levi form, but of a collection of Levi forms for the structure.
Examples
The canonical example of a CR manifold is the real sphere as a submanifold of
sphere as a submanifold of 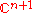 . The bundle
. The bundle  described above is given by
described above is given by
where
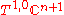 is the bundle of holomorphic vectors. The real form of this is given by
is the bundle of holomorphic vectors. The real form of this is given by  , the bundle given at a point
, the bundle given at a point 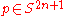 concretely in terms of the complex structure,
concretely in terms of the complex structure, 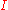 , on
, on 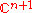 by
by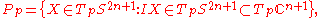
and the almost complex structure on
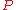 is just the restriction of
is just the restriction of 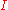 .
.

