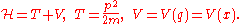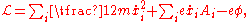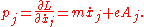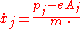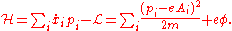Hamiltonian mechanics
Encyclopedia
Hamiltonian mechanics is a reformulation of classical mechanics
that was introduced in 1833 by Irish mathematician William Rowan Hamilton
.
It arose from Lagrangian mechanics
, a previous reformulation of classical mechanics
introduced by Joseph Louis Lagrange
in 1788, but can be formulated without recourse to Lagrangian mechanics using symplectic spaces
(see Mathematical formalism, below). The Hamiltonian method differs from the Lagrangian method in that instead of expressing second-order differential constraints on an n-dimensional coordinate space
(where n is the number of degrees of freedom of the system), it expresses first-order constraints on a 2n-dimensional phase space
.
As with Lagrangian mechanics, Hamilton's equations provide a new and equivalent way of looking at classical mechanics. Generally, these equations do not provide a more convenient way of solving a particular problem. Rather, they provide deeper insights into both the general structure of classical mechanics and its connection to quantum mechanics
as understood through Hamiltonian mechanics, as well as its connection to other areas of science.
and potential energy
in the system. There is a set of differential equation
s known as the Hamilton equations which give the time evolution of the system. Hamiltonians can be used to describe such simple systems as a bouncing ball, a pendulum or an oscillating spring in which energy changes from kinetic to potential and back again over time. Hamiltonians can also be employed to model the energy of other more complex dynamic systems such as planetary orbits in celestial mechanics
and also in quantum mechanics.
The Hamilton equations are generally written as follows:
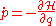
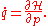
In the above equations, the dot denotes the ordinary derivative with respect to time of the functions
(called generalized momenta) and (called generalized coordinates
), taking values in some vector space, and =
= 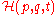 is the so-called Hamiltonian, or (scalar valued) Hamiltonian function. Thus, more explicitly, one can equivalently write
is the so-called Hamiltonian, or (scalar valued) Hamiltonian function. Thus, more explicitly, one can equivalently write
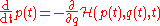
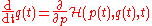
and specify the domain of values in which the parameter t (time) varies.
For a detailed derivation of these equations from Lagrangian mechanics
, see below.
The Hamiltonian represents the energy
represents the energy
of the system (provided that there are NO external forces, or additional energy added to the system),
which is the sum of kinetic
and potential energy
, traditionally denoted T and V, respectively. Here q is the x coordinate and p is the momentum, mv. Then
Note that T is a function of p alone, while V is a function of x (or q) alone.
Now the time-derivative of the momentum p equals the Newtonian force, and so here the first Hamilton equation means that the force on the particle equals the rate at which it loses potential energy with respect to changes in x, its location. (Force equals the negative gradient
of potential energy.)
The time-derivative of q here means the velocity: the second Hamilton equation here means that the particle’s velocity equals the derivative of its kinetic energy with respect to its momentum. (Because the derivative with respect to p of p2/2m equals p/m = mv/m = v.)
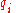 and generalized velocities
and generalized velocities 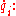
depends on time, generalized positions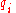 and generalized velocities
and generalized velocities 
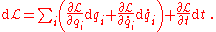
Now the generalized momenta were defined as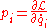 and Lagrange's equations tell us that
and Lagrange's equations tell us that
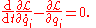
We can rearrange this to get
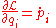
and substitute the result into the total differential of the Lagrangian
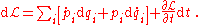
We can rewrite this as
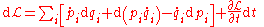
and rearrange again to get

The term on the left-hand side is just the Hamiltonian that we have defined before, so we find that

where the second equality holds because of the definition of the total differential of in terms of its partial derivatives. Associating terms from both sides of the equation above yields Hamilton's equations
in terms of its partial derivatives. Associating terms from both sides of the equation above yields Hamilton's equations
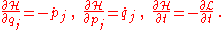
, the equations of motion
are based on generalized coordinates
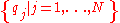
and matching generalized velocities
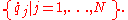
We write the Lagrangian
as

with the subscripted variables understood to represent all N variables of that type. Hamiltonian mechanics aims to replace the generalized velocity variables with generalized momentum variables, also known as conjugate momenta. By doing so, it is possible to handle certain systems, such as aspects of quantum mechanics, that would otherwise be even more complicated.
For each generalized velocity, there is one corresponding conjugate momentum, defined as:
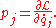
In Cartesian coordinates, the generalized momenta are precisely the physical linear momenta
. In circular polar coordinates, the generalized momentum corresponding to the angular velocity is the physical angular momentum
. For an arbitrary choice of generalized coordinates, it may not be possible to obtain an intuitive interpretation of the conjugate momenta.
One thing which is not too obvious in this coordinate dependent formulation is that different generalized coordinates are really nothing more than different coordinatizations of the same symplectic manifold
.
The Hamiltonian is the Legendre transform
of the Lagrangian
:
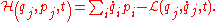
If the transformation equations defining the generalized coordinates are independent of t, and the Lagrangian is a sum of products of functions (in the generalised coordinates) which are homogeneous of order 0, 1 or 2, then it can be shown that H is equal to the total energy E = T + V.
Each side in the definition of produces a differential:
produces a differential:
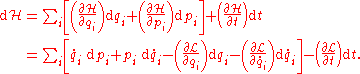
Substituting the previous definition of the conjugate momenta into this equation and matching coefficients, we obtain the equations of motion of Hamiltonian mechanics, known as the canonical equations of Hamilton:

Hamilton's equations are first-order differential equation
s, and thus easier to solve than Lagrange's equations, which are second-order. Hamilton's equations have another advantage over Lagrange's equations: if a system has a symmetry, such that a coordinate does not occur in the Hamiltonian, the corresponding momentum is conserved, and that coordinate can be ignored in the other equations of the set. Effectively, this reduces the problem from n coordinates to (n-1) coordinates. In the Lagrangian framework, of course the result that the corresponding momentum is conserved still follows immediately, but all the generalized velocities still occur in the Lagrangian - we still have to solve a system of equations in n coordinates.
The Lagrangian and Hamiltonian approaches provide the groundwork for deeper results in the theory of classical mechanics, and for formulations of quantum mechanics.
E over time
R, with the fiber
s Et, t ∈ R being the position space. The Lagrangian is thus a function on the jet bundle
J over E; taking the fiberwise Legendre transform of the Lagrangian produces a function on the dual bundle over time whose fiber at t is the cotangent space
T*Et, which comes equipped with a natural symplectic form, and this latter function is the Hamiltonian.
, but not for quantum mechanics
, since the differential equations discussed assume that one can specify the exact position and momentum of the particle simultaneously at any point in time. However, the equations can be further generalized to then be extended to apply to quantum mechanics as well as to classical mechanics, through the deformation of the Poisson algebra
over p and q to the algebra of Moyal bracket
s.
Specifically, the more general form of the Hamilton's equation reads
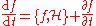
where f is some function of p and q, and H is the Hamiltonian. To find out the rules for evaluating a Poisson bracket
without resorting to differential equations, see Lie algebra
; a Poisson bracket is the name for the Lie bracket in a Poisson algebra
. These Poisson brackets can then be extended to Moyal bracket
s comporting to an inequivalent Lie algebra,
as proven by H Groenewold, and thereby describe quantum mechanical diffusion in phase space (See the uncertainty principle
and Weyl quantization
).
This more algebraic approach not only permits ultimately
extending probability distribution
s in phase space
to
Wigner quasi-probability distribution
s, but, at the mere Poisson bracket classical setting, also provides more power in helping analyze the relevant conserved quantities
in a system.
real-valued function H on a symplectic manifold
can be used to define a Hamiltonian system
. The function H is known as the Hamiltonian or the energy function. The symplectic manifold is then called the phase space
. The Hamiltonian induces a special vector field
on the symplectic manifold, known as the symplectic vector field.
The symplectic vector field, also called the Hamiltonian vector field, induces a Hamiltonian flow on the manifold. The integral curve
s of the vector field are a one-parameter family of transformations of the manifold; the parameter of the curves is commonly called the time. The time evolution is given by symplectomorphism
s. By Liouville's theorem
, each symplectomorphism preserves the volume form
on the phase space
. The collection of symplectomorphisms induced by the Hamiltonian flow is commonly called the Hamiltonian mechanics of the Hamiltonian system.
The symplectic structure induces a Poisson bracket
. The Poisson bracket gives the space of functions on the manifold the structure of a Lie algebra
.
Given a function f

If we have a probability distribution
, ρ, then (since the phase space velocity (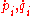 ) has zero divergence, and probability is conserved) its convective derivative can be shown to be zero and so
) has zero divergence, and probability is conserved) its convective derivative can be shown to be zero and so

This is called Liouville's theorem
. Every smooth function
G over the symplectic manifold
generates a one-parameter family of symplectomorphism
s and if { G, H } = 0, then G is conserved and the symplectomorphisms are symmetry transformations.
A Hamiltonian may have multiple conserved quantities Gi. If the symplectic manifold has dimension 2n and there are n functionally independent conserved quantities Gi which are in involution (i.e., { Gi, Gj } = 0), then the Hamiltonian is Liouville integrable. The Liouville–Arnol'd theorem says that locally, any Liouville integrable Hamiltonian can be transformed via a symplectomorphism in a new Hamiltonian with the conserved quantities Gi as coordinates; the new coordinates are called action-angle coordinates. The transformed Hamiltonian depends only on the Gi, and hence the equations of motion have the simple form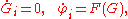
for some function F (Arnol'd et al., 1988). There is an entire field focusing on small deviations from integrable systems governed by the KAM theorem.
The integrability of Hamiltonian vector fields is an open question. In general, Hamiltonian systems are chaotic
; concepts of measure, completeness, integrability and stability are poorly defined. At this time, the study of dynamical systems is primarily qualitative, and not a quantitative science.
s, that is, Hamiltonians that can be written as
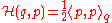
where is a smoothly varying inner product on the fibers
is a smoothly varying inner product on the fibers 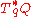 , the cotangent space
, the cotangent space
to the point q in the configuration space
, sometimes called a cometric. This Hamiltonian consists entirely of the kinetic term
.
If one considers a Riemannian manifold
or a pseudo-Riemannian manifold
, the Riemannian metric
induces a linear isomorphism between the tangent and cotangent bundles. (See Musical isomorphism
). Using this isomorphism, one can define a cometric. (In coordinates, the matrix defining the cometric is the inverse of the matrix defining the metric.) The solutions to the Hamilton–Jacobi equation
s for this Hamiltonian are then the same as the geodesic
s on the manifold. In particular, the Hamiltonian flow in this case is the same thing as the geodesic flow. The existence of such solutions, and the completeness of the set of solutions, are discussed in detail in the article on geodesic
s. See also Geodesics as Hamiltonian flows
.
of the cometric is less than the dimension of the manifold Q, one has a sub-Riemannian manifold
.
The Hamiltonian in this case is known as a sub-Riemannian Hamiltonian. Every such Hamiltonian uniquely determines the cometric, and vice-versa. This implies that every sub-Riemannian manifold
is uniquely determined by its sub-Riemannian Hamiltonian, and that the converse is true: every sub-Riemannian manifold has a unique sub-Riemannian Hamiltonian. The existence of sub-Riemannian geodesics is given by the Chow-Rashevskii theorem.
The continuous, real-valued Heisenberg group provides a simple example of a sub-Riemannian manifold. For the Heisenberg group, the Hamiltonian is given by
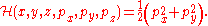
 is not involved in the Hamiltonian.
is not involved in the Hamiltonian.
of smooth function
s over a symplectic manifold
, Hamiltonian mechanics can be formulated on general commutative unital real
Poisson algebra
s. A state
is a continuous linear functional
on the Poisson algebra (equipped with some suitable topology
) such that for any element A of the algebra, A² maps to a nonnegative real number.
A further generalization is given by Nambu dynamics.
. In Cartesian coordinates (i.e. ), the Lagrangian of a non-relativistic classical particle in an electromagnetic field is (in SI Units):
), the Lagrangian of a non-relativistic classical particle in an electromagnetic field is (in SI Units):
where e is the electric charge
of the particle (not necessarily the electron charge), is the electric scalar potential
is the electric scalar potential
, and the are the components of the magnetic vector potential (these may be modified through a gauge transformation
are the components of the magnetic vector potential (these may be modified through a gauge transformation
). This is called minimal coupling
.
The generalized momenta may be derived by:
Rearranging, we may express the velocities in terms of the momenta, as:
If we substitute the definition of the momenta, and the definitions of the velocities in terms of the momenta, into the definition of the Hamiltonian given above, and then simplify and rearrange, we get:
This equation is used frequently in quantum mechanics
.

Thus the particle's canonical (total) momentum is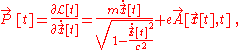
that is, the sum of the kinetic momentum and the potential momentum.
Solving for the velocity, we get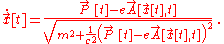
So the Hamiltonian is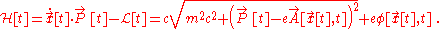
From this we get the force equation (equivalent to the Euler–Lagrange equation)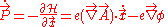
from which one can derive
An equivalent expression for the Hamiltonian as function of the relativistic (kinetic) momentum, is
is
This has the advantage that can be measured experimentally whereas
can be measured experimentally whereas  cannot. Notice that the Hamiltonian (total energy) can be viewed as the sum of the relativistic energy (kinetic+rest) ,
cannot. Notice that the Hamiltonian (total energy) can be viewed as the sum of the relativistic energy (kinetic+rest) , 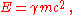 plus the potential energy
plus the potential energy
,
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
that was introduced in 1833 by Irish mathematician William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
.
It arose from Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, a previous reformulation of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
introduced by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
in 1788, but can be formulated without recourse to Lagrangian mechanics using symplectic spaces
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
(see Mathematical formalism, below). The Hamiltonian method differs from the Lagrangian method in that instead of expressing second-order differential constraints on an n-dimensional coordinate space
Coordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...
(where n is the number of degrees of freedom of the system), it expresses first-order constraints on a 2n-dimensional phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
.
As with Lagrangian mechanics, Hamilton's equations provide a new and equivalent way of looking at classical mechanics. Generally, these equations do not provide a more convenient way of solving a particular problem. Rather, they provide deeper insights into both the general structure of classical mechanics and its connection to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
as understood through Hamiltonian mechanics, as well as its connection to other areas of science.
Simplified overview of uses
The value of the Hamiltonian is the total energy of the system being described. For a closed system, it is the sum of the kineticKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
in the system. There is a set of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s known as the Hamilton equations which give the time evolution of the system. Hamiltonians can be used to describe such simple systems as a bouncing ball, a pendulum or an oscillating spring in which energy changes from kinetic to potential and back again over time. Hamiltonians can also be employed to model the energy of other more complex dynamic systems such as planetary orbits in celestial mechanics
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
and also in quantum mechanics.
The Hamilton equations are generally written as follows:
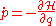
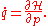
In the above equations, the dot denotes the ordinary derivative with respect to time of the functions
(called generalized momenta) and (called generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
), taking values in some vector space, and
 =
= 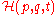 is the so-called Hamiltonian, or (scalar valued) Hamiltonian function. Thus, more explicitly, one can equivalently write
is the so-called Hamiltonian, or (scalar valued) Hamiltonian function. Thus, more explicitly, one can equivalently write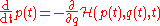
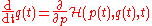
and specify the domain of values in which the parameter t (time) varies.
For a detailed derivation of these equations from Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, see below.
Basic physical interpretation
The simplest interpretation of the Hamilton equations is as follows, applying them to a one-dimensional system consisting of one particle of mass m under time-independent boundary conditions:The Hamiltonian
 represents the energy
represents the energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the system (provided that there are NO external forces, or additional energy added to the system),
which is the sum of kinetic
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, traditionally denoted T and V, respectively. Here q is the x coordinate and p is the momentum, mv. Then
Note that T is a function of p alone, while V is a function of x (or q) alone.
Now the time-derivative of the momentum p equals the Newtonian force, and so here the first Hamilton equation means that the force on the particle equals the rate at which it loses potential energy with respect to changes in x, its location. (Force equals the negative gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of potential energy.)
The time-derivative of q here means the velocity: the second Hamilton equation here means that the particle’s velocity equals the derivative of its kinetic energy with respect to its momentum. (Because the derivative with respect to p of p2/2m equals p/m = mv/m = v.)
Using Hamilton's equations
In terms of the generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
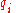 and generalized velocities
and generalized velocities 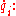
- First write out the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
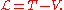 Express T and V as though you were going to use Lagrange's equation.
Express T and V as though you were going to use Lagrange's equation. - Calculate the momenta by differentiating the Lagrangian with respect to velocity:
 .
. - Express the velocities in terms of the momenta by inverting the expressions in step (2).
- Calculate the Hamiltonian using the usual definition of H as the Legendre transformationLegendre transformationIn mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
of L: . Substitute for the velocities using the results in step (3).
. Substitute for the velocities using the results in step (3). - Apply Hamilton's equations.
Deriving Hamilton's equations
We can derive Hamilton's equations by looking at how the total differential of the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
depends on time, generalized positions
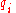 and generalized velocities
and generalized velocities 
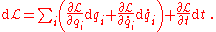
Now the generalized momenta were defined as
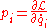 and Lagrange's equations tell us that
and Lagrange's equations tell us that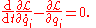
We can rearrange this to get
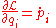
and substitute the result into the total differential of the Lagrangian
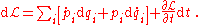
We can rewrite this as
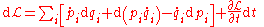
and rearrange again to get

The term on the left-hand side is just the Hamiltonian that we have defined before, so we find that

where the second equality holds because of the definition of the total differential of
 in terms of its partial derivatives. Associating terms from both sides of the equation above yields Hamilton's equations
in terms of its partial derivatives. Associating terms from both sides of the equation above yields Hamilton's equations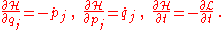
As a reformulation of Lagrangian mechanics
Starting with Lagrangian mechanicsLagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, the equations of motion
Equation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
are based on generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
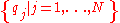
and matching generalized velocities
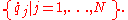
We write the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
as

with the subscripted variables understood to represent all N variables of that type. Hamiltonian mechanics aims to replace the generalized velocity variables with generalized momentum variables, also known as conjugate momenta. By doing so, it is possible to handle certain systems, such as aspects of quantum mechanics, that would otherwise be even more complicated.
For each generalized velocity, there is one corresponding conjugate momentum, defined as:
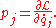
In Cartesian coordinates, the generalized momenta are precisely the physical linear momenta
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
. In circular polar coordinates, the generalized momentum corresponding to the angular velocity is the physical angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. For an arbitrary choice of generalized coordinates, it may not be possible to obtain an intuitive interpretation of the conjugate momenta.
One thing which is not too obvious in this coordinate dependent formulation is that different generalized coordinates are really nothing more than different coordinatizations of the same symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
.
The Hamiltonian is the Legendre transform
Legendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
of the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
:
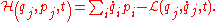
If the transformation equations defining the generalized coordinates are independent of t, and the Lagrangian is a sum of products of functions (in the generalised coordinates) which are homogeneous of order 0, 1 or 2, then it can be shown that H is equal to the total energy E = T + V.
Each side in the definition of
 produces a differential:
produces a differential: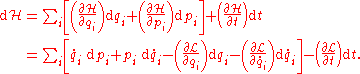
Substituting the previous definition of the conjugate momenta into this equation and matching coefficients, we obtain the equations of motion of Hamiltonian mechanics, known as the canonical equations of Hamilton:

Hamilton's equations are first-order differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, and thus easier to solve than Lagrange's equations, which are second-order. Hamilton's equations have another advantage over Lagrange's equations: if a system has a symmetry, such that a coordinate does not occur in the Hamiltonian, the corresponding momentum is conserved, and that coordinate can be ignored in the other equations of the set. Effectively, this reduces the problem from n coordinates to (n-1) coordinates. In the Lagrangian framework, of course the result that the corresponding momentum is conserved still follows immediately, but all the generalized velocities still occur in the Lagrangian - we still have to solve a system of equations in n coordinates.
The Lagrangian and Hamiltonian approaches provide the groundwork for deeper results in the theory of classical mechanics, and for formulations of quantum mechanics.
Geometry of Hamiltonian systems
A Hamiltonian system may be understood as a fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
E over time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
R, with the fiber
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
s Et, t ∈ R being the position space. The Lagrangian is thus a function on the jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
J over E; taking the fiberwise Legendre transform of the Lagrangian produces a function on the dual bundle over time whose fiber at t is the cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
T*Et, which comes equipped with a natural symplectic form, and this latter function is the Hamiltonian.
Generalization to quantum mechanics through Poisson bracket
Hamilton's equations above work well for classical mechanicsClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, but not for quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, since the differential equations discussed assume that one can specify the exact position and momentum of the particle simultaneously at any point in time. However, the equations can be further generalized to then be extended to apply to quantum mechanics as well as to classical mechanics, through the deformation of the Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
over p and q to the algebra of Moyal bracket
Moyal bracket
In physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
s.
Specifically, the more general form of the Hamilton's equation reads
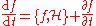
where f is some function of p and q, and H is the Hamiltonian. To find out the rules for evaluating a Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
without resorting to differential equations, see Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
; a Poisson bracket is the name for the Lie bracket in a Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
. These Poisson brackets can then be extended to Moyal bracket
Moyal bracket
In physics, the Moyal bracket is the suitably normalized antisymmetrization of the phase-space star product.The Moyal Bracket was developed in about 1940 by José Enrique Moyal, but Moyal only succeeded in publishing his work in 1949 after a lengthy dispute with Dirac...
s comporting to an inequivalent Lie algebra,
as proven by H Groenewold, and thereby describe quantum mechanical diffusion in phase space (See the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
and Weyl quantization
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
).
This more algebraic approach not only permits ultimately
extending probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
to
Wigner quasi-probability distribution
Wigner quasi-probability distribution
The Wigner quasi-probability distribution is a quasi-probability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics...
s, but, at the mere Poisson bracket classical setting, also provides more power in helping analyze the relevant conserved quantities
Conserved quantity
In mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...
in a system.
Mathematical formalism
Any smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
real-valued function H on a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
can be used to define a Hamiltonian system
Hamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
. The function H is known as the Hamiltonian or the energy function. The symplectic manifold is then called the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. The Hamiltonian induces a special vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on the symplectic manifold, known as the symplectic vector field.
The symplectic vector field, also called the Hamiltonian vector field, induces a Hamiltonian flow on the manifold. The integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s of the vector field are a one-parameter family of transformations of the manifold; the parameter of the curves is commonly called the time. The time evolution is given by symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
s. By Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
, each symplectomorphism preserves the volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
on the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. The collection of symplectomorphisms induced by the Hamiltonian flow is commonly called the Hamiltonian mechanics of the Hamiltonian system.
The symplectic structure induces a Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
. The Poisson bracket gives the space of functions on the manifold the structure of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
.
Given a function f

If we have a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, ρ, then (since the phase space velocity (
 ) has zero divergence, and probability is conserved) its convective derivative can be shown to be zero and so
) has zero divergence, and probability is conserved) its convective derivative can be shown to be zero and so
This is called Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
. Every smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
G over the symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
generates a one-parameter family of symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
s and if { G, H } = 0, then G is conserved and the symplectomorphisms are symmetry transformations.
A Hamiltonian may have multiple conserved quantities Gi. If the symplectic manifold has dimension 2n and there are n functionally independent conserved quantities Gi which are in involution (i.e., { Gi, Gj } = 0), then the Hamiltonian is Liouville integrable. The Liouville–Arnol'd theorem says that locally, any Liouville integrable Hamiltonian can be transformed via a symplectomorphism in a new Hamiltonian with the conserved quantities Gi as coordinates; the new coordinates are called action-angle coordinates. The transformed Hamiltonian depends only on the Gi, and hence the equations of motion have the simple form
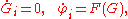
for some function F (Arnol'd et al., 1988). There is an entire field focusing on small deviations from integrable systems governed by the KAM theorem.
The integrability of Hamiltonian vector fields is an open question. In general, Hamiltonian systems are chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
; concepts of measure, completeness, integrability and stability are poorly defined. At this time, the study of dynamical systems is primarily qualitative, and not a quantitative science.
Riemannian manifolds
An important special case consists of those Hamiltonians that are quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s, that is, Hamiltonians that can be written as
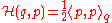
where
 is a smoothly varying inner product on the fibers
is a smoothly varying inner product on the fibers 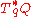 , the cotangent space
, the cotangent spaceCotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
to the point q in the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
, sometimes called a cometric. This Hamiltonian consists entirely of the kinetic term
Kinetic term
In physics, a kinetic term is the part of the Lagrangian that is bilinear in the fields , and usually contains two derivatives with respect to time ; in the case of fermions, the kinetic term usually has one derivative only...
.
If one considers a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
or a pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, the Riemannian metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
induces a linear isomorphism between the tangent and cotangent bundles. (See Musical isomorphism
Musical isomorphism
In mathematics, the musical isomorphism is an isomorphism between the tangent bundle TM and the cotangent bundle T*M of a Riemannian manifold given by its metric. There are similar isomorphisms on symplectic manifolds....
). Using this isomorphism, one can define a cometric. (In coordinates, the matrix defining the cometric is the inverse of the matrix defining the metric.) The solutions to the Hamilton–Jacobi equation
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s for this Hamiltonian are then the same as the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s on the manifold. In particular, the Hamiltonian flow in this case is the same thing as the geodesic flow. The existence of such solutions, and the completeness of the set of solutions, are discussed in detail in the article on geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. See also Geodesics as Hamiltonian flows
Geodesics as Hamiltonian flows
In mathematics, the geodesic equations are second-order non-linear differential equations, and are commonly presented in the form of Euler–Lagrange equations of motion. However, they can also be presented as a set of coupled first-order equations, in the form of Hamilton's equations...
.
Sub-Riemannian manifolds
When the cometric is degenerate, then it is not invertible. In this case, one does not have a Riemannian manifold, as one does not have a metric. However, the Hamiltonian still exists. In the case where the cometric is degenerate at every point q of the configuration space manifold Q, so that the rankRank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of the cometric is less than the dimension of the manifold Q, one has a sub-Riemannian manifold
Sub-Riemannian manifold
In mathematics, a sub-Riemannian manifold is a certain type of generalization of a Riemannian manifold. Roughly speaking, to measure distances in a sub-Riemannian manifold, you are allowed to go only along curves tangent to so-called horizontal subspaces....
.
The Hamiltonian in this case is known as a sub-Riemannian Hamiltonian. Every such Hamiltonian uniquely determines the cometric, and vice-versa. This implies that every sub-Riemannian manifold
Sub-Riemannian manifold
In mathematics, a sub-Riemannian manifold is a certain type of generalization of a Riemannian manifold. Roughly speaking, to measure distances in a sub-Riemannian manifold, you are allowed to go only along curves tangent to so-called horizontal subspaces....
is uniquely determined by its sub-Riemannian Hamiltonian, and that the converse is true: every sub-Riemannian manifold has a unique sub-Riemannian Hamiltonian. The existence of sub-Riemannian geodesics is given by the Chow-Rashevskii theorem.
The continuous, real-valued Heisenberg group provides a simple example of a sub-Riemannian manifold. For the Heisenberg group, the Hamiltonian is given by
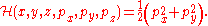
 is not involved in the Hamiltonian.
is not involved in the Hamiltonian.Poisson algebras
Hamiltonian systems can be generalized in various ways. Instead of simply looking at the algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s over a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
, Hamiltonian mechanics can be formulated on general commutative unital real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
s. A state
State (functional analysis)
In functional analysis, a state on a C*-algebra is a positive linear functional of norm 1. The set of states of a C*-algebra A, sometimes denoted by S, is always a convex set. The extremal points of S are called pure states...
is a continuous linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on the Poisson algebra (equipped with some suitable topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
) such that for any element A of the algebra, A² maps to a nonnegative real number.
A further generalization is given by Nambu dynamics.
Charged particle in an electromagnetic field
A good illustration of Hamiltonian mechanics is given by the Hamiltonian of a charged particle in an electromagnetic fieldElectromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. In Cartesian coordinates (i.e.
 ), the Lagrangian of a non-relativistic classical particle in an electromagnetic field is (in SI Units):
), the Lagrangian of a non-relativistic classical particle in an electromagnetic field is (in SI Units):where e is the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of the particle (not necessarily the electron charge),
 is the electric scalar potential
is the electric scalar potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
, and the
 are the components of the magnetic vector potential (these may be modified through a gauge transformation
are the components of the magnetic vector potential (these may be modified through a gauge transformationGauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
). This is called minimal coupling
Minimal coupling
In physics, minimal coupling refers to a coupling between fields which involves only the charge distribution and not higher multipole moments of the charge distribution...
.
The generalized momenta may be derived by:
Rearranging, we may express the velocities in terms of the momenta, as:
If we substitute the definition of the momenta, and the definitions of the velocities in terms of the momenta, into the definition of the Hamiltonian given above, and then simplify and rearrange, we get:
This equation is used frequently in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Relativistic charged particle in an electromagnetic field
The Lagrangian for a relativistic charged particle is given by:
Thus the particle's canonical (total) momentum is
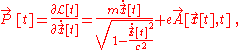
that is, the sum of the kinetic momentum and the potential momentum.
Solving for the velocity, we get
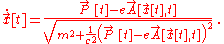
So the Hamiltonian is
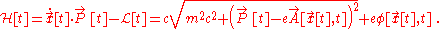
From this we get the force equation (equivalent to the Euler–Lagrange equation)
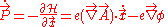
from which one can derive

An equivalent expression for the Hamiltonian as function of the relativistic (kinetic) momentum,
 is
is
This has the advantage that
 can be measured experimentally whereas
can be measured experimentally whereas  cannot. Notice that the Hamiltonian (total energy) can be viewed as the sum of the relativistic energy (kinetic+rest) ,
cannot. Notice that the Hamiltonian (total energy) can be viewed as the sum of the relativistic energy (kinetic+rest) , 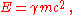 plus the potential energy
plus the potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
,

See also
- Canonical transformationCanonical transformationIn Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
- Classical field theoryClassical field theoryA classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
- Classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
- Dynamical systems theoryDynamical systems theoryDynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
- Hamilton–Jacobi equationHamilton–Jacobi equationIn mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
- Hamiltonian (quantum mechanics)Hamiltonian (quantum mechanics)In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
- Quantum Hamilton's equationsMethod of quantum characteristicsIn quantum mechanics, quantum characteristics are phase-space trajectories that arise in the deformation quantization through the Weyl-Wigner transform of Heisenberg operators of canonical coordinates and momenta...
- Quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- Hamiltonian opticsHamiltonian opticsLagrangian optics and Hamiltonian optics are two formulations of geometrical optics which share much of the mathematical formalism with Lagrangian mechanics and Hamiltonian mechanics.-Hamilton's principle:...