
Heat kernel
Encyclopedia
In the mathematical
study of heat conduction
and diffusion
, a heat kernel is the fundamental solution
to the heat equation
on a particular domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum
of the Laplace operator
, and is thus of some auxiliary importance throughout mathematical physics
. The heat kernel represents the evolution of temperature
in a region whose boundary is held fixed at a particular temperature (typically zero), such that an initial unit of heat energy is placed at a point at time t = 0.
The most well-known heat kernel is the heat kernel of d-dimensional Euclidean space
Rd, which has the form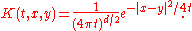
This solves the heat equation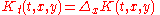
for all t > 0 and x,y ∈ Rd, with the initial condition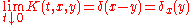
where δ is a Dirac delta distribution and the limit is taken in the sense of distributions
. To wit, for every smooth function φ of compact support,
On a more general domain Ω in Rd, such an explicit formula is not generally possible. The next simplest cases of a disc or square involve, respectively, Bessel functions and Jacobi theta functions. Nevertheless, the heat kernel (for, say, the Dirichlet problem
) still exists and is smooth
for t > 0 on arbitrary domains and indeed on any Riemannian manifold
with boundary, provided the boundary is sufficiently regular. More precisely, in these more general domains, the heat kernel for the Dirichlet problem is the solution of the initial boundary value problem
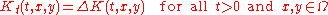
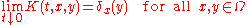

It is not difficult to derive a formal expression for the heat kernel on an arbitrary domain. Consider the Dirichlet problem in a connected domain (or manifold with boundary) U. Let λn be the eigenvalues for the Dirichlet problem of the Laplacian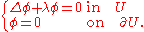
Let φn denote the associated eigenfunction
s, normalized to be orthonormal in L2(U)
. The inverse Dirichlet Laplacian Δ−1 is a compact
and selfadjoint operator, and so the spectral theorem
implies that the eigenvalues satisfy
The heat kernel has the following expression:
Formally differentiating the series under the sign of the summation shows that this should satisfy the heat equation. However, convergence and regularity of the series are quite delicate.
The heat kernel is also sometimes identified with the associated integral transform, defined for compactly supported smooth φ by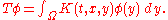
The spectral mapping theorem gives a representation of T in the form
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
study of heat conduction
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
and diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
, a heat kernel is the fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
to the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
on a particular domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
of the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, and is thus of some auxiliary importance throughout mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
. The heat kernel represents the evolution of temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
in a region whose boundary is held fixed at a particular temperature (typically zero), such that an initial unit of heat energy is placed at a point at time t = 0.
The most well-known heat kernel is the heat kernel of d-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rd, which has the form
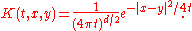
This solves the heat equation
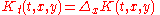
for all t > 0 and x,y ∈ Rd, with the initial condition
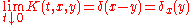
where δ is a Dirac delta distribution and the limit is taken in the sense of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
. To wit, for every smooth function φ of compact support,

On a more general domain Ω in Rd, such an explicit formula is not generally possible. The next simplest cases of a disc or square involve, respectively, Bessel functions and Jacobi theta functions. Nevertheless, the heat kernel (for, say, the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
) still exists and is smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
for t > 0 on arbitrary domains and indeed on any Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with boundary, provided the boundary is sufficiently regular. More precisely, in these more general domains, the heat kernel for the Dirichlet problem is the solution of the initial boundary value problem
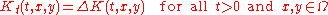
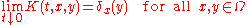

It is not difficult to derive a formal expression for the heat kernel on an arbitrary domain. Consider the Dirichlet problem in a connected domain (or manifold with boundary) U. Let λn be the eigenvalues for the Dirichlet problem of the Laplacian
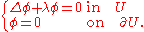
Let φn denote the associated eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s, normalized to be orthonormal in L2(U)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. The inverse Dirichlet Laplacian Δ−1 is a compact
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
and selfadjoint operator, and so the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
implies that the eigenvalues satisfy

The heat kernel has the following expression:
Formally differentiating the series under the sign of the summation shows that this should satisfy the heat equation. However, convergence and regularity of the series are quite delicate.
The heat kernel is also sometimes identified with the associated integral transform, defined for compactly supported smooth φ by
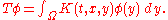
The spectral mapping theorem gives a representation of T in the form


