Knot theory - AbsoluteAstronomy.com

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, knot theory is the study of mathematical knot

Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...

s. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

of a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

in 3-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, R³. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R³ upon itself (known as an ambient isotopy

Ambient isotopy

In the mathematical subject of topology, an ambient isotopy, also called an h-isotopy, is a kind of continuous distortion of an "ambient space", a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the...

); these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.

Knots can be described in various ways. Given a method of description, however, there may be more than one description that represents the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram. Any given knot can be drawn in many different ways using a knot diagram. Therefore, a fundamental problem in knot theory is determining when two descriptions represent the same knot.

A complete algorithmic solution to this problem exists, which has unknown complexity

Computational Complexity

Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...

. In practice, knots are often distinguished by using a knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...

, a "quantity" which is the same when computed from different descriptions of a knot. Important invariants include knot polynomials, knot group

Knot group

In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....

s, and hyperbolic invariants.

The original motivation for the founders of knot theory was to create a table of knots and link

Link (knot theory)

In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...

s, which are knots of several components entangled with each other. Over six billion knots and links have been tabulated since the beginnings of knot theory in the 19th century.

To gain further insight, mathematicians have generalized the knot concept in several ways. Knots can be considered in other three-dimensional spaces

3-manifold

In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...

and objects other than circles can be used; see knot (mathematics)
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...

. Higher dimensional knots are n-dimensional spheres in m-dimensional Euclidean space.

The generalized Poincaré conjecture

Generalized Poincaré conjecture

In the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...

states that Every simply connected, closed n-manifold is homeomorphic to the n-sphere. Every n-dimensional knot can therefore be stretched into a trivial n-sphere. N-dimensional knots are generally not decomposable into 2-dimensional knots, though they can be projected to superpositions of lower-dimensional knots.

History

Archaeologists have discovered that knot tying dates back to prehistoric times. Besides their uses such as recording information and tying

Knot tying

thumb|right|[[The Ashley Book of Knots]] is considered the definitive work on the topicKnot tying consists of the techniques and skills employed in tying a knot in rope, nylon webbing, or other articles. The proper tying of a knot can be the difference between an attractive knot and a messy one,...

objects together, knots have interested humans for their aesthetics and spiritual symbolism. Knots appear in various forms of Chinese artwork dating from several centuries BC (see Chinese knotting). The endless knot

Endless knot

The endless knot or eternal knot is a symbolic knot and one of the Eight Auspicious Symbols. It is an important cultural marker in places significantly influenced by Tibetan Buddhism such as Tibet, Mongolia, Tuva, Kalmykia, and Buryatia...

appears in Tibetan Buddhism

Tibetan Buddhism

Tibetan Buddhism is the body of Buddhist religious doctrine and institutions characteristic of Tibet and certain regions of the Himalayas, including northern Nepal, Bhutan, and India . It is the state religion of Bhutan...

, while the Borromean rings

Borromean rings

In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...

have made repeated appearances in different cultures, often representing strength in unity. The Celtic

Celtic Christianity

Celtic Christianity or Insular Christianity refers broadly to certain features of Christianity that were common, or held to be common, across the Celtic-speaking world during the Early Middle Ages...

monks who created the Book of Kells

Book of Kells

The Book of Kells is an illuminated manuscript Gospel book in Latin, containing the four Gospels of the New Testament together with various prefatory texts and tables. It was created by Celtic monks ca. 800 or slightly earlier...

lavished entire pages with intricate Celtic knot

Celtic knot

Celtic knots are a variety of knots and stylized graphical representations of knots used for decoration, used extensively in the Celtic style of Insular art. These knots are most known for their adaptation for use in the ornamentation of Christian monuments and manuscripts, such as the 8th-century...

work.

Mathematical studies of knots began in the 19th century with Gauss

Gauss

Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...

, who defined the linking integral . In the 1860s, Lord Kelvin's theory that atoms were knots in the aether

Luminiferous aether

In the late 19th century, luminiferous aether or ether, meaning light-bearing aether, was the term used to describe a medium for the propagation of light....

led to Peter Guthrie Tait

Peter Guthrie Tait

Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...

's creation of the first knot tables. Tabulation motivated the early knot theorists, but knot theory eventually became part of the emerging subject of topology

Topology

.

These topologists in the early part of the 20th century—Max Dehn

Max Dehn

Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...

, J. W. Alexander

James Waddell Alexander II

James Waddell Alexander II was a mathematician and topologist of the pre-World War II era and part of an influential Princeton topology elite, which included Oswald Veblen, Solomon Lefschetz, and others...

, and others—studied knots from the point of view of the knot group

Knot group

In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....

and invariants from homology

Homology (mathematics)

In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...

theory such as the Alexander polynomial

Alexander polynomial

In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...

. This would be the main approach to knot theory until a series of breakthroughs transformed the subject.

In the late 1970s, William Thurston

William Thurston

William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...

introduced hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

into the study of knots with the hyperbolization theorem

Geometrization conjecture

Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...

. Many knots were shown to be hyperbolic knots, enabling the use of geometry in defining new, powerful knot invariant

Knot invariant

In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...

s. The discovery of the Jones polynomial by Vaughan Jones

Vaughan Jones

Sir Vaughan Frederick Randal Jones, KNZM, FRS, FRSNZ is a New Zealand mathematician, known for his work on von Neumann algebras, knot polynomials and conformal field theory. He was awarded a Fields Medal in 1990, and famously wore a New Zealand rugby jersey when he accepted the prize...

in 1984 , and subsequent contributions from Edward Witten

Edward Witten

Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....

, Maxim Kontsevich

Maxim Kontsevich

Maxim Lvovich Kontsevich is a Russian mathematician. He is a professor at the Institut des Hautes Études Scientifiques and a distinguished professor at the University of Miami...

, and others, revealed deep connections between knot theory and mathematical methods in statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

and quantum field theory

Quantum field theory

Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...

. A plethora of knot invariants have been invented since then, utilizing sophisticated tools such as quantum group

Quantum group

In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...

s and Floer homology

Floer homology

Floer homology is a mathematical tool used in the study of symplectic geometry and low-dimensional topology. First introduced by Andreas Floer in his proof of the Arnold conjecture in symplectic geometry, Floer homology is a novel homology theory arising as an infinite dimensional analog of finite...

.

In the last several decades of the 20th century, scientists became interested in studying physical knots

Physical knot theory

Physical knot theory is the study of mathematical models of knotting phenomena, often motivated by physical considerations from biology, chemistry, and physics. Traditional knot theory models a knot as a simple closed loop in three dimensional space. Such a knot has no thickness or physical...

in order to understand knotting phenomena in DNA and other polymers. Knot theory can be used to determine if a molecule is chiral

Chirality (chemistry)

A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom....

(has a "handedness") or not . Tangles, strings with both ends fixed in place, have been effectively used in studying the action of topoisomerase

Topoisomerase

Topoisomerases are enzymes that regulate the overwinding or underwinding of DNA. The winding problem of DNA arises due to the intertwined nature of its double helical structure. For example, during DNA replication, DNA becomes overwound ahead of a replication fork...

on DNA . Knot theory may be crucial in the construction of quantum computers, through the model of topological quantum computation .

Knot equivalence

A knot is created by beginning with a one-dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

al line segment, wrapping it around itself arbitrarily, and then fusing its two free ends together to form a closed loop . When topologists consider knots and other entanglements such as links

Link (knot theory)

and braid

Braid theory

In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a...

s, they consider the space surrounding the knot as a viscous fluid. If the knot can be pushed about smoothly in the fluid, without intersecting itself, to coincide with another knot, the two knots are considered equivalent. The idea of knot equivalence is to give a precise definition of when two knots should be considered the same even when positioned quite differently in space. A formal mathematical definition is that two knots are equivalent if one can be transformed into the other via a type of deformation of R³ upon itself, known as an ambient isotopy

Ambient isotopy

.

The basic problem of knot theory, the recognition problem, is determining the equivalence of two knots. Algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

s exist to solve this problem, with the first given by Wolfgang Haken

Wolfgang Haken

Wolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...

in the late 1960s . Nonetheless, these algorithms can be extremely time-consuming, and a major issue in the theory is to understand how hard this problem really is . The special case of recognizing the unknot

Unknot

The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...

, called the unknotting problem

Unknotting problem

In mathematics, the unknotting problem is the problem of algorithmically recognizing the unknot, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms...

, is of particular interest .

Knot diagrams

A useful way to visualise and manipulate knots is to project the knot onto a plane—think of the knot casting a shadow on the wall. A small change in the direction of projection will ensure that it is one-to-one

Injective function

In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...

except at the double points, called crossings, where the "shadow" of the knot crosses itself once transversely . At each crossing, to be able to recreate the original knot, the over-strand must be distinguished from the under-strand. This is often done by creating a break in the strand going underneath. The resulting diagram is an immersed plane curve with the additional data of which strand is over and which is under at each crossing. Analogously, knotted surfaces in 4-space can be related to immersed surfaces in 3-space.

Reidemeister moves

In 1927, working with this diagrammatic form of knots, J.W. Alexander and G. B. Briggs, and independently Kurt Reidemeister

Kurt Reidemeister

Kurt Werner Friedrich Reidemeister was a mathematician born in Braunschweig , Germany.He received his doctorate in 1921 with a thesis in algebraic number theory at the University of Hamburg under the supervision of Erich Hecke. In 1923 he was appointed assistant professor at the University of Vienna...

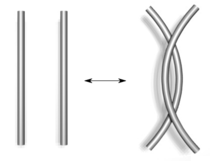
, demonstrated that two knot diagrams belonging to the same knot can be related by a sequence of three kinds of moves on the diagram, shown below. These operations, now called the Reidemeister moves, are:

Twist and untwist in either direction.

Move one strand completely over another.

Move a strand completely over or under a crossing.

**Reidemeister moves**

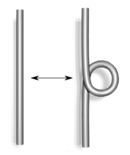Type I	Type II

Type III

The proof that diagrams of equivalent knots are connected by Reidemeister moves relies on an analysis of what happens under the planar projection of the movement taking one knot to another. The movement can be arranged so that almost all of the time the projection will be a knot diagram, except at finitely many times when an "event" or "catastrophe" occurs, such as when more than two strands cross at a point or multiple strands become tangent at a point. A close inspection will show that complicated events can be eliminated, leaving only the simplest events: (1) a "kink" forming or being straightened out; (2) two strands becoming tangent at a point and passing through; and (3) three strands crossing at a point. These are precisely the Reidemeister moves .

Knot invariants

A knot invariant is a "quantity" that is the same for equivalent knots . For example, if the invariant is computed from a knot diagram, it should give the same value for two knot diagrams representing equivalent knots. An invariant may take the same value on two different knots, so by itself may be incapable of distinguishing all knots. An elementary invariant is tricolorability

Tricolorability

In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different knots...

.

"Classical" knot invariants include the knot group

Knot group

In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....

, which is the fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

of the knot complement

Knot complement

In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...

, and the Alexander polynomial

Alexander polynomial

, which can be computed from the Alexander invariant, a module constructed from the infinite cyclic cover of the knot complement . In the late 20th century, invariants such as "quantum" knot polynomials, Vassiliev invariants and hyperbolic invariants were discovered. These aforementioned invariants are only the tip of the iceberg of modern knot theory.

Knot polynomials

A knot polynomial is a knot invariant

Knot invariant

that is a polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

. Well-known examples include the Jones and Alexander polynomial

Alexander polynomial

s. A variant of the Alexander polynomial, the Alexander–Conway polynomial, is a polynomial in the variable z with integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

coefficients .

The Alexander–Conway polynomial is actually defined in terms of links

Link (knot theory)

, which consist of one or more knots entangled with each other. The concepts explained above for knots, e.g. diagrams and Reidemeister moves, also hold for links.

Consider an oriented link diagram, i.e. one in which every component of the link has a preferred direction indicated by an arrow. For a given crossing of the diagram, let

be the oriented link diagrams resulting from changing the diagram as indicated in the figure:

Note that the original diagram might be either

, depending on the chosen crossing's configuration. Then the Alexander–Conway polynomial, C(z), is recursively defined according to the rules:

C(O) = 1 (where O is any diagram of the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...

)

The second rule is what is often referred to as a skein relation

Skein relation

A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial which is an invariant of the knot. If two diagrams have different polynomials, they represent different knots. The reverse may not...

. To check that these rules give an invariant of an oriented link, one should determine that the polynomial does not change under the three Reidemeister moves. Many important knot polynomials can be defined in this way.

The following is an example of a typical computation using a skein relation. It computes the Alexander–Conway polynomial of the trefoil knot

Trefoil knot

In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...

. The yellow patches indicate where the relation is applied.

) = C(

) + z C(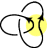

)

gives the unknot and the Hopf link

Hopf link

thumb|right|[[Skein relation]] for the Hopf link.In mathematical knot theory, the Hopf link, named after Heinz Hopf, is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly once...

. Applying the relation to the Hopf link where indicated,

) = C(

) + z C(

)

gives a link deformable to one with 0 crossings (it is actually the unlink

Unlink

In the mathematical field of knot theory, the unlink is a link that is equivalent to finitely many disjoint circles in the plane.- Properties :...

of two components) and an unknot. The unlink takes a bit of sneakiness:

) = C(

) + z C(

)

which implies that C(unlink of two components) = 0, since the first two polynomials are of the unknot and thus equal.

Putting all this together will show:

C(trefoil) = 1 + z (0 + z) = 1 + z².

Since the Alexander–Conway polynomial is a knot invariant, this shows that the trefoil is not equivalent to the unknot. So the trefoil really is "knotted".
Actually, there are two trefoil knots, called the right and left-handed trefoils, which are mirror images of each other (take a diagram of the trefoil given above and change each crossing to the other way to get the mirror image). These are not equivalent to each other, meaning that they are not amphicheiral! This was shown by Max Dehn

Max Dehn

Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...

, before the invention of knot polynomials, using group theoretical methods . But the Alexander–Conway polynomial of each kind of trefoil will be the same, as can be seen by going through the computation above with the mirror image. The Jones polynomial can in fact distinguish between the left and right-handed trefoil knots .

Hyperbolic invariants

William Thurston

proved many knots are hyperbolic knots, meaning that the knot complement

Knot complement

, i.e. the set of points of 3-space not on the knot, admits a geometric structure, in particular that of hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

. The hyperbolic structure depends only on the knot so any quantity computed from the hyperbolic structure is then a knot invariant .
Geometry lets us visualize what the inside of a knot or link complement looks like by imagining light rays as traveling along the geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s of the geometry. An example is provided by the picture of the complement of the Borromean rings

Borromean rings

. The inhabitant of this link complement is viewing the space from near the red component. The balls in the picture are views of horoball

Horoball

In hyperbolic geometry, a horoball is an object in hyperbolic n-space: the limit of a sequence of increasing balls sharing a tangent hyperplane and its point of tangency. Its boundary is called a horosphere. For n = 2 a horosphere is called a horocycle.This terminology is due to William...

neighborhoods of the link. By thickening the link in a standard way, the horoball neighborhoods of the link components are obtained. Even though the boundary of a neighborhood is a torus, when viewed from inside the link complement, it looks like a sphere. Each link component shows up as infinitely many spheres (of one color) as there are infinitely many light rays from the observer to the link component. The fundamental parallelogram (which is indicated in the picture), tiles both vertically and horizontally and shows how to extend the pattern of spheres infinitely.

This pattern, the horoball pattern, is itself a useful invariant. Other hyperbolic invariants include the shape of the fundamental paralleogram, length of shortest geodesic, and volume. Modern knot and link tabulation efforts have utilized these invariants effectively. Fast computers and clever methods of obtaining these invariants make calculating these invariants, in practice, a simple task .

Higher dimensions

In four dimensions, any non-intersecting closed loop of one-dimensional string is equivalent to an unknot. This necessary deformation can be achieved in two steps. The first step is to "push" the loop into a three-dimensional subspace, which is always possible, though technical to explain. The second step is changing crossings. Suppose one strand is behind another as seen from a chosen point. Lift it into the fourth dimension, so there is no obstacle (the front strand having no component there); then slide it forward, and drop it back, now in front. An analogy for the plane would be lifting a string up off the surface.

Since a knot can be considered topologically a 1-dimensional sphere, the next generalization is to consider a two dimensional sphere embedded in a four dimensional ball. Such an embedding is unknotted if there is a homeomorphism of the 4-sphere onto itself taking the 2-sphere to a standard "round" 2-sphere. Suspended knots and spun knots are two typical families of such 2-sphere knots.

The mathematical technique called "general position" implies that for a given n-sphere in the m-sphere, if m is large enough (depending on n), the sphere should be unknotted. In general, piecewise-linear

Piecewise linear manifold

In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...

n-spheres form knots only in (n+2)-space , although this is no longer a requirement for smoothly knotted spheres. In fact, there are smoothly knotted 4k-1-spheres in 6k-space, e.g. there is a smoothly knotted 3-sphere in the 6-sphere . Thus the codimension of a smooth knot can be arbitrarily large when not fixing the dimension of the knotted sphere; however, any smooth k-sphere in an n-sphere with 2n-3k-3 > 0 is unknotted. The notion of a knot has further generalisations in mathematics, see: knot (mathematics)

Knot (mathematics)

, isotopy classification of embeddings.

Adding knots

Two knots can be added by cutting both knots and joining the pairs of ends. The operation is called the knot sum, or sometimes the connected sum or composition of two knots. This can be formally defined as follows : consider a planar projection of each knot and suppose these projections are disjoint. Find a rectangle in the plane where one pair of opposite sides are arcs along each knot while the rest of the rectangle is disjoint from the knots. Form a new knot by deleting the first pair of opposite sides and adjoining the other pair of opposite sides. The resulting knot is a sum of the original knots. Depending on how this is done, two different knots (but no more) may result. This ambiguity in the sum can be eliminated regarding the knots as oriented, i.e. having a preferred direction of travel along the knot, and requiring the arcs of the knots in the sum are oriented consistently with the oriented boundary of the rectangle.

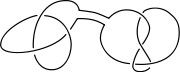
The knot sum of oriented knots is commutative and associative. A knot is prime

Prime knot

In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...

if it is non-trivial and cannot be written as the knot sum of two non-trivial knots. A knot that can be written as such a sum is composite. There is a prime decomposition for knots, analogous to prime

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

and composite numbers . For oriented knots, this decomposition is also unique. Higher dimensional knots can also be added but there are some differences. While you cannot form the unknot in three dimensions by adding two non-trivial knots, you can in higher dimensions, at least when one considers smooth knots in codimension at least 3.

Tabulating knots

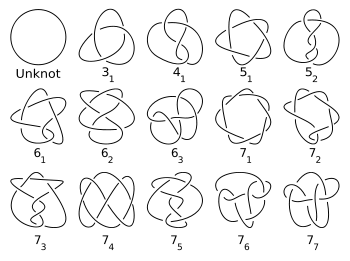
Traditionally, knots have been catalogued in terms of crossing number

Crossing number (knot theory)

In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....

. Knot tables generally include only prime knots and only one entry for a knot and its mirror image (even if they are different) . The number of nontrivial knots of a given crossing number increases rapidly, making tabulation computationally difficult . Tabulation efforts have succeeded in enumerating over 6 billion knots and links . The sequence of the number of prime knots of a given crossing number, up to crossing number 16, is 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46972, 253293, 1388705... . While exponential upper and lower bounds for this sequence are known, it has not been proven that this sequence is strictly increasing .

The first knot tables by Tait, Little, and Kirkman used knot diagrams, although Tait also used a precursor to the Dowker notation

Dowker notation

thumb|200px|A knot diagram with crossings labelled for a Dowker sequenceIn the mathematical field of knot theory, the Dowker notation, also called the Dowker–Thistlethwaite notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and...

. Different notations have been invented for knots which allow more efficient tabulation .

The early tables attempted to list all knots of at most 10 crossings, and all alternating knots of 11 crossings . The development of knot theory due to Alexander, Reidemeister, Seifert, and others eased the task of verification and tables of knots up to and including 9 crossings were published by Alexander–Briggs and Reidemeister in the late 1920s.

The first major verification of this work was done in the 1960s by John Horton Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

, who not only developed a new notation but also the Alexander–Conway polynomial . This verified the list of knots of at most 11 crossings and a new list of links up to 10 crossings. Conway found a number of omissions but only one duplication in the Tait–Little tables; however he missed the duplicates called the Perko pair

Perko pair

In the mathematical theory of knots, the Perko pair, named after Kenneth Perko, is a pair of entries in classical knot tables that actually represent the same knot. In Rolfsen's knot table, this supposed pair of distinct knots is labeled 10161 and 10162...

, which would only be noticed in 1974 by Kenneth Perko . This famous error would propagate when Dale Rolfsen added a knot table in his influential text, based on Conway's work.

In the late 1990s Hoste, Thistlethwaite, and Weeks tabulated all the knots through 16 crossings . In 2003 Rankin, Flint, and Schermann, tabulated the alternating knot

Alternating knot

In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....

s through 22 crossings .

Alexander–Briggs notation

This is the most traditional notation, due to the 1927 paper of J. W. Alexander

James Waddell Alexander II

and G. Briggs and later extended by Dale Rolfsen in his knot table. The notation simply organizes knots by their crossing number. One writes the crossing number with a subscript to denote its order amongst all knots with that crossing number. This order is arbitrary and so has no special significance.

Dowker notation

The Dowker notation, also called the Dowker–Thistlethwaite notation or code, for a knot is a finite sequence of even integers. The numbers are generated by following the knot and marking the crossings with consecutive integers. Since each crossing is visited twice, this creates a pairing of even integers with odd integers. An appropriate sign is given to indicate over and undercrossing. For example, in the figure the knot diagram has crossings labelled with the pairs (1,6) (3,−12) (5,2) (7,8) (9,−4) and (11,−10). The Dowker notation for this labelling is the sequence: 6 −12 2 8 −4 −10. A knot diagram has more than one possible Dowker notation, and there is a well-understood ambiguity when reconstructing a knot from a Dowker notation.

Conway notation

The Conway notation for knots and links, named after John Horton Conway

John Horton Conway

John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...

, is based on the theory of tangles . The advantage of this notation is that it reflects some properties of the knot or link.

The notation describes how to construct a particular link diagram of the link. Start with a basic polyhedron, a 4-valent connected planar graph with no digon

Digon

In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...

regions. Such a polyhedron is denoted first by the number of vertices then a number of asterisks which determine the polyhedron's position on a list of basic polyhedron. For example, 10** denotes the second 10-vertex polyhedron on Conway's list.

Each vertex then has an algebraic tangle substituted into it (each vertex is oriented so there is no arbitrary choice in substitution). Each such tangle has a notation consisting of numbers and + or − signs.

An example is 1*2 −3 2. The 1* denotes the only 1-vertex basic polyhedron. The 2 −3 2 is a sequence describing the continued fraction associated to a rational tangle. One inserts this tangle at the vertex of the basic polyhedron 1*.

A more complicated example is 8*3.1.2 0.1.1.1.1.1 Here again 8* refers to a basic polyhedron with 8 vertices. The periods separate the notation for each tangle.

Any link admits such a description, and it is clear this is a very compact notation even for very large crossing number. There are some further shorthands usually used. The last example is usually written 8*3:2 0, where the ones are omitted and kept the number of dots excepting the dots at the end. For an algebraic knot such as in the first example, 1* is often omitted.

Conway's pioneering paper on the subject lists up to 10-vertex basic polyhedra of which he uses to tabulate links, which have become standard for those links. For a further listing of higher vertex polyhedra, there are nonstandard choices available.

History

Knot equivalence

Knot diagrams

Reidemeister moves

Knot invariants

Knot polynomials

Hyperbolic invariants

Higher dimensions

Adding knots

Tabulating knots

Alexander–Briggs notation

Dowker notation

Conway notation

See also

Introductory textbooks

Surveys

History

Knot tables and software