
Directed graph
Encyclopedia
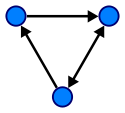
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
or digraph is a pair
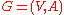 (sometimes
(sometimes 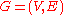 ) of:
) of:
- a set V, whose elements are called vertices or nodes,
- a set A of ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of vertices, called arcs, directed edges, or arrows (and sometimes simply edges with the corresponding set named E instead of A).
It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called edges.
Sometimes a digraph is called a simple digraph to distinguish it from a directed multigraph, in which the arcs constitute a multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
, rather than a set, of ordered pairs of vertices. Also, in a simple digraph loops are disallowed. (A loop is an arc that pairs a vertex to itself.) On the other hand, some texts allow loops, multiple arcs, or both in a digraph.
Basic terminology
An arc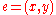 is considered to be directed from
is considered to be directed from  to
to 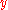 ;
; 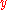 is called the head and
is called the head and  is called the tail of the arc;
is called the tail of the arc; 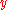 is said to be a direct successor of
is said to be a direct successor of  , and
, and  is said to be a direct predecessor of
is said to be a direct predecessor of 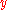 . If a path
. If a pathPath (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
made up of one or more successive arcs leads from
 to
to 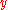 , then
, then 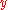 is said to be a successor of
is said to be a successor of  , and
, and  is said to be a predecessor of
is said to be a predecessor of 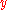 . The arc is called the arc inverted.
. The arc is called the arc inverted.A directed graph G is called symmetric if, for every arc that belongs to G, the corresponding inverted arc also belongs to G. A symmetric loopless directed graph is equivalent to an undirected graph with the pairs of inverted arcs replaced with edges; thus the number of edges is equal to the number of arcs halved.
An orientation of a simple undirected graph is obtained by assigning a direction to each edge. Any directed graph constructed this way is called an oriented graph. A distinction between a simple directed graph and an oriented graph is that if
 and
and 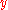 are vertices, a simple directed graph allows both
are vertices, a simple directed graph allows both 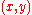 and
and 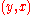 as edges, while only one is permitted in an oriented graph.
as edges, while only one is permitted in an oriented graph.A weighted digraph is a digraph with weights assigned for its arcs, similarly to the weighted graph.
A digraph with weighted edges in the context of graph theory is called a network
Network
-Mathematics:* Graph * Complex network* Structure* Flow network-Electric, electronic, biological, and biosocial: * Electrical network* Computer network* Biological network* Artificial neural network* Social network...
.
The adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of a digraph (with loops and multiple arcs) is the integer-valued matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with rows and columns corresponding to the digraph nodes, where a nondiagonal entry
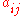 is the number of arcs from node i to node j, and the diagonal entry
is the number of arcs from node i to node j, and the diagonal entry 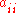 is the number of loops at node i. The adjacency matrix for a digraph is unique up to the permutations of rows and columns.
is the number of loops at node i. The adjacency matrix for a digraph is unique up to the permutations of rows and columns.Another matrix representation for a digraph is its incidence matrix
Incidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
.
See Glossary of graph theory#Direction for more definitions.
Indegree and outdegree
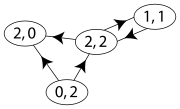
The indegree is denoted
 and the outdegree as
and the outdegree as 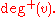 A vertex with
A vertex with 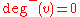 is called a source, as it is the origin of each of its incident edges. Similarly, a vertex with
is called a source, as it is the origin of each of its incident edges. Similarly, a vertex with 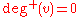 is called a sink.
is called a sink.The degree sum formula states that, for a directed graph,
If for every node ,
 , the graph is called a balanced digraph.
, the graph is called a balanced digraph.Digraph connectivity
A digraph G is called weakly connected (or just connected) if the undirected underlying graph obtained by replacing all directed edges of G with undirected edges is a connected graph. A digraph is strongly connected or strong if it contains a directed path from u to v and a directed path from v to u for every pair of vertices u,v. The strong components are the maximal strongly connected subgraphs.Classes of digraphs
A directed acyclic graphDirected acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
or acyclic digraph is a directed graph with no directed cycles. Special cases of directed acyclic graphs include the multitree
Multitree
In combinatorics and order-theoretic mathematics, a multitree may describe either of two equivalent structures: a directed acyclic graph in which the set of nodes reachable from any node form a tree, or a partially ordered set that does not have four items a, b, c, and d forming a diamond suborder...
s (graphs in which no two directed paths from a single starting node meet back at the same ending node), oriented trees or polytrees (the digraphs formed by orienting the edges of undirected acyclic graphs), and the rooted trees (oriented trees in which all edges of the underlying undirected tree are directed away from the root).
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
.
In the theory of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, a quiver
Quiver (mathematics)
In mathematics, a quiver is a directed graph where loops and multiple arrows between two vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation, V, of a quiver assigns a vector space V to each vertex x of the quiver and a linear map V to each...
Q is a directed graph serving as the domain of, and thus characterizing the shape of, a representation V defined as a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
, specifically an object of the functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
FinVctKF(Q) where F(Q) is the free category on Q consisting of paths in Q and FinVctK is the category of finite dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a field K. Representations of a quiver label its vertices with vector spaces and its edges (and hence paths) compatibly with linear transformations between them, and transform via natural transformations.

