
Harish-Chandra module
Encyclopedia
In mathematics, specifically in the representation theory of Lie groups, a Harish-Chandra
module is a representation of a real Lie group
, associated to a general representation, with regularity and finiteness conditions. When the associated representation is a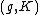 -module, then its Harish-Chandra module is a representation with desirable factorization properties.
-module, then its Harish-Chandra module is a representation with desirable factorization properties.
 is a representation of G, then the Harish-Chandra module of
is a representation of G, then the Harish-Chandra module of  is the vector space X of K-finite
is the vector space X of K-finite
smooth vectors in V. That is, for every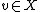 , the map
, the map  via
via
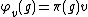
is smooth, and the subspace
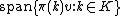
is finite-dimensional.
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
module is a representation of a real Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, associated to a general representation, with regularity and finiteness conditions. When the associated representation is a
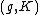 -module, then its Harish-Chandra module is a representation with desirable factorization properties.
-module, then its Harish-Chandra module is a representation with desirable factorization properties.Definition
Let G be a Lie group and K a compact subgroup of G. If is a representation of G, then the Harish-Chandra module of
is a representation of G, then the Harish-Chandra module of  is the vector space X of K-finite
is the vector space X of K-finiteK-finite
In mathematics, a K-finite function is a type of generalized trigonometric polynomial. Here K is some compact group, and the generalization is from the circle group T....
smooth vectors in V. That is, for every
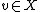 , the map
, the map  via
via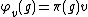
is smooth, and the subspace
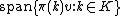
is finite-dimensional.
See also
- (g,K)-module(g,K)-moduleIn mathematics, more specifically in the representation theory of reductive Lie groups, a -module is an algebraic object, first introduced by Harish-Chandra, used to deal with continuous infinite-dimensional representations using algebraic techniques...
- Admissible representationAdmissible representationIn mathematics, admissible representations are a well-behaved class of representations used in the representation theory of reductive Lie groups and locally compact totally disconnected groups. They were introduced by Harish-Chandra....
- Unitary representationUnitary representationIn mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...

