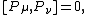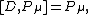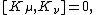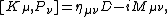Conformal field theory
Encyclopedia
A conformal field theory (CFT) is a quantum field theory
(or statistical mechanics
model at the critical point
) that is invariant
under conformal transformations
. Conformal field theory is often studied in two dimension
s where there is an infinite-dimensional group of local conformal transformations, described by the holomorphic function
s.
Conformal field theory has important applications in string theory
, statistical mechanics
, and condensed matter physics
. The theory was first proposed by Leigh Page
and Norman I. Adams.
to be scale invariant
but not conformally-invariant, examples are rare
. For this reason, the terms are often used interchangeably in the context of quantum field theory, even though the conformal symmetry is larger.
In some particular cases it is possible to prove that scale invariance implies conformal invariance in a quantum field theory, for example in unitary
compact
conformal field theories in two dimensions.
, and the latter to quantum field theory
. The two versions are related by a Wick rotation
.
Two-dimensional CFTs are (in some way) invariant under an infinite-dimensional symmetry group. For example, consider a CFT on the Riemann sphere
. It has the Möbius transformations as the conformal group, which is isomorphic to (the finite-dimensional) PSL(2,C). However, the infinitesimal conformal transformations form an infinite-dimensional algebra, called the Witt algebra
and only the primary fields (or chiral fields) are invariant with respect to the full infinitesimal conformal group.
In most conformal field theories, a conformal anomaly, also known as a Weyl anomaly, arises in the quantum theory. This results in the appearance of a nontrivial central charge, and the Witt algebra
is modified to become the Virasoro algebra
.
In Euclidean CFT, we have a holomorphic and an antiholomorphic copy of the Virasoro algebra. In Lorentzian CFT, we have a left-moving and a right moving copy of the Virasoro algebra (spacetime is a cylinder, with space being a circle, and time a line).
This symmetry makes it possible to classify two-dimensional CFTs much more precisely than in higher dimensions. In particular, it is possible to relate the spectrum of primary operators in a theory to the value of the central charge
, c. The Hilbert space
of physical states is a unitary module
of the Virasoro algebra corresponding to a fixed value of c. Stability requires that the energy spectrum of the Hamiltonian
be nonnegative. The modules of interest are the highest weight modules of the Virasoro algebra.
A chiral field is a holomorphic field W(z) which transforms as
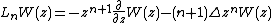
and
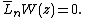
Similarly for an antichiral field. Δ is the conformal weight of the chiral field W.
Furthermore, it was shown by Alexander Zamolodchikov
that there exists a function, C, which decreases monotonically under the renormalization group
flow of a two-dimensional quantum field theory, and is equal to the central charge for a two-dimensional conformal field theory. This is known as the Zamolodchikov C-theorem, and tells us that renormalization group flow in two dimensions is irreversible.
Frequently, we are not just interested in the operators, but we are also interested in the vacuum state, or in statistical mechanics, the thermal state. Unless c=0, there can't possibly be any state which leaves the entire infinite dimensional conformal symmetry unbroken. The best we can come up with is a state which is invariant under L-1, L0, L1, Li,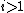
. This contains the Möbius subgroup. The rest of the conformal group is spontaneously broken.
is a symmetry under scale invariance
and under the special conformal transformations having the following relations.
where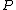
generates translation
s,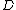
generates scaling transformations as a scalar and 
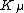generates the special conformal transformations as a covariant vector under Lorentz transformation.
, in which a gravitational theory in anti de Sitter space
(AdS) is equivalent to a conformal field theory on the AdS boundary. Notable examples are d=4 N=4 super-Yang-Mills theory, which is dual to Type IIB string theory on AdS5 x S5, and d=3 N=6 super-Chern-Simons theory
, which is dual to M-theory
on AdS4 x S7. (The prefix "super" denotes supersymmetry
, N denotes the degree of extended supersymmetry possessed by the theory, and d the number of space-time dimensions on the boundary.)
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
(or statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
model at the critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
) that is invariant
Invariant (physics)
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
under conformal transformations
Conformal symmetry
In theoretical physics, conformal symmetry is a symmetry under dilatation and under the special conformal transformations...
. Conformal field theory is often studied in two dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s where there is an infinite-dimensional group of local conformal transformations, described by the holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s.
Conformal field theory has important applications in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, and condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
. The theory was first proposed by Leigh Page
Leigh Page
Leigh Page developed the theory of conformal invariance originally suggested by Harry Bateman...
and Norman I. Adams.
Scale invariance vs. conformal invariance
While it is possible for a quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
to be scale invariant
Scale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
but not conformally-invariant, examples are rare
. For this reason, the terms are often used interchangeably in the context of quantum field theory, even though the conformal symmetry is larger.
In some particular cases it is possible to prove that scale invariance implies conformal invariance in a quantum field theory, for example in unitary
Unitary
Unitary may refer to:* Unitary construction, in automotive design, another common term for a unibody or monocoque construction**Unitary as chemical weapons opposite of Binary...
compact
Compact
Compact as used in politics may refer broadly to a pact or treaty; in more specific cases it may refer to:* Interstate compact* Compact government, a type of colonial rule utilized in British North America...
conformal field theories in two dimensions.
Two-dimensional conformal field theory
There are two versions of 2D CFT: 1) Euclidean, and 2) Lorentzian. The former applies to statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, and the latter to quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. The two versions are related by a Wick rotation
Wick rotation
In physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable...
.
Two-dimensional CFTs are (in some way) invariant under an infinite-dimensional symmetry group. For example, consider a CFT on the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. It has the Möbius transformations as the conformal group, which is isomorphic to (the finite-dimensional) PSL(2,C). However, the infinitesimal conformal transformations form an infinite-dimensional algebra, called the Witt algebra
Witt algebra
In mathematics, the complex Witt algebra, named after Ernst Witt, is the Lie algebra of meromorphic vector fields defined on the Riemann sphere that are holomorphic except at two fixed points. It is also the complexification of the Lie algebra of polynomial vector fields on a circle, and the Lie...
and only the primary fields (or chiral fields) are invariant with respect to the full infinitesimal conformal group.
In most conformal field theories, a conformal anomaly, also known as a Weyl anomaly, arises in the quantum theory. This results in the appearance of a nontrivial central charge, and the Witt algebra
Witt algebra
In mathematics, the complex Witt algebra, named after Ernst Witt, is the Lie algebra of meromorphic vector fields defined on the Riemann sphere that are holomorphic except at two fixed points. It is also the complexification of the Lie algebra of polynomial vector fields on a circle, and the Lie...
is modified to become the Virasoro algebra
Virasoro algebra
In mathematics, the Virasoro algebra is a complex Lie algebra, given as a central extension of the complex polynomial vector fields on the circle, and is widely used in conformal field theory and string theory....
.
In Euclidean CFT, we have a holomorphic and an antiholomorphic copy of the Virasoro algebra. In Lorentzian CFT, we have a left-moving and a right moving copy of the Virasoro algebra (spacetime is a cylinder, with space being a circle, and time a line).
This symmetry makes it possible to classify two-dimensional CFTs much more precisely than in higher dimensions. In particular, it is possible to relate the spectrum of primary operators in a theory to the value of the central charge
Central charge
In theoretical physics, a central charge is an operator Z that commutes with all the other symmetry operators. The adjective "central" refers to the center of the symmetry group -- the subgroup of elements that commute with all other elements of the original group—or to the center of a Lie algebra...
, c. The Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of physical states is a unitary module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
of the Virasoro algebra corresponding to a fixed value of c. Stability requires that the energy spectrum of the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
be nonnegative. The modules of interest are the highest weight modules of the Virasoro algebra.
A chiral field is a holomorphic field W(z) which transforms as
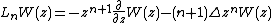
and
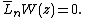
Similarly for an antichiral field. Δ is the conformal weight of the chiral field W.
Furthermore, it was shown by Alexander Zamolodchikov
Alexander Zamolodchikov
Alexander Borissowitsch Zamolodchikov is a Russian physicist, known for his contributions to condensed matter physics and string theory.Born near Dubna,...
that there exists a function, C, which decreases monotonically under the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
flow of a two-dimensional quantum field theory, and is equal to the central charge for a two-dimensional conformal field theory. This is known as the Zamolodchikov C-theorem, and tells us that renormalization group flow in two dimensions is irreversible.
Frequently, we are not just interested in the operators, but we are also interested in the vacuum state, or in statistical mechanics, the thermal state. Unless c=0, there can't possibly be any state which leaves the entire infinite dimensional conformal symmetry unbroken. The best we can come up with is a state which is invariant under L-1, L0, L1, Li,
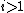. This contains the Möbius subgroup. The rest of the conformal group is spontaneously broken.Conformal symmetry
Conformal symmetryConformal symmetry
In theoretical physics, conformal symmetry is a symmetry under dilatation and under the special conformal transformations...
is a symmetry under scale invariance
Scale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
and under the special conformal transformations having the following relations.
where
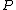generates translationTranslation (physics)
In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...
s,
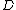generates scaling transformations as a scalar and 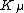generates the special conformal transformations as a covariant vector under Lorentz transformation.Conformal field theory in more than two dimensions
Higher-dimensional conformal field theories are prominent in the AdS/CFT correspondenceAdS/CFT correspondence
In physics, the AdS/CFT correspondence , sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more...
, in which a gravitational theory in anti de Sitter space
Anti de Sitter space
In mathematics and physics, n-dimensional anti de Sitter space, sometimes written AdS_n, is a maximally symmetric Lorentzian manifold with constant negative scalar curvature...
(AdS) is equivalent to a conformal field theory on the AdS boundary. Notable examples are d=4 N=4 super-Yang-Mills theory, which is dual to Type IIB string theory on AdS5 x S5, and d=3 N=6 super-Chern-Simons theory
Chern-Simons theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
, which is dual to M-theory
M-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
on AdS4 x S7. (The prefix "super" denotes supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
, N denotes the degree of extended supersymmetry possessed by the theory, and d the number of space-time dimensions on the boundary.)
See also
- Logarithmic conformal field theoryLogarithmic conformal field theoryIn theoretical physics, a logarithmic conformal field theory is a generalization of the concept of conformal field theory in which the correlators of the basic fields are allowed to be multiply valued and be functions of the logarithm of the separation of the operators.-References:* V. Gurarie, ,...
- AdS/CFT correspondenceAdS/CFT correspondenceIn physics, the AdS/CFT correspondence , sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more...
- Operator product expansionOperator product expansion- 2D Euclidean quantum field theory :In quantum field theory, the operator product expansion is a Laurent series expansion of two operators...
- Vertex operator algebraVertex operator algebraIn mathematics, a vertex operator algebra is an algebraic structure that plays an important role in conformal field theory and related areas of physics...
- WZW model
- critical point
- primary fieldPrimary fieldIn theoretical physics, a primary field is a field operator in quantum field theory - especially conformal field theory or a theory with supersymmetry - that is invariant under the positive frequency modes of the Virasoro algebra - or under one half of the supersymmetries and superconformal...
- superconformal algebraSuperconformal algebraIn theoretical physics, the superconformal algebra is a graded Lie algebra or superalgebra that combines the conformal algebra and supersymmetry. It generates the superconformal group in some cases .In two dimensions, the superconformal algebra is infinite-dimensional...
- Conformal algebra