
Orthogonal complement
Encyclopedia
In the mathematical
fields of linear algebra
and functional analysis
, the orthogonal complement W⊥ of a subspace
W of an inner product space
V is the set of all vectors in V that are orthogonal to every vector in W (Halmos 1974, p. 123):
Informally, it is called the perp, short for perpendicular complement.
s, some subspaces are not closed, but all orthogonal complements are closed. In such spaces, the orthogonal complement of the orthogonal complement of W is the closure
of W, i.e.,
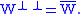
Some other useful properties that always hold are:
The orthogonal complement generalizes to the annihilator
, and gives a Galois connection
on subsets of the inner product space, with associated closure operator
the topological closure of the span.
(n − k)-dimensional subspace, and the double orthogonal complement is the original subspace:

If A is an m × n matrix, where Row A, Col A, and Null A refer to the row space
, column space
, and null space
of A (respectively), we have
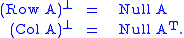
s. In this case one defines the orthogonal complement of W to be a subspace of the dual
of V defined similarly as the annihilator
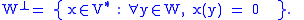
It is always a closed subspace of V∗. There is also an analog of the double complement property. W⊥⊥ is now a subspace of V∗∗ (which is not identical to V). However, the reflexive space
s have a natural
isomorphism
i between V and V∗∗. In this case we have

This is a rather straightforward consequence of the Hahn–Banach theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
fields of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, the orthogonal complement W⊥ of a subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
W of an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
V is the set of all vectors in V that are orthogonal to every vector in W (Halmos 1974, p. 123):

Informally, it is called the perp, short for perpendicular complement.
Properties
The orthogonal complement is always closed in the metric topology. In finite-dimensional spaces, that is merely an instance of the fact that all subspaces of a vector space are closed. In infinite-dimensional Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, some subspaces are not closed, but all orthogonal complements are closed. In such spaces, the orthogonal complement of the orthogonal complement of W is the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of W, i.e.,
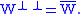
Some other useful properties that always hold are:
- X⊥ =
 ⊥,
⊥, - if Y ⊆ X then X⊥ ⊆ Y⊥,
- X ∩ X⊥ = {0},
- X ⊆ (X⊥)⊥,
- if Y is a closed linear subspace of a Hilbert space, then Y⊥⊥ = Y.
The orthogonal complement generalizes to the annihilator
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
, and gives a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
on subsets of the inner product space, with associated closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
the topological closure of the span.
Finite dimensions
For a finite dimensional inner product space of dimension n, the orthogonal complement of a k-dimensional subspace is an(n − k)-dimensional subspace, and the double orthogonal complement is the original subspace:

If A is an m × n matrix, where Row A, Col A, and Null A refer to the row space
Row space
In linear algebra, the row space of a matrix is the set of all possible linear combinations of its row vectors. The row space of an m × n matrix is a subspace of n-dimensional Euclidean space...
, column space
Column space
In linear algebra, the column space of a matrix is the set of all possible linear combinations of its column vectors. The column space of an m × n matrix is a subspace of m-dimensional Euclidean space...
, and null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of A (respectively), we have
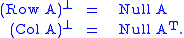
Banach spaces
There is a natural analog of this notion in general Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. In this case one defines the orthogonal complement of W to be a subspace of the dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of V defined similarly as the annihilator
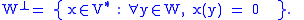
It is always a closed subspace of V∗. There is also an analog of the double complement property. W⊥⊥ is now a subspace of V∗∗ (which is not identical to V). However, the reflexive space
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
s have a natural
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
i between V and V∗∗. In this case we have

This is a rather straightforward consequence of the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
.

