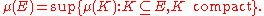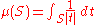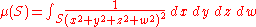Haar measure
Encyclopedia
In mathematical analysis
, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral
for functions on those groups.
This measure
was introduced by Alfréd Haar
, a Hungarian
mathematician
, in 1933. Haar measures are used in many parts of analysis
and number theory
, and also in estimation theory
.
. In this article, the σ-algebra
generated by all compact subsets of G is called the Borel algebra
. An element of the Borel algebra is called a Borel set
. If a is an element of G and S is a subset of G, then we define the left and right translates of S as follows:
Left and right translates map Borel sets into Borel sets.
A measure μ on the Borel subsets of G is called left-translation-invariant if and only if for all Borel subsets S of G and all a in G one has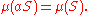
A similar definition is made for right translation invariance.
a positive multiplicative constant, a unique countably additive, nontrivial measure μ on the Borel subsets of G satisfying the following properties:
Such a measure on G is called a left Haar measure. It can be shown as a consequence of the above properties that μ(U) > 0 for every non-empty open subset U. In particular, if G is compact then μ(G) is finite and positive, so we can uniquely specify a left Haar measure on G by adding the normalization condition μ(G) = 1.
The left Haar measure satisfies the inner regularity condition for all σ-finite Borel sets, but may not be inner regular for all Borel sets. For example, the product of the unit circle (with its usual topology) and the real line with the discrete topology is a locally compact group with the product topology and Haar measure on this group is not inner regular for the closed subset {1} x [0,1]. (Compact subsets of this vertical segment are finite sets and points have measure 0, so the measure of any compact subset of this vertical segment is 0. But, using outer regularity, one can show the segment has infinite measure.)
The existence and uniqueness (up to scaling) of a left Haar measure was first proven in full generality by André Weil
. Weil's proof used the axiom of choice and Henri Cartan
furnished a proof which avoided its use. Cartan's proof also proves the existence and the uniqueness simultaneously. The special case of invariant measure for second countable
locally compact groups had been shown by Haar in 1933.
Indeed, for a Borel set S, let us denote by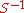
the set of inverses of elements of S. If we define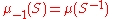
then this is a right Haar measure. To show right invariance, apply the definition:
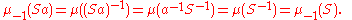
Because the right measure is unique, it follows that μ-1 is a multiple of ν and so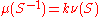
for all Borel sets S, where k is some positive constant.
, one can then define an integral for all Borel measurable functions f on G. This integral is called the Haar integral. If μ is a left Haar measure, then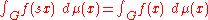
for any integrable function f. This is immediate for step function
s, being essentially the definition of left invariance.
This generalizes to the following:
where m is the Lebesgue measure. The factor (2π)−1 is chosen so that μ(T) = 1.
, of Hilbert's fifth problem
in the case of compact groups. In fact, von Neumann's article was published in the same issue of Annals of Mathematics
as Haar's article and immediately after it.
The Haar measures are used in harmonic analysis
on arbitrary locally compact groups; see Pontryagin duality
. A frequently used technique for proving the existence of a Haar measure on a locally compact group G is showing the existence of a left invariant Radon measure
on G.
In estimation theory
, Haar measures can be used as non-informative priors, being Jeffreys prior
s for various questions. For instance, translation invariance of the (improper) uniform distribution on the real numbers (the Haar measure with respect to addition) corresponds to no information about location, and thus it is the Jeffreys prior for the unknown mean of a Gaussian distribution, the mean being a measure of location.
Unless G is a discrete group, it is impossible to define a countably-additive left invariant measure on all subsets of G, assuming the axiom of choice. See non-measurable set
s.
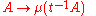
is also right invariant. Thus, there exists a function Δ from the group to the positive reals, called the Haar modulus, modular function or modular character, such that for every Borel set A
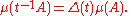
Since right Haar measure is well-defined up to a positive scaling factor, this equation shows the modular function is independent of the choice of right Haar measure in the above equation.
The modular function is a group homomorphism into the multiplicative group of nonzero real numbers. A group is unimodular if and only if the modular function is identically 1. Examples of unimodular groups are abelian group
s, compact group
s, discrete group
s (e.g., finite group
s), semisimple Lie groups and connected nilpotent Lie groups. An example of a non-unimodular group is the ax + b group of transformations of the form
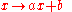
on the real line. This example shows that a solvable Lie group need not be unimodular.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
for functions on those groups.
This measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
was introduced by Alfréd Haar
Alfréd Haar
Alfréd Haar was a Jewish Hungarian mathematician. In 1904 he began to study at the University of Göttingen. His doctorate was supervised by David Hilbert. The Haar measure, Haar wavelet, and Haar transform are named in his honor....
, a Hungarian
Hungary
Hungary , officially the Republic of Hungary , is a landlocked country in Central Europe. It is situated in the Carpathian Basin and is bordered by Slovakia to the north, Ukraine and Romania to the east, Serbia and Croatia to the south, Slovenia to the southwest and Austria to the west. The...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, in 1933. Haar measures are used in many parts of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, and also in estimation theory
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
.
Preliminaries
Let G be a locally compact topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
. In this article, the σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
generated by all compact subsets of G is called the Borel algebra
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
. An element of the Borel algebra is called a Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
. If a is an element of G and S is a subset of G, then we define the left and right translates of S as follows:
- Left translate:
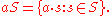
- Right translate:
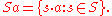
Left and right translates map Borel sets into Borel sets.
A measure μ on the Borel subsets of G is called left-translation-invariant if and only if for all Borel subsets S of G and all a in G one has
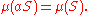
A similar definition is made for right translation invariance.
Haar's theorem
There is, up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a positive multiplicative constant, a unique countably additive, nontrivial measure μ on the Borel subsets of G satisfying the following properties:
- μ(gE) = μ(E) for any g in G and Borel set E (left-translation-invariance).
- μ(K) is finite for every compact set K.
- Every Borel set E is outer regular:
- Every open set E is inner regular:
Such a measure on G is called a left Haar measure. It can be shown as a consequence of the above properties that μ(U) > 0 for every non-empty open subset U. In particular, if G is compact then μ(G) is finite and positive, so we can uniquely specify a left Haar measure on G by adding the normalization condition μ(G) = 1.
The left Haar measure satisfies the inner regularity condition for all σ-finite Borel sets, but may not be inner regular for all Borel sets. For example, the product of the unit circle (with its usual topology) and the real line with the discrete topology is a locally compact group with the product topology and Haar measure on this group is not inner regular for the closed subset {1} x [0,1]. (Compact subsets of this vertical segment are finite sets and points have measure 0, so the measure of any compact subset of this vertical segment is 0. But, using outer regularity, one can show the segment has infinite measure.)
The existence and uniqueness (up to scaling) of a left Haar measure was first proven in full generality by André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
. Weil's proof used the axiom of choice and Henri Cartan
Henri Cartan
Henri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
furnished a proof which avoided its use. Cartan's proof also proves the existence and the uniqueness simultaneously. The special case of invariant measure for second countable
Second-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
locally compact groups had been shown by Haar in 1933.
The right Haar measure
It can also be proved that there exists a unique (up to multiplication by a positive constant) right-translation-invariant Borel measure ν satisfying the above regularity conditions and being finite on compact sets, but it need not coincide with the left-translation-invariant measure μ. The left and right Haar measures are the same only for so-called unimodular groups (see below). It is quite simple, though, to find a relationship between μ and ν.Indeed, for a Borel set S, let us denote by
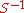the set of inverses of elements of S. If we define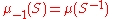then this is a right Haar measure. To show right invariance, apply the definition:
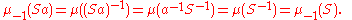
Because the right measure is unique, it follows that μ-1 is a multiple of ν and so
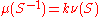
for all Borel sets S, where k is some positive constant.
The Haar integral
Using the general theory of Lebesgue integrationLebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
, one can then define an integral for all Borel measurable functions f on G. This integral is called the Haar integral. If μ is a left Haar measure, then
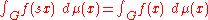
for any integrable function f. This is immediate for step function
Step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
s, being essentially the definition of left invariance.
Examples
- A Haar measure on the topological group (R, +) which takes the value 1 on the interval [0,1] is equal to the restriction of Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
to the Borel subsets of R. This can be generalized to (Rn, +).
- If G is the group of nonzero real numbers with multiplication as operation, then a Haar measure μ is given by
-
- for any Borel subset S of the nonzero reals.
This generalizes to the following:
- For G = GL(n,R), any left Haar measure is a right Haar measure and one such measure μ is given by
-
- where dX denotes the Lebesgue measure on R
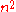, the set of all 
-matrices. This follows from the change of variables formula.
- More generally, on any Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of dimension d a left Haar measure can be associated with any non-zero left-invariant d-form ω, as the Lebesgue measure |ω|; and similarly for right Haar measures. This means also that the modular function can be computed, as the absolute value of the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the adjoint representation.
- More generally, on any Lie group
- In order to define a Haar measure μ on the unit circle T, consider the function f from [0,2π] onto T defined by f(t) = (cos(t),sin(t)). Then μ can be defined by
-
,
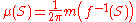where m is the Lebesgue measure. The factor (2π)−1 is chosen so that μ(T) = 1.
- If G is the group of non-null quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, then G can be seen as an open subset of R4. A Haar measure μ is given by
-
- where dx dy dz dw denotes the Lebesgue measure in R4 and S is a Borel subset of G.
Uses
Historically, the first use of the Haar theorem was the solution, by von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, of Hilbert's fifth problem
Hilbert's fifth problem
Hilbert's fifth problem, is the fifth mathematical problem from the problem-list publicized in 1900 by mathematician David Hilbert, and concerns the characterization of Lie groups. The theory of Lie groups describes continuous symmetry in mathematics; its importance there and in theoretical physics...
in the case of compact groups. In fact, von Neumann's article was published in the same issue of Annals of Mathematics
Annals of Mathematics
The Annals of Mathematics is a bimonthly mathematical journal published by Princeton University and the Institute for Advanced Study. It ranks amongst the most prestigious mathematics journals in the world by criteria such as impact factor.-History:The journal began as The Analyst in 1874 and was...
as Haar's article and immediately after it.
The Haar measures are used in harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
on arbitrary locally compact groups; see Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
. A frequently used technique for proving the existence of a Haar measure on a locally compact group G is showing the existence of a left invariant Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
on G.
In estimation theory
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
, Haar measures can be used as non-informative priors, being Jeffreys prior
Jeffreys prior
In Bayesian probability, the Jeffreys prior, named after Harold Jeffreys, is a non-informative prior distribution on parameter space that is proportional to the square root of the determinant of the Fisher information:...
s for various questions. For instance, translation invariance of the (improper) uniform distribution on the real numbers (the Haar measure with respect to addition) corresponds to no information about location, and thus it is the Jeffreys prior for the unknown mean of a Gaussian distribution, the mean being a measure of location.
Unless G is a discrete group, it is impossible to define a countably-additive left invariant measure on all subsets of G, assuming the axiom of choice. See non-measurable set
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
s.
The modular function
The left translate of a right Haar measure is a right Haar measure. More precisely, if μ is a right Haar measure, then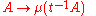is also right invariant. Thus, there exists a function Δ from the group to the positive reals, called the Haar modulus, modular function or modular character, such that for every Borel set A
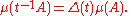
Since right Haar measure is well-defined up to a positive scaling factor, this equation shows the modular function is independent of the choice of right Haar measure in the above equation.
The modular function is a group homomorphism into the multiplicative group of nonzero real numbers. A group is unimodular if and only if the modular function is identically 1. Examples of unimodular groups are abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s, discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
s (e.g., finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s), semisimple Lie groups and connected nilpotent Lie groups. An example of a non-unimodular group is the ax + b group of transformations of the form
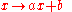
on the real line. This example shows that a solvable Lie group need not be unimodular.
Further reading
- Lynn Loomis, An Introduction to Abstract Harmonic Analysis, D. van Nostrand and Co., 1953.
- André WeilAndré WeilAndré Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, Basic Number Theory, Academic Press, 1971.
External links
- On the Existence and Uniqueness of Invariant Measures on Locally Compact Groups - by Simon Rubinstein-Salzedo