Dimension (vector space)
Encyclopedia
In mathematics
, the dimension of a vector space
V is the cardinality
(i.e. the number of vectors) of a basis
of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension
. This description depends on two fundamental facts: for every vector space there exists a basis (if one assumes the axiom of choice), and all bases of a vector space have equal cardinality (see dimension theorem for vector spaces
); as a result the dimension of a vector space is uniquely defined. The dimension of the vector space V over the field
F can be written as dimF(V) or as [V : F], read "dimension of V over F". When F can be inferred from context, often just dim(V) is written.
We say V is finite-dimensional if the dimension of V is finite.
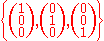
as a basis
, and therefore we have dimR(R3) = 3. More generally, dimR(Rn) = n, and even more generally, dimF(Fn) = n for any field
F.
The complex number
s C are both a real and complex vector space; we have dimR(C) = 2 and dimC(C) = 1. So the dimension depends on the base field.
The only vector space with dimension 0 is {0}, the vector space consisting only of its zero element.
of V, then dim(W) ≤ dim(V).
To show that two finite-dimensional vector spaces are equal, one often uses the following criterion: if V is a finite-dimensional vector space and W is a linear subspace of V with dim(W) = dim(V), then W = V.
Rn has the standard basis {e1, ..., en}, where ei is the i-th column of the corresponding identity matrix
. Therefore Rn
has dimension n.
Any two vector spaces over F having the same dimension are isomorphic. Any bijective map between their bases can be uniquely extended to a bijective linear map between the vector spaces. If B is some set, a vector space with dimension |B| over F can be constructed as follows: take the set F(B) of all functions f : B → F such that f(b) = 0 for all but finitely many b in B. These functions can be added and multiplied with elements of F, and we obtain the desired F-vector space.
An important result about dimensions is given by the rank-nullity theorem
for linear maps.
If F/K is a field extension
, then F is in particular a vector space over K. Furthermore, every F-vector space V is also a K-vector space. The dimensions are related by the formula
In particular, every complex vector space of dimension n is a real vector space of dimension 2n.
Some simple formulae relate the dimension of a vector space with the cardinality of the base field and the cardinality of the space itself.
If V is a vector space over a field F then, denoting the dimension of V by dimV, we have:
, and in the latter there is a well-defined notion of dimension. The length of a module
and the rank of an abelian group
both have several properties similar to the dimension of vector spaces.
The Krull dimension
of a commutative ring, named after Wolfgang Krull
(1899–1971), is defined to be the maximal number of strict inclusions in an increasing chain of prime ideal
s in the ring.
of the identity operator. For instance,
This begs the definition of trace, but allows useful generalizations.
Firstly, it allows one to define a notion of dimension when one has a trace but no natural sense of basis. For example, one may have an algebra A with maps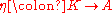
(the inclusion of scalars, called the unit) and a map 
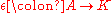(corresponding to trace, called the counit). The composition 
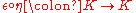is a scalar (being a linear operator on a 1-dimensional space) corresponds to "trace of identity", and gives a notion of dimension for an abstract algebra. In practice, in bialgebra
s one requires that this map be the identity, which can be obtained by normalizing the counit by dividing by dimension (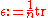
), so in these cases the normalizing constant corresponds to dimension.
Alternatively, one may be able to take the trace of operators on an infinite-dimensional space; in this case a (finite) trace is defined, even though no (finite) dimension exists, and gives a notion of "dimension of the operator". These fall under the rubric of "trace class
operators" on a Hilbert space
, or more generally nuclear operator
s on a Banach space
.
A subtler generalization is to consider the trace of a family of operators as a kind of "twisted" dimension. This occurs significantly in representation theory
, where the character
of a representation is the trace of the representation, hence a scalar-valued function on a group
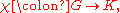whose value on the identity 
is the dimension of the representation, as a representation sends the identity in the group to the identity matrix: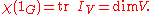 
One can view the other values 
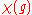of the character as "twisted" dimensions, and find analogs or generalizations of statements about dimensions to statements about characters or representations. A sophisticated example of this occurs in the theory of monstrous moonshine
: the j-invariant
is the graded dimension of an infinite-dimensional graded representation of the Monster group
, and replacing the dimension with the character gives the McKay–Thompson series for each element of the Monster group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the dimension of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V is the cardinality
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
(i.e. the number of vectors) of a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
. This description depends on two fundamental facts: for every vector space there exists a basis (if one assumes the axiom of choice), and all bases of a vector space have equal cardinality (see dimension theorem for vector spaces
Dimension theorem for vector spaces
In mathematics, the dimension theorem for vector spaces states that all bases of a vector space have equally many elements. This number of elements may be finite, or given by an infinite cardinal number, and defines the dimension of the space....
); as a result the dimension of a vector space is uniquely defined. The dimension of the vector space V over the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F can be written as dimF(V) or as [V : F], read "dimension of V over F". When F can be inferred from context, often just dim(V) is written.
We say V is finite-dimensional if the dimension of V is finite.
Examples
The vector space R3 hasas a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, and therefore we have dimR(R3) = 3. More generally, dimR(Rn) = n, and even more generally, dimF(Fn) = n for any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F.
The complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C are both a real and complex vector space; we have dimR(C) = 2 and dimC(C) = 1. So the dimension depends on the base field.
The only vector space with dimension 0 is {0}, the vector space consisting only of its zero element.
Facts
If W is a linear subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of V, then dim(W) ≤ dim(V).
To show that two finite-dimensional vector spaces are equal, one often uses the following criterion: if V is a finite-dimensional vector space and W is a linear subspace of V with dim(W) = dim(V), then W = V.
Rn has the standard basis {e1, ..., en}, where ei is the i-th column of the corresponding identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. Therefore Rn
has dimension n.
Any two vector spaces over F having the same dimension are isomorphic. Any bijective map between their bases can be uniquely extended to a bijective linear map between the vector spaces. If B is some set, a vector space with dimension |B| over F can be constructed as follows: take the set F(B) of all functions f : B → F such that f(b) = 0 for all but finitely many b in B. These functions can be added and multiplied with elements of F, and we obtain the desired F-vector space.
An important result about dimensions is given by the rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
for linear maps.
If F/K is a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
, then F is in particular a vector space over K. Furthermore, every F-vector space V is also a K-vector space. The dimensions are related by the formula
- dimK(V) = dimK(F) dimF(V).
In particular, every complex vector space of dimension n is a real vector space of dimension 2n.
Some simple formulae relate the dimension of a vector space with the cardinality of the base field and the cardinality of the space itself.
If V is a vector space over a field F then, denoting the dimension of V by dimV, we have:
- If dim V is finite, then |V| = |F|dimV.
- If dim V is infinite, then |V| = max(|F|, dimV).
Generalizations
One can see a vector space as a particular case of a matroidMatroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
, and in the latter there is a well-defined notion of dimension. The length of a module
Length of a module
In abstract algebra, the length of a module is a measure of the module's "size". It is defined to be the length of the longest chain of submodules and is a generalization of the concept of dimension for vector spaces...
and the rank of an abelian group
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
both have several properties similar to the dimension of vector spaces.
The Krull dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of a commutative ring, named after Wolfgang Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
(1899–1971), is defined to be the maximal number of strict inclusions in an increasing chain of prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s in the ring.
Trace
The dimension of a vector space may alternatively be characterized as the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the identity operator. For instance,
This begs the definition of trace, but allows useful generalizations.Firstly, it allows one to define a notion of dimension when one has a trace but no natural sense of basis. For example, one may have an algebra A with maps
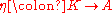(the inclusion of scalars, called the unit) and a map 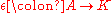(corresponding to trace, called the counit). The composition 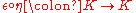is a scalar (being a linear operator on a 1-dimensional space) corresponds to "trace of identity", and gives a notion of dimension for an abstract algebra. In practice, in bialgebraBialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
s one requires that this map be the identity, which can be obtained by normalizing the counit by dividing by dimension (
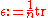), so in these cases the normalizing constant corresponds to dimension.Alternatively, one may be able to take the trace of operators on an infinite-dimensional space; in this case a (finite) trace is defined, even though no (finite) dimension exists, and gives a notion of "dimension of the operator". These fall under the rubric of "trace class
Trace class
In mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
operators" on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, or more generally nuclear operator
Nuclear operator
In mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
s on a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
A subtler generalization is to consider the trace of a family of operators as a kind of "twisted" dimension. This occurs significantly in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, where the character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
of a representation is the trace of the representation, hence a scalar-valued function on a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
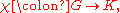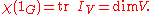whose value on the identity is the dimension of the representation, as a representation sends the identity in the group to the identity matrix: One can view the other values of the character as "twisted" dimensions, and find analogs or generalizations of statements about dimensions to statements about characters or representations. A sophisticated example of this occurs in the theory of monstrous moonshineMonstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
: the j-invariant
J-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
is the graded dimension of an infinite-dimensional graded representation of the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
, and replacing the dimension with the character gives the McKay–Thompson series for each element of the Monster group.
See also
- Basis (linear algebra)Basis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
- Topological dimension, also called Lebesgue covering dimension
- Fractal dimensionFractal dimensionIn fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
, also called Hausdorff dimension - Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
External links
- MIT Linear Algebra Lecture on Independence, Basis, and Dimension by Gilbert Strang at MIT OpenCourseWare