
Levi decomposition
Encyclopedia
In Lie theory
and representation theory
, the Levi decomposition, conjectured by Killing and Cartan and proved by , states that any finite dimensional real Lie algebra
g is the semidirect product of a solvable ideal and a semisimple subalgebra.
of a solvable Lie algebra and a semisimple Lie algebra.
When viewed as a factor-algebra of g, this semisimple Lie algebra is also called the Levi factor of g. Moreover, Malcev (1942) showed that any two Levi subalgebras are conjugate by an (inner) automorphism of the form
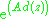
where z is in the nilradical (Levi–Malcev theorem).
representations. The Langlands decomposition
is a slight refinement of the Levi decomposition for parabolic subgroups used in this context.
Analogous statements hold for simply connected Lie group
s, and, as shown by George Mostow
, for algebraic Lie algebras and simply connected algebraic group
s over a field of characteristic
zero.
There is no analogue of the Levi decomposition for most infinite-dimensional Lie algebras; for example affine Lie algebra
s have a radical consisting of their center, but cannot be written as a semidirect product of the center and another Lie algebra. The Levi decomposition also fails for finite dimensional algebras over fields of positive characteristic.
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
and representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, the Levi decomposition, conjectured by Killing and Cartan and proved by , states that any finite dimensional real Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
g is the semidirect product of a solvable ideal and a semisimple subalgebra.
Formal statement
One is its radical, a maximal solvable ideal, and the other is a semisimple subalgebra, called a Levi subalgebra. Levi decomposition implies that any finite dimensional Lie algebra is a semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of a solvable Lie algebra and a semisimple Lie algebra.
When viewed as a factor-algebra of g, this semisimple Lie algebra is also called the Levi factor of g. Moreover, Malcev (1942) showed that any two Levi subalgebras are conjugate by an (inner) automorphism of the form
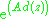
where z is in the nilradical (Levi–Malcev theorem).
Application
To a certain extent, the decomposition can be used to reduce problems about finite dimensional Lie algebras and Lie groups to separate problems about Lie algebras in these two special classes, solvable and semisimple.Extensions of the results
In representation theory, Levi decomposition of parabolic subgroups of a reductive group is needed to construct a large family of the so-called parabolically inducedParabolic induction
In mathematics, parabolic induction is a method of constructing representations of a reductive group from representations of its parabolic subgroups....
representations. The Langlands decomposition
Langlands decomposition
In mathematics, the Langlands decomposition writes a parabolic subgroup P of a semisimple Lie group as a product P=MAN of a reductive subgroup M, an abelian subgroup A, and a nilpotent subgroup N.- Applications :...
is a slight refinement of the Levi decomposition for parabolic subgroups used in this context.
Analogous statements hold for simply connected Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, and, as shown by George Mostow
George Mostow
George Mostow is an American mathematician, a member of the National Academy of Sciences, Henry Ford II Professor of Mathematics at Yale University, the 49th President of the American Mathematical Society ,...
, for algebraic Lie algebras and simply connected algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s over a field of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero.
There is no analogue of the Levi decomposition for most infinite-dimensional Lie algebras; for example affine Lie algebra
Affine Lie algebra
In mathematics, an affine Lie algebra is an infinite-dimensional Lie algebra that is constructed in a canonical fashion out of a finite-dimensional simple Lie algebra. It is a Kac–Moody algebra for which the generalized Cartan matrix is positive semi-definite and has corank 1...
s have a radical consisting of their center, but cannot be written as a semidirect product of the center and another Lie algebra. The Levi decomposition also fails for finite dimensional algebras over fields of positive characteristic.

