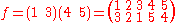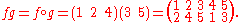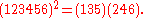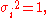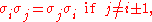Symmetric group
Encyclopedia
In mathematics, the symmetric group Sn on a finite set of n symbols is the group
whose elements are all the permutations of the n symbols, and whose group operation is the composition
of such permutations, which are treated as bijective functions
from the set of symbols to itself. Since there are n!
(n factorial
) possible permutations of a set of n symbols, it follows that the order
(the number of elements) of the symmetric group Sn is n!.
Although symmetric groups can be defined on infinite sets as well, this article discusses only the finite symmetric groups: their applications, their elements, their conjugacy class
es, a finite presentation, their subgroup
s, their automorphism groups, and their representation theory. For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set.
The symmetric group is important to diverse areas of mathematics such as Galois theory
, invariant theory
, the representation theory of Lie groups, and combinatorics
. Cayley's theorem
states that every group G is isomorphic
to a subgroup
of the symmetric group on G.
. For finite sets, "permutations" and "bijective functions" refer to the same operation, namely rearrangement. The symmetric group of degree n is the symmetric group on the set X = { 1, 2, ..., n }.
The symmetric group on a set X is denoted in various ways including SX, , ΣX, and Sym(X). If X is the set { 1, 2, ..., n }, then the symmetric group on X is also denoted Sn,
, ΣX, and Sym(X). If X is the set { 1, 2, ..., n }, then the symmetric group on X is also denoted Sn,  Σn, and Sym(n).
Σn, and Sym(n).
Symmetric groups on infinite sets behave quite differently than symmetric groups on finite sets, and are discussed in , , and . This article concentrates on the finite symmetric groups.
The symmetric group on a set of n elements has order
n!
It is abelian
if and only if . For n = 0 and n = 1 (the empty set
and the singleton set) the symmetric group is trivial
(note that this agrees with 0! = 1! = 1), and in these cases the alternating group equals the symmetric group, rather than being an index two subgroup. The group Sn is solvable
if and only if . This is an essential part of the proof of the Abel–Ruffini theorem
that shows that for every there are polynomial
s of degree n which are not solvable by radicals, i.e., the solutions cannot be expressed by performing a finite number of operations of addition, subtraction, multiplication, division and root extraction on the polynomial's coefficients.
of the general polynomial
of degree n and plays an important role in Galois theory
. In invariant theory
, the symmetric group acts on the variables of a multi-variate function, and the functions left invariant are the so-called symmetric function
s. In the representation theory of Lie groups, the representation theory of the symmetric group
plays a fundamental role through the ideas of Schur functor
s. In the theory of Coxeter group
s, the symmetric group is the Coxeter group of type An and occurs as the Weyl group
of the general linear group
. In combinatorics
, the symmetric groups, their elements (permutation
s), and their representations
provide a rich source of problems involving Young tableaux, plactic monoid
s, and the Bruhat order
. Subgroup
s of symmetric groups are called permutation group
s and are widely studied because of their importance in understanding group action
s, homogenous spaces, and automorphism groups of graph
s, such as the Higman–Sims group and the Higman–Sims graph.
s of X.
, denoted by the symbol or simply by juxtaposition of the permutations. The composition
or simply by juxtaposition of the permutations. The composition  of permutations f and g, pronounced "f after g", maps any element x of X to f(g(x)). Concretely, let
of permutations f and g, pronounced "f after g", maps any element x of X to f(g(x)). Concretely, let
and
Applying f after g maps 1 first to 2 and then 2 to itself; 2 to 5 and then to 4; 3 to 4 and then to 5, and so on. So composing f and g gives
A cycle
of length L = k·m, taken to the k-th power, will decompose into k cycles of length m: For example (k = 2, m = 3),
, it is necessary to verify the group axioms of associativity, identity, and inverses. The operation of function composition
is always associative. The trivial bijection that assigns each element of X to itself serves as an identity for the group. Every bijection has an inverse function
that undoes its action, and thus each element of a symmetric group does have an inverse.
, whereas f is an even permutation.
The representation of a permutation as a product of transpositions is not unique; however, the number of transpositions needed to represent a given permutation is either always even or always odd. There are several short proofs of the invariance of this parity of a permutation.
The product of two even permutations is even, the product of two odd permutations is even, and all other products are odd. Thus we can define the sign of a permutation:

With this definition,
is a group homomorphism
({+1, –1} is a group under multiplication, where +1 is e, the neutral element). The kernel
of this homomorphism, i.e. the set of all even permutations, is called the alternating group An. It is a normal subgroup
of Sn, and for n ≥ 2 it has n! / 2 elements. The group Sn is the semidirect product
of An and any subgroup generated by a single transposition.
Furthermore, every permutation can be written as a product of adjacent transpositions, that is, transpositions of the form . For instance, the permutation g from above can also be written as g = (4 5)(3 4)(4 5)(1 2)(2 3)(3 4)(4 5). The representation of a permutation as a product of adjacent transpositions is also not unique.
. For instance, the permutation g from above can also be written as g = (4 5)(3 4)(4 5)(1 2)(2 3)(3 4)(4 5). The representation of a permutation as a product of adjacent transpositions is also not unique.
of length k is a permutation f for which there exists an element x in {1,...,n} such that x, f(x), f2(x), ..., fk(x) = x are the only elements moved by f; it is required that k ≥ 2 since with k = 1 the element x itself would not be moved either. The permutation h defined by

is a cycle of length three, since h(1) = 4, h(4) = 3 and h(3) = 1, leaving 2 and 5 untouched. We denote such a cycle by (1 4 3), but it could equally well be written (4 3 1) or (3 1 4) by starting at a different point. The order of a cycle is equal to its length. Cycles of length two are transpositions. Two cycles are disjoint if they move disjoint subsets of elements. Disjoint cycles commute, e.g. in S6 we have (4 1 3)(2 5 6) = (2 5 6)(4 1 3). Every element of Sn can be written as a product of disjoint cycles; this representation is unique up to
the order of the factors, and the freedom present in representing each individual cycle by choosing its starting point.
The is the one given by: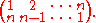
This is the unique maximal element with respect to the Bruhat order
and the
longest element
in the symmetric group with respect to generating set consisting of the adjacent transpositions (i i+1), 1 ≤ i ≤ n − 1.
This is an involution, and consists of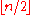 (non-adjacent) transpositions
(non-adjacent) transpositions
so it thus has sign:

which is 4-periodic in n.
In , the perfect shuffle is the permutation that splits the set into 2 piles and interleaves them. Its sign is also
, the perfect shuffle is the permutation that splits the set into 2 piles and interleaves them. Its sign is also 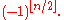
Note that the reverse on n elements and perfect shuffle on 2n elements have the same sign; these are important to the classification of Clifford algebra
s, which are 8-periodic.
es of Sn correspond to the cycle structures of permutations; that is, two elements of Sn are conjugate in Sn if and only if they consist of the same number of disjoint cycles of the same lengths.
For instance, in S5, (1 2 3)(4 5) and (1 4 3)(2 5) are conjugate; (1 2 3)(4 5) and (1 2)(4 5) are not.
A conjugating element of Sn can be constructed in "two line notation" by placing the "cycle notations" of the two conjugate permutations on top of one another. Continuing the previous example:
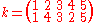
which can be written as the product of cycles, namely:
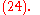
This permutation then relates (1 2 3)(4 5) and (1 4 3)(2 5) via conjugation, i.e.

It is clear that such a permutation is not unique.
Sym(0) and Sym(1): The symmetric groups on the empty set
and the singleton set are trivial, which corresponds to 0! = 1! = 1. In this case the alternating group agrees with the symmetric group, rather than being an index 2 subgroup, and the sign map is trivial.
Sym(2): The symmetric group on two points consists of exactly two elements: the identity and the permutation swapping the two points. It is a cyclic group
and so abelian
. In Galois theory
, this corresponds to the fact that the quadratic formula gives a direct solution to the general quadratic polynomial
after extracting only a single root. In invariant theory
, the representation theory of the symmetric group on two points is quite simple and is seen as writing a function of two variables as a sum of its symmetric and anti-symmetric parts: Setting fs(x,y) = f(x,y) + f(y,x), and fa(x,y) = f(x,y) − f(y,x), one gets that 2·f = fs + fa. This process is known as symmetrization
.
Sym(3): is isomorphic to the dihedral group of order 6
, the group of reflection and rotation symmetries of an equilateral triangle, since these symmetries permute the three vertices of the triangle. Cycles of length two correspond to reflections, and cycles of length three are rotations. In Galois theory, the sign map from Sym(3) to Sym(2) corresponds to the resolving quadratic for a cubic polynomial, as discovered by Gerolamo Cardano
, while the Alt(3) kernel corresponds to the use of the discrete Fourier transform
of order 3 in the solution, in the form of Lagrange resolvents.
Sym(4): The group S4 is isomorphic to the group of proper rotations about opposite faces, opposite diagonals and opposite edges, 9, 8 and 6 permutations, of the cube
. Beyond the group Alt(4), Sym(4) has a Klein four-group
V as a proper normal subgroup
, namely the even transpositions {(1), (12)(34), (13)(24), (14)(23)}, with quotient Sym(3). In Galois theory
, this map corresponds to the resolving cubic to a quartic polynomial, which allows the quartic to be solved by radicals, as established by Lodovico Ferrari
. The Klein group can be understood in terms of the Lagrange resolvents of the quartic. The map from Sym(4) to Sym(3) also yields a 2-dimensional irreducible representation, which is an irreducible representation of a symmetric group of degree n of dimension below n−1, which only occurs for n=4.
Sym(5): Sym(5) is the first non-solvable symmetric group. Along with the special linear group
SL(2,5) and the icosahedral group Alt(5) × Sym(2), Sym(5) is one of the three non-solvable groups of order 120 up to isomorphism. Sym(5) is the Galois group
of the general quintic equation
, and the fact that Sym(5) is not a solvable group
translates into the non-existence of a general formula to solve quintic polynomials by radicals. There is an exotic inclusion map as a transitive subgroup; the obvious inclusion map
as a transitive subgroup; the obvious inclusion map  fixes a point and thus is not transitive. This yields the outer automorphism of
fixes a point and thus is not transitive. This yields the outer automorphism of 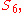 discussed below, and corresponds to the resolvent sextic of a quintic.
discussed below, and corresponds to the resolvent sextic of a quintic.
Sym(6): Sym(6), unlike other symmetric groups, has an outer automorphism. Using the language of Galois theory
, this can also be understood in terms of Lagrange resolvents. The resolvent of a quintic is of degree 6—this corresponds to an exotic inclusion map as a transitive subgroup (the obvious inclusion map
as a transitive subgroup (the obvious inclusion map  fixes a point and thus is not transitive) and, while this map does not make the general quintic solvable, it yields the exotic outer automorphism of
fixes a point and thus is not transitive) and, while this map does not make the general quintic solvable, it yields the exotic outer automorphism of 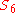 —see automorphisms of the symmetric and alternating groups for details.
—see automorphisms of the symmetric and alternating groups for details.
 and the sign map
and the sign map  the notable maps between symmetric groups, in order of relative dimension
the notable maps between symmetric groups, in order of relative dimension
, are:
s and reflection group
s. They can be realized as a group of reflections with respect to hyperplanes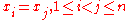 . Braid group
. Braid group
s Bn admit symmetric groups Sn as quotient group
s.
Cayley's theorem
states that every group G is isomorphic to a subgroup of the symmetric group on the elements of G, as a group acts on itself faithfully by (left or right) multiplication.
, and the induced quotient is the sign map: which is split by taking a transposition of two elements. Thus Sn is the semidirect product
which is split by taking a transposition of two elements. Thus Sn is the semidirect product  and has no other proper normal subgroups, as they would intersect An in either the identity (and thus themselves be the identity or a 2-element group, which is not normal), or in An (and thus themselves be An or Sn).
and has no other proper normal subgroups, as they would intersect An in either the identity (and thus themselves be the identity or a 2-element group, which is not normal), or in An (and thus themselves be An or Sn).
Sn acts on its subgroup An by conjugation, and for n ≠ 6, Sn is the full automorphism group of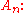
 Conjugation by even elements are inner automorphism
Conjugation by even elements are inner automorphism
s of An while the outer automorphism of An of order 2 corresponds to conjugation by an odd element. For n = 6, there is an exceptional outer automorphism of An so Sn is not the full automorphism group of An.
Conversely, for n ≠ 6, Sn has no outer automorphisms, and for n ≠ 2 it has no center, so for n ≠ 2, 6 it is a complete group
, as discussed in automorphism group, below.
For n ≥ 5, Sn is an almost simple group
, as it lies between the simple group An and its group of automorphisms.
 and relations:
and relations:
One thinks of as swapping the i-th and i+1-st position.
as swapping the i-th and i+1-st position.
Other popular generating sets include the set of transpositions that swap 1 and i for 2 ≤ i ≤ n and any set containing an n-cycle and a 2-cycle.
s of the finite symmetric groups are well understood. If n ≤ 2, Sn has at most 2 elements, and so has no nontrivial proper subgroups. The alternating group of degree n is always a normal subgroup, a proper one for n ≥ 2 and nontrivial for n ≥ 3; for n ≥ 3 it is in fact the only non-identity proper normal subgroup of Sn, except when n = 4 where there is one additional such normal subgroup, which is isomorphic to the Klein four group.
The symmetric group on an infinite set does not have an associated alternating group: not all elements can be written as a (finite) product of transpositions. However it does contain a normal subgroup S of permutations that fix all but finitely many elements, and such permutations can be classified as either even or odd. The even elements of S form the alternating subgroup A of S, and since A is even a characteristic subgroup
of S, it is also a normal subgroup of the full symmetric group of the infinite set. The groups A and S are the only non-identity proper normal subgroups of the symmetric group on a countably infinite set. For more details see or .
s of the finite symmetric groups fall into three classes: the intransitive, the imprimitive, and the primitive. The intransitive maximal subgroups are exactly those of the form Sym(k) × Sym(n−k) for 1 ≤ k < n/2. The imprimitive maximal subgroups are exactly those of the form Sym(k) wr Sym( n/k ) where 2 ≤ k ≤ n/2 is a proper divisor of n and "wr" denotes the wreath product
acting imprimitively. The primitive maximal subgroups are more difficult to identify, but with the assistance of the O'Nan–Scott theorem and the classification of finite simple groups
, gave a fairly satisfactory description of the maximal subgroups of this type according to .
. They are more easily described in special cases first:
The Sylow p-subgroups of the symmetric group of degree p are just the cyclic subgroups generated by p-cycles. There are (p − 1)!/(p − 1) = (p − 2)! such subgroups simply by counting generators. The normalizer therefore has order p·(p − 1) and is known as a Frobenius group
Fp(p − 1) (especially for p = 5), and as the affine general linear group, AGL(1, p).
The Sylow p-subgroups of the symmetric group of degree p2 are the wreath product
of two cyclic groups of order p. For instance, when p = 3, a Sylow 3-subgroup of Sym(9) is generated by a = (1, 4, 7)(2, 5, 8)(3, 6, 9) and the elements x = (1,2,3), y = (4, 5, 6), z = (7, 8, 9), and every element of the Sylow 3-subgroup has the form aixjykzl for 0 ≤ i,j,k,l ≤ 2.
The Sylow p-subgroups of the symmetric group of degree pn are sometimes denoted Wp(n), and using this notation one has that Wp(n + 1) is the wreath product of Wp(n) and Wp(1).
In general, the Sylow p-subgroups of the symmetric group of degree n are a direct product of ai copies of Wp(i), where 0 ≤ ai ≤ p − 1 and n = a0 + p·a1 + ... + pk·ak.
For instance, W2(1) = C2 and W2(2) = D8, the dihedral group of order 8, and so a Sylow 2-subgroup of the symmetric group of degree 7 is generated by { (1,3)(2,4), (1,2), (3,4), (5,6) } and is isomorphic to D8 × C2.
These calculations are attributed to and described in more detail in . Note however that attributes the result to an 1844 work of Cauchy, and mentions that it is even covered in textbook form in .
is a transitive subgroup of Sn, for some n.
For ,
,  is a complete group
is a complete group
: its center
and outer automorphism group
are both trivial.
For n = 2, the automorphism group is trivial, but is not trivial: it is isomorphic to
is not trivial: it is isomorphic to 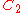 , which is abelian, and hence the center is the whole group.
, which is abelian, and hence the center is the whole group.
For n = 6, it has an outer automorphism of order 2: , and the automorphism group is a semidirect product
, and the automorphism group is a semidirect product
In fact, for any set X of cardinality other than 6, every automorphism of the symmetric group on X is inner, a result first due to according to .
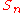 is quite regular and stabilizes: the first homology (concretely, the abelianization) is:
is quite regular and stabilizes: the first homology (concretely, the abelianization) is:

The first homology group is the abelianization, and corresponds to the sign map which is the abelianization for n ≥ 2; for n < 2 the symmetric group is trivial. This homology is easily computed as follows: Sn is generated by involutions (2-cycles, which have order 2), so the only non-trivial maps
which is the abelianization for n ≥ 2; for n < 2 the symmetric group is trivial. This homology is easily computed as follows: Sn is generated by involutions (2-cycles, which have order 2), so the only non-trivial maps  are to
are to  and all involutions are conjugate, hence map to the same element in the abelianization (since conjugation is trivial in abelian groups). Thus the only possible maps
and all involutions are conjugate, hence map to the same element in the abelianization (since conjugation is trivial in abelian groups). Thus the only possible maps  send an involution to 1 (the trivial map) or to −1 (the sign map). One must also show that the sign map is well-defined, but assuming that, this gives the first homology of Sn.
send an involution to 1 (the trivial map) or to −1 (the sign map). One must also show that the sign map is well-defined, but assuming that, this gives the first homology of Sn.
The second homology (concretely, the Schur multiplier
) is:
This was computed in , and corresponds to the double cover of the symmetric group
, 2 · Sn.
Note that the exceptional
low-dimensional homology of the alternating group ( corresponding to non-trivial abelianization, and
corresponding to non-trivial abelianization, and  due to the exceptional 3-fold cover) does not change the homology of the symmetric group; the alternating group phenomena do yield symmetric group phenomena – the map
due to the exceptional 3-fold cover) does not change the homology of the symmetric group; the alternating group phenomena do yield symmetric group phenomena – the map  extends to
extends to  and the triple covers of
and the triple covers of 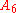 and
and  extend to triple covers of
extend to triple covers of 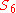 and
and  – but these are not homological – the map
– but these are not homological – the map  does not change the abelianization of
does not change the abelianization of  and the triple covers do not correspond to homology either.
and the triple covers do not correspond to homology either.
The homology "stabilizes" in the sense of stable homotopy theory: there is an inclusion map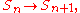 and for fixed k, the induced map on homology
and for fixed k, the induced map on homology 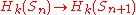 is an isomorphism for sufficiently high n. This is analogous to the homology of families Lie groups stabilizing.
is an isomorphism for sufficiently high n. This is analogous to the homology of families Lie groups stabilizing.
The homology of the infinite symmetric group is computed in , with the cohomology algebra forming a Hopf algebra
.
is a particular case of the representation theory of finite groups
, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function
theory to problems of quantum mechanics
for a number of identical particles
.
The symmetric group Sn has order n! . Its conjugacy class
es are labeled by partitions of n. Therefore according to the representation theory of a finite group, the number of inequivalent irreducible representations, over the complex number
s, is equal to the number of partitions of n. Unlike the general situation for finite groups, there is in fact a natural way to parametrize irreducible representation by the same set that parametrizes conjugacy classes, namely by partitions of n or equivalently Young diagrams of size n.
Each such irreducible representation can be realized over the integers (every permutation acting by a matrix with integer coefficients); it can be explicitly constructed by computing the Young symmetrizer
s acting on a space generated by the Young tableau
x of shape given by the Young diagram.
Over other field
s the situation can become much more complicated. If the field K has characteristic
equal to zero or greater than n then by Maschke's theorem
the group algebra
KSn is semisimple. In these cases the irreducible representations defined over the integers give the complete set of irreducible representations (after reduction modulo the characteristic if necessary).
However, the irreducible representations of the symmetric group are not known in arbitrary characteristic. In this context it is more usual to use the language of module
s rather than representations. The representation obtained from an irreducible representation defined over the integers by reducing modulo the characteristic will not in general be irreducible. The modules so constructed are called Specht modules, and every irreducible does arise inside some such module. There are now fewer irreducibles, and although they can be classified they are very poorly understood. For example, even their dimension
s are not known in general.
The determination of the irreducible modules for the symmetric group over an arbitrary field is widely regarded as one of the most important open problems in representation theory.
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
whose elements are all the permutations of the n symbols, and whose group operation is the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of such permutations, which are treated as bijective functions
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from the set of symbols to itself. Since there are n!
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
(n factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
) possible permutations of a set of n symbols, it follows that the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
(the number of elements) of the symmetric group Sn is n!.
Although symmetric groups can be defined on infinite sets as well, this article discusses only the finite symmetric groups: their applications, their elements, their conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es, a finite presentation, their subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s, their automorphism groups, and their representation theory. For the remainder of this article, "symmetric group" will mean a symmetric group on a finite set.
The symmetric group is important to diverse areas of mathematics such as Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
, the representation theory of Lie groups, and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
. Cayley's theorem
Cayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
states that every group G is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the symmetric group on G.
Definition and first properties
The symmetric group on a finite set X is the group whose elements are all bijective functions from X to X and whose group operation is that of function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. For finite sets, "permutations" and "bijective functions" refer to the same operation, namely rearrangement. The symmetric group of degree n is the symmetric group on the set X = { 1, 2, ..., n }.
The symmetric group on a set X is denoted in various ways including SX,
 , ΣX, and Sym(X). If X is the set { 1, 2, ..., n }, then the symmetric group on X is also denoted Sn,
, ΣX, and Sym(X). If X is the set { 1, 2, ..., n }, then the symmetric group on X is also denoted Sn,  Σn, and Sym(n).
Σn, and Sym(n).Symmetric groups on infinite sets behave quite differently than symmetric groups on finite sets, and are discussed in , , and . This article concentrates on the finite symmetric groups.
The symmetric group on a set of n elements has order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
n!
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
It is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
if and only if . For n = 0 and n = 1 (the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and the singleton set) the symmetric group is trivial
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
(note that this agrees with 0! = 1! = 1), and in these cases the alternating group equals the symmetric group, rather than being an index two subgroup. The group Sn is solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
if and only if . This is an essential part of the proof of the Abel–Ruffini theorem
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
that shows that for every there are polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s of degree n which are not solvable by radicals, i.e., the solutions cannot be expressed by performing a finite number of operations of addition, subtraction, multiplication, division and root extraction on the polynomial's coefficients.
Applications
The symmetric group on a set of size n is the Galois groupGalois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the general polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of degree n and plays an important role in Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
. In invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
, the symmetric group acts on the variables of a multi-variate function, and the functions left invariant are the so-called symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s. In the representation theory of Lie groups, the representation theory of the symmetric group
Representation theory of the symmetric group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to problems of quantum...
plays a fundamental role through the ideas of Schur functor
Schur functor
In mathematics, especially in the field of representation theory, a Schur functor is a functor from the category of modules over a fixed commutative ring to itself. Schur functors are indexed by partitions and are described as follows. Let R be a commutative ring, E an R moduleand λ a partition of...
s. In the theory of Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s, the symmetric group is the Coxeter group of type An and occurs as the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
. In combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the symmetric groups, their elements (permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s), and their representations
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
provide a rich source of problems involving Young tableaux, plactic monoid
Plactic monoid
In mathematics, the plactic monoid is the monoid of all words in the alphabet of positive integers modulo Knuth equivalence. Its elements can be identified with semistandard Young tableaux...
s, and the Bruhat order
Bruhat order
In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
. Subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of symmetric groups are called permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s and are widely studied because of their importance in understanding group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s, homogenous spaces, and automorphism groups of graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s, such as the Higman–Sims group and the Higman–Sims graph.
Elements
The elements of the symmetric group on a set X are the permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of X.
Multiplication
The group operation in a symmetric group is function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, denoted by the symbol
 or simply by juxtaposition of the permutations. The composition
or simply by juxtaposition of the permutations. The composition  of permutations f and g, pronounced "f after g", maps any element x of X to f(g(x)). Concretely, let
of permutations f and g, pronounced "f after g", maps any element x of X to f(g(x)). Concretely, let
and
-
 (See permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
(See permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
for an explanation of notation).
Applying f after g maps 1 first to 2 and then 2 to itself; 2 to 5 and then to 4; 3 to 4 and then to 5, and so on. So composing f and g gives
A cycle
Cycle (mathematics)
In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
of length L = k·m, taken to the k-th power, will decompose into k cycles of length m: For example (k = 2, m = 3),
Verification of group axioms
To check that the symmetric group on a set X is indeed a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, it is necessary to verify the group axioms of associativity, identity, and inverses. The operation of function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
is always associative. The trivial bijection that assigns each element of X to itself serves as an identity for the group. Every bijection has an inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
that undoes its action, and thus each element of a symmetric group does have an inverse.
Transpositions
A transposition is a permutation which exchanges two elements and keeps all others fixed; for example (1 3) is a transposition. Every permutation can be written as a product of transpositions; for instance, the permutation g from above can be written as g = (1 5)(1 2)(3 4). Since g can be written as a product of an odd number of transpositions, it is then called an odd permutationEven and odd permutations
In mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
, whereas f is an even permutation.
The representation of a permutation as a product of transpositions is not unique; however, the number of transpositions needed to represent a given permutation is either always even or always odd. There are several short proofs of the invariance of this parity of a permutation.
The product of two even permutations is even, the product of two odd permutations is even, and all other products are odd. Thus we can define the sign of a permutation:

With this definition,

is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
({+1, –1} is a group under multiplication, where +1 is e, the neutral element). The kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of this homomorphism, i.e. the set of all even permutations, is called the alternating group An. It is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of Sn, and for n ≥ 2 it has n! / 2 elements. The group Sn is the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of An and any subgroup generated by a single transposition.
Furthermore, every permutation can be written as a product of adjacent transpositions, that is, transpositions of the form
 . For instance, the permutation g from above can also be written as g = (4 5)(3 4)(4 5)(1 2)(2 3)(3 4)(4 5). The representation of a permutation as a product of adjacent transpositions is also not unique.
. For instance, the permutation g from above can also be written as g = (4 5)(3 4)(4 5)(1 2)(2 3)(3 4)(4 5). The representation of a permutation as a product of adjacent transpositions is also not unique.Cycles
A cycleCycle (mathematics)
In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
of length k is a permutation f for which there exists an element x in {1,...,n} such that x, f(x), f2(x), ..., fk(x) = x are the only elements moved by f; it is required that k ≥ 2 since with k = 1 the element x itself would not be moved either. The permutation h defined by

is a cycle of length three, since h(1) = 4, h(4) = 3 and h(3) = 1, leaving 2 and 5 untouched. We denote such a cycle by (1 4 3), but it could equally well be written (4 3 1) or (3 1 4) by starting at a different point. The order of a cycle is equal to its length. Cycles of length two are transpositions. Two cycles are disjoint if they move disjoint subsets of elements. Disjoint cycles commute, e.g. in S6 we have (4 1 3)(2 5 6) = (2 5 6)(4 1 3). Every element of Sn can be written as a product of disjoint cycles; this representation is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
the order of the factors, and the freedom present in representing each individual cycle by choosing its starting point.
Special elements
Certain elements of the symmetric group of {1,2, ..., n} are of particular interest (these can be generalized to the symmetric group of any finite totally ordered set, but not to that of an unordered set).The is the one given by:
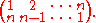
This is the unique maximal element with respect to the Bruhat order
Bruhat order
In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
and the
longest element
Longest element of a Coxeter group
In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
in the symmetric group with respect to generating set consisting of the adjacent transpositions (i i+1), 1 ≤ i ≤ n − 1.
This is an involution, and consists of
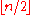 (non-adjacent) transpositions
(non-adjacent) transpositions
so it thus has sign:

which is 4-periodic in n.
In
 , the perfect shuffle is the permutation that splits the set into 2 piles and interleaves them. Its sign is also
, the perfect shuffle is the permutation that splits the set into 2 piles and interleaves them. Its sign is also 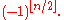
Note that the reverse on n elements and perfect shuffle on 2n elements have the same sign; these are important to the classification of Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s, which are 8-periodic.
Conjugacy classes
The conjugacy classConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es of Sn correspond to the cycle structures of permutations; that is, two elements of Sn are conjugate in Sn if and only if they consist of the same number of disjoint cycles of the same lengths.
For instance, in S5, (1 2 3)(4 5) and (1 4 3)(2 5) are conjugate; (1 2 3)(4 5) and (1 2)(4 5) are not.
A conjugating element of Sn can be constructed in "two line notation" by placing the "cycle notations" of the two conjugate permutations on top of one another. Continuing the previous example:
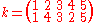
which can be written as the product of cycles, namely:
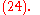
This permutation then relates (1 2 3)(4 5) and (1 4 3)(2 5) via conjugation, i.e.

It is clear that such a permutation is not unique.
Low degree groups
The low-degree symmetric groups have simpler and exceptional structure, and often must be treated separately.Sym(0) and Sym(1): The symmetric groups on the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and the singleton set are trivial, which corresponds to 0! = 1! = 1. In this case the alternating group agrees with the symmetric group, rather than being an index 2 subgroup, and the sign map is trivial.
Sym(2): The symmetric group on two points consists of exactly two elements: the identity and the permutation swapping the two points. It is a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
and so abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. In Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, this corresponds to the fact that the quadratic formula gives a direct solution to the general quadratic polynomial
Quadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
after extracting only a single root. In invariant theory
Invariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
, the representation theory of the symmetric group on two points is quite simple and is seen as writing a function of two variables as a sum of its symmetric and anti-symmetric parts: Setting fs(x,y) = f(x,y) + f(y,x), and fa(x,y) = f(x,y) − f(y,x), one gets that 2·f = fs + fa. This process is known as symmetrization
Symmetrization
In mathematics, symmetrization is a process that converts any function in n variables to a symmetric function in n variables.Conversely, anti-symmetrization converts any function in n variables into an antisymmetric function.-2 variables:...
.
Sym(3): is isomorphic to the dihedral group of order 6
Dihedral group of order 6
The smallest non-abelian group has 6 elements. It is a dihedral group with notation D3 and the symmetric group of degree 3, with notation S3....
, the group of reflection and rotation symmetries of an equilateral triangle, since these symmetries permute the three vertices of the triangle. Cycles of length two correspond to reflections, and cycles of length three are rotations. In Galois theory, the sign map from Sym(3) to Sym(2) corresponds to the resolving quadratic for a cubic polynomial, as discovered by Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
, while the Alt(3) kernel corresponds to the use of the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
of order 3 in the solution, in the form of Lagrange resolvents.
Sym(4): The group S4 is isomorphic to the group of proper rotations about opposite faces, opposite diagonals and opposite edges, 9, 8 and 6 permutations, of the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
. Beyond the group Alt(4), Sym(4) has a Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
V as a proper normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, namely the even transpositions {(1), (12)(34), (13)(24), (14)(23)}, with quotient Sym(3). In Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, this map corresponds to the resolving cubic to a quartic polynomial, which allows the quartic to be solved by radicals, as established by Lodovico Ferrari
Lodovico Ferrari
Lodovico Ferrari was an Italian mathematician.Born in Milan, Italy, grandfather, Bartholomew Ferrari was forced out of Milan to Bologna. He settled in Bologna, Italy and he began his career as the servant of Gerolamo Cardano. He was extremely bright, so Cardano started teaching him mathematics...
. The Klein group can be understood in terms of the Lagrange resolvents of the quartic. The map from Sym(4) to Sym(3) also yields a 2-dimensional irreducible representation, which is an irreducible representation of a symmetric group of degree n of dimension below n−1, which only occurs for n=4.
Sym(5): Sym(5) is the first non-solvable symmetric group. Along with the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,5) and the icosahedral group Alt(5) × Sym(2), Sym(5) is one of the three non-solvable groups of order 120 up to isomorphism. Sym(5) is the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the general quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
, and the fact that Sym(5) is not a solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
translates into the non-existence of a general formula to solve quintic polynomials by radicals. There is an exotic inclusion map
 as a transitive subgroup; the obvious inclusion map
as a transitive subgroup; the obvious inclusion map  fixes a point and thus is not transitive. This yields the outer automorphism of
fixes a point and thus is not transitive. This yields the outer automorphism of 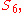 discussed below, and corresponds to the resolvent sextic of a quintic.
discussed below, and corresponds to the resolvent sextic of a quintic.Sym(6): Sym(6), unlike other symmetric groups, has an outer automorphism. Using the language of Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, this can also be understood in terms of Lagrange resolvents. The resolvent of a quintic is of degree 6—this corresponds to an exotic inclusion map
 as a transitive subgroup (the obvious inclusion map
as a transitive subgroup (the obvious inclusion map  fixes a point and thus is not transitive) and, while this map does not make the general quintic solvable, it yields the exotic outer automorphism of
fixes a point and thus is not transitive) and, while this map does not make the general quintic solvable, it yields the exotic outer automorphism of 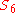 —see automorphisms of the symmetric and alternating groups for details.
—see automorphisms of the symmetric and alternating groups for details.
- Note that while Alt(6) and Alt(7) have an exceptional Schur multiplierSchur multiplierIn mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
(a triple coverCovering groups of the alternating and symmetric groupsIn the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups...
) and that these extend to triple covers of Sym(6) and Sym(7), these do not correspond to exceptional Schur multipliers of the symmetric group.
Maps between symmetric groups
Other than the trivial map and the sign map
and the sign map  the notable maps between symmetric groups, in order of relative dimension
the notable maps between symmetric groups, in order of relative dimensionRelative dimension
In mathematics, specifically linear algebra and geometry, relative dimension is the dual notion to codimension.In linear algebra, given a quotient map V \to Q, the difference dim V − dim Q is the relative dimension; this equals the dimension of the kernel.In fiber bundles, the relative dimension of...
, are:
-
 corresponding to the exceptional normal subgroup
corresponding to the exceptional normal subgroup 
-
 (or rather, a class of such maps up to inner automorphism) corresponding to the outer automorphism of
(or rather, a class of such maps up to inner automorphism) corresponding to the outer automorphism of 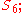
-
 as a transitive subgroup, yielding the outer automorphism of
as a transitive subgroup, yielding the outer automorphism of 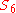 as discussed above.
as discussed above.
Properties
Symmetric groups are Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s and reflection group
Reflection group
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
s. They can be realized as a group of reflections with respect to hyperplanes
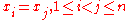 . Braid group
. Braid groupBraid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s Bn admit symmetric groups Sn as quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
s.
Cayley's theorem
Cayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
states that every group G is isomorphic to a subgroup of the symmetric group on the elements of G, as a group acts on itself faithfully by (left or right) multiplication.
Relation with alternating group
For n≥5, the alternating group An is simpleSimple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, and the induced quotient is the sign map:
 which is split by taking a transposition of two elements. Thus Sn is the semidirect product
which is split by taking a transposition of two elements. Thus Sn is the semidirect product  and has no other proper normal subgroups, as they would intersect An in either the identity (and thus themselves be the identity or a 2-element group, which is not normal), or in An (and thus themselves be An or Sn).
and has no other proper normal subgroups, as they would intersect An in either the identity (and thus themselves be the identity or a 2-element group, which is not normal), or in An (and thus themselves be An or Sn).Sn acts on its subgroup An by conjugation, and for n ≠ 6, Sn is the full automorphism group of
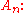
 Conjugation by even elements are inner automorphism
Conjugation by even elements are inner automorphismInner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
s of An while the outer automorphism of An of order 2 corresponds to conjugation by an odd element. For n = 6, there is an exceptional outer automorphism of An so Sn is not the full automorphism group of An.
Conversely, for n ≠ 6, Sn has no outer automorphisms, and for n ≠ 2 it has no center, so for n ≠ 2, 6 it is a complete group
Complete group
In mathematics, a group G is said to be complete if every automorphism of G is inner, and the group is a centerless group; that is, it has a trivial outer automorphism group and trivial center....
, as discussed in automorphism group, below.
For n ≥ 5, Sn is an almost simple group
Almost simple group
In mathematics, a group is said to be almost simple if it contains a non-abelian simple group and is contained within the automorphism group of that simple group: if it fits between a simple group and its automorphism group.More precisely, a group is almost simple if it is isomorphic to such a group...
, as it lies between the simple group An and its group of automorphisms.
Generators and relations
The symmetric group on n-letters, Sn, may be described as follows. It has generators: and relations:
and relations:
One thinks of
 as swapping the i-th and i+1-st position.
as swapping the i-th and i+1-st position.Other popular generating sets include the set of transpositions that swap 1 and i for 2 ≤ i ≤ n and any set containing an n-cycle and a 2-cycle.
Normal subgroups
The normal subgroupNormal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s of the finite symmetric groups are well understood. If n ≤ 2, Sn has at most 2 elements, and so has no nontrivial proper subgroups. The alternating group of degree n is always a normal subgroup, a proper one for n ≥ 2 and nontrivial for n ≥ 3; for n ≥ 3 it is in fact the only non-identity proper normal subgroup of Sn, except when n = 4 where there is one additional such normal subgroup, which is isomorphic to the Klein four group.
The symmetric group on an infinite set does not have an associated alternating group: not all elements can be written as a (finite) product of transpositions. However it does contain a normal subgroup S of permutations that fix all but finitely many elements, and such permutations can be classified as either even or odd. The even elements of S form the alternating subgroup A of S, and since A is even a characteristic subgroup
Characteristic subgroup
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
of S, it is also a normal subgroup of the full symmetric group of the infinite set. The groups A and S are the only non-identity proper normal subgroups of the symmetric group on a countably infinite set. For more details see or .
Maximal subgroups
The maximal subgroupMaximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
s of the finite symmetric groups fall into three classes: the intransitive, the imprimitive, and the primitive. The intransitive maximal subgroups are exactly those of the form Sym(k) × Sym(n−k) for 1 ≤ k < n/2. The imprimitive maximal subgroups are exactly those of the form Sym(k) wr Sym( n/k ) where 2 ≤ k ≤ n/2 is a proper divisor of n and "wr" denotes the wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
acting imprimitively. The primitive maximal subgroups are more difficult to identify, but with the assistance of the O'Nan–Scott theorem and the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, gave a fairly satisfactory description of the maximal subgroups of this type according to .
Sylow subgroups
The Sylow subgroups of the symmetric groups are important examples of p-groupsP-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
. They are more easily described in special cases first:
The Sylow p-subgroups of the symmetric group of degree p are just the cyclic subgroups generated by p-cycles. There are (p − 1)!/(p − 1) = (p − 2)! such subgroups simply by counting generators. The normalizer therefore has order p·(p − 1) and is known as a Frobenius group
Frobenius group
In mathematics, a Frobenius group is a transitive permutation group on a finite set, such that no non-trivial elementfixes more than one point and some non-trivial element fixes a point.They are named after F. G. Frobenius.- Structure :...
Fp(p − 1) (especially for p = 5), and as the affine general linear group, AGL(1, p).
The Sylow p-subgroups of the symmetric group of degree p2 are the wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
of two cyclic groups of order p. For instance, when p = 3, a Sylow 3-subgroup of Sym(9) is generated by a = (1, 4, 7)(2, 5, 8)(3, 6, 9) and the elements x = (1,2,3), y = (4, 5, 6), z = (7, 8, 9), and every element of the Sylow 3-subgroup has the form aixjykzl for 0 ≤ i,j,k,l ≤ 2.
The Sylow p-subgroups of the symmetric group of degree pn are sometimes denoted Wp(n), and using this notation one has that Wp(n + 1) is the wreath product of Wp(n) and Wp(1).
In general, the Sylow p-subgroups of the symmetric group of degree n are a direct product of ai copies of Wp(i), where 0 ≤ ai ≤ p − 1 and n = a0 + p·a1 + ... + pk·ak.
For instance, W2(1) = C2 and W2(2) = D8, the dihedral group of order 8, and so a Sylow 2-subgroup of the symmetric group of degree 7 is generated by { (1,3)(2,4), (1,2), (3,4), (5,6) } and is isomorphic to D8 × C2.
These calculations are attributed to and described in more detail in . Note however that attributes the result to an 1844 work of Cauchy, and mentions that it is even covered in textbook form in .
Transitive subgroups
A transitive subgroup of Sn is a subgroup whose action on {1, 2, ,..., n} is transitive. For example, the Galois group of a (finite) Galois extensionGalois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
is a transitive subgroup of Sn, for some n.
Automorphism group
| n | 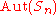 |
 |
 |
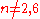 |
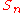 |
1 | 1 |
 |
1 | 1 | 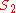 |
 |
 |
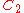 |
1 |
For
 ,
,  is a complete group
is a complete groupComplete group
In mathematics, a group G is said to be complete if every automorphism of G is inner, and the group is a centerless group; that is, it has a trivial outer automorphism group and trivial center....
: its center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
and outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
are both trivial.
For n = 2, the automorphism group is trivial, but
 is not trivial: it is isomorphic to
is not trivial: it is isomorphic to 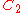 , which is abelian, and hence the center is the whole group.
, which is abelian, and hence the center is the whole group.For n = 6, it has an outer automorphism of order 2:
 , and the automorphism group is a semidirect product
, and the automorphism group is a semidirect product
In fact, for any set X of cardinality other than 6, every automorphism of the symmetric group on X is inner, a result first due to according to .
Homology
The group homology of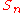 is quite regular and stabilizes: the first homology (concretely, the abelianization) is:
is quite regular and stabilizes: the first homology (concretely, the abelianization) is:
The first homology group is the abelianization, and corresponds to the sign map
 which is the abelianization for n ≥ 2; for n < 2 the symmetric group is trivial. This homology is easily computed as follows: Sn is generated by involutions (2-cycles, which have order 2), so the only non-trivial maps
which is the abelianization for n ≥ 2; for n < 2 the symmetric group is trivial. This homology is easily computed as follows: Sn is generated by involutions (2-cycles, which have order 2), so the only non-trivial maps  are to
are to  and all involutions are conjugate, hence map to the same element in the abelianization (since conjugation is trivial in abelian groups). Thus the only possible maps
and all involutions are conjugate, hence map to the same element in the abelianization (since conjugation is trivial in abelian groups). Thus the only possible maps  send an involution to 1 (the trivial map) or to −1 (the sign map). One must also show that the sign map is well-defined, but assuming that, this gives the first homology of Sn.
send an involution to 1 (the trivial map) or to −1 (the sign map). One must also show that the sign map is well-defined, but assuming that, this gives the first homology of Sn.The second homology (concretely, the Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
) is:

This was computed in , and corresponds to the double cover of the symmetric group
Covering groups of the alternating and symmetric groups
In the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups...
, 2 · Sn.
Note that the exceptional
Exceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
low-dimensional homology of the alternating group (
 corresponding to non-trivial abelianization, and
corresponding to non-trivial abelianization, and  due to the exceptional 3-fold cover) does not change the homology of the symmetric group; the alternating group phenomena do yield symmetric group phenomena – the map
due to the exceptional 3-fold cover) does not change the homology of the symmetric group; the alternating group phenomena do yield symmetric group phenomena – the map  extends to
extends to  and the triple covers of
and the triple covers of 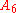 and
and  extend to triple covers of
extend to triple covers of 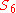 and
and  – but these are not homological – the map
– but these are not homological – the map  does not change the abelianization of
does not change the abelianization of  and the triple covers do not correspond to homology either.
and the triple covers do not correspond to homology either.The homology "stabilizes" in the sense of stable homotopy theory: there is an inclusion map
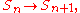 and for fixed k, the induced map on homology
and for fixed k, the induced map on homology 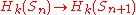 is an isomorphism for sufficiently high n. This is analogous to the homology of families Lie groups stabilizing.
is an isomorphism for sufficiently high n. This is analogous to the homology of families Lie groups stabilizing.The homology of the infinite symmetric group is computed in , with the cohomology algebra forming a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
.
Representation theory
The representation theory of the symmetric groupRepresentation theory of the symmetric group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to problems of quantum...
is a particular case of the representation theory of finite groups
Representation theory of finite groups
In mathematics, representation theory is a technique for analyzing abstract groups in terms of groups of linear transformations. See the article on group representations for an introduction...
, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
theory to problems of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
for a number of identical particles
Identical particles
Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...
.
The symmetric group Sn has order n
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es are labeled by partitions of n. Therefore according to the representation theory of a finite group, the number of inequivalent irreducible representations, over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, is equal to the number of partitions of n. Unlike the general situation for finite groups, there is in fact a natural way to parametrize irreducible representation by the same set that parametrizes conjugacy classes, namely by partitions of n or equivalently Young diagrams of size n.
Each such irreducible representation can be realized over the integers (every permutation acting by a matrix with integer coefficients); it can be explicitly constructed by computing the Young symmetrizer
Young symmetrizer
In mathematics, a Young symmetrizer is an element of the group algebra of the symmetric group, constructed in such a way that the image of the element corresponds to an irreducible representation of the symmetric group over the complex numbers. A similar construction works over any field, and the...
s acting on a space generated by the Young tableau
Young tableau
In mathematics, a Young tableau is a combinatorial object useful in representation theory. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at...
x of shape given by the Young diagram.
Over other field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s the situation can become much more complicated. If the field K has characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
equal to zero or greater than n then by Maschke's theorem
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
KSn is semisimple. In these cases the irreducible representations defined over the integers give the complete set of irreducible representations (after reduction modulo the characteristic if necessary).
However, the irreducible representations of the symmetric group are not known in arbitrary characteristic. In this context it is more usual to use the language of module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s rather than representations. The representation obtained from an irreducible representation defined over the integers by reducing modulo the characteristic will not in general be irreducible. The modules so constructed are called Specht modules, and every irreducible does arise inside some such module. There are now fewer irreducibles, and although they can be classified they are very poorly understood. For example, even their dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
s are not known in general.
The determination of the irreducible modules for the symmetric group over an arbitrary field is widely regarded as one of the most important open problems in representation theory.
See also
- History of group theoryHistory of group theoryThe history of group theory, a mathematical domain studying groups in their various forms, has evolved in various parallel threads. There are three historical roots of group theory: the theory of algebraic equations, number theory and geometry...
- Symmetric inverse semigroup
- Signed symmetric group
- Generalized symmetric groupGeneralized symmetric groupIn mathematics, the generalized symmetric group is the wreath product S := Z_m \wr S_n of the cyclic group of order m and the symmetric group on n letters.- Examples :...
External links
- Marcus du Sautoy: Symmetry, reality's riddle (video of a talk)