
Erlangen program
Encyclopedia
An influential research program and manifesto was published in 1872 by Felix Klein
, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen. This Erlangen Program (Erlanger Programm) — Klein was then at Erlangen
— proposed a new solution to the problem how to classify and characterize geometries
on the basis of projective geometry
and group theory
.
At that time, a family of new non-Euclidean geometries
had already emerged, without adequate clarifications of their mutual hierarchy and relationships. What Klein suggested was fundamentally innovative in three ways:
Ultimately Élie Cartan
generalized Klein's homogeneous model spaces to (Cartan) connections on certain principal bundles, placing the problem in the framework of Riemannian geometry
.
, geometry had meant the geometry of Euclidean space
of two dimensions (plane geometry) or of three dimensions (solid geometry
). In the first half of the nineteenth century there had been several developments complicating the picture. Mathematical applications required geometry of four or more dimensions; the close scrutiny of the foundations of the traditional Euclidean geometry had revealed the independence of the parallel postulate
from the others, and non-Euclidean geometry
had been born. Klein proposed an idea that all these new geometries are just special cases of the projective geometry
, as already developed by Poncelet
, Möbius
, Cayley
and others. Klein also strongly suggested to mathematical physicists that even a moderate cultivation of the projective purview might bring substantial benefits to them.
With every geometry, Klein associated an underlying group of symmetries
. The hierarchy of geometries is thus mathematically represented as a hierarchy of these groups
, and hierarchy of their invariants
. For example, lengths, angles and areas are preserved with respect to the Euclidean group
of symmetries, while only the incidence structure
and the cross-ratio
are preserved under the most general projective transformations
. A concept of parallelism
, which is preserved in affine geometry
, is not meaningful in projective geometry
. Then, by abstracting the underlying groups
of symmetries from the geometries, the relationships between them can be re-established at the group level. Since the group of affine geometry is a subgroup
of the group of projective geometry, any notion invariant in projective geometry is a priori meaningful in affine geometry; but not the other way round. If you add required symmetries, you have a more powerful theory but fewer concepts and theorems (which will be deeper and more general).
s; but not for a uniquely determined group. Changing the group changes the appropriate geometric language.
In today's language, the groups concerned in classical geometry are all very well known as Lie group
s: the classical groups. The specific relationships are quite simply described, using technical language.
in n dimensions is the symmetry group of n-dimensional projective space
(the general linear group
of degree n + 1, quotiented by scalar matrices). The affine group
will be the subgroup respecting (mapping to itself, not fixing pointwise) the chosen hyperplane at infinity. This subgroup has a known structure (semidirect product
of the general linear group
of degree n with the subgroup of translation
s). This description then tells us which properties are 'affine'. In Euclidean plane geometry terms, being a parallelogram is affine since affine transformations always take one parallelogram to another one. Being a circle is not affine since an affine shear will take a circle into an ellipse.
To explain accurately the relationship between affine and Euclidean geometry, we now need to pin down the group of Euclidean geometry within the affine group. The Euclidean group
is in fact (using the previous description of the affine group) the semi-direct product of the orthogonal (rotation and reflection) group with the translations.
, for example); and the idea of transformations and of synthesis using groups of symmetry is of course now standard too in physics
.
When topology
is routinely described in terms of properties invariant
under homeomorphism
, one can see the underlying idea in operation. The groups involved will be infinite-dimensional in almost all cases – and not Lie group
s – but the philosophy is the same. Of course this mostly speaks to the pedagogical influence of Klein. Books such as those by H.S.M. Coxeter routinely used the Erlangen program approach to help 'place' geometries. In pedagogic terms, the program became transformation geometry
, a mixed blessing in the sense that it builds on stronger intuitions than the style of Euclid
, but is less easily converted into a logical system.
In his book Structuralism (1970) Jean Piaget
says, "In the eyes of contemporary structuralist mathematicians, like Bourbaki, the Erlangen Program amounts to only a partial victory for structuralism, since they want to subordinate all mathematics, not just geometry, to the idea of structure
."
For a geometry and its group, an element of the group is sometimes called a motion of the geometry. For example, one can learn about the Poincaré half-plane model
of hyperbolic geometry
through a development based on hyperbolic motion
s. Such a development enables one to methodically prove the ultraparallel theorem
by successive motions.
The Erlangen Program is carried into mathematical logic by Alfred Tarski
in his analysis of propositional truth.
with isomorphic automorphism groups. There arises the question of reading the Erlangen program from the abstract group, to the geometry.
One example: oriented (i.e., reflections
not included) elliptic geometry
(i.e., the surface of an n-sphere with opposite points identified) and oriented spherical geometry
(the same non-Euclidean geometry, but with opposite points not identified) have isomorphic automorphism group, SO(n+1) for even n. These may appear to be distinct. It turns out, however, that the geometries are very closely related, in a way that can be made precise.
To take another example, elliptic geometries
with different radii of curvature
have isomorphic automorphism groups. That does not really count as a critique as all such geometries are isomorphic. General Riemannian geometry
falls outside the boundaries of the program.
Some further notable examples have come up in physics.
Firstly, n-dimensional hyperbolic geometry
, n-dimensional de Sitter space
and (n−1)-dimensional inversive geometry all have isomorphic automorphism groups,
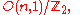
the orthochronous Lorentz group
, for n ≥ 3. But these are apparently distinct geometries. Here some interesting results enter, from the physics. It has been shown that physics models in each of the three geometries are "dual" for some models.
Again, n-dimensional anti de Sitter space
and (n−1)-dimensional conformal space with "Lorentzian" signature (in contrast with conformal space with "Euclidean" signature, which is identical to inversive geometry, for three dimensions or greater) have isomorphic automorphism groups, but are distinct geometries. Once again, there are models in physics with "dualities" between both spaces
. See AdS/CFT for more details.
The covering group of SU(2,2) is isomorphic to the covering group of SO(4,2), which is the symmetry group of a 4D conformal Minkowski space and a 5D anti de Sitter space and a complex four-dimensional twistor space.
The Erlangen program can therefore still be considered fertile, in relation with dualities in physics.
Relations of the Erlangen program with work of C. Ehresmann on groupoids in geometry is considered in the article below by Pradines.
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen. This Erlangen Program (Erlanger Programm) — Klein was then at Erlangen
Erlangen
Erlangen is a Middle Franconian city in Bavaria, Germany. It is located at the confluence of the river Regnitz and its large tributary, the Untere Schwabach.Erlangen has more than 100,000 inhabitants....
— proposed a new solution to the problem how to classify and characterize geometries
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
on the basis of projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
and group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
.
At that time, a family of new non-Euclidean geometries
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
had already emerged, without adequate clarifications of their mutual hierarchy and relationships. What Klein suggested was fundamentally innovative in three ways:
- projective geometry was emphasized as the unifying frame for all other geometries considered by him. In particular, the affineAffine spaceIn mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, metricMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, and EuclideanEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
geometries are just special and gradually more restrictive cases of projective geometry.
- Klein proposed that group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a branch of mathematics that uses algebraic methods to abstract the idea of symmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, was the most useful way of organizing geometrical knowledge; at the time it had already been introduced into the theory of equationsTheory of equationsIn mathematics, the theory of equations comprises a major part of traditional algebra. Topics include polynomials, algebraic equations, separation of roots including Sturm's theorem, approximation of roots, and the application of matrices and determinants to the solving of equations.From the point...
in the form of Galois theoryGalois theoryIn mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
.
- Klein made much more explicit the idea that each geometrical language had its own, appropriate concepts, so that for example projective geometry rightly talked about conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s, but not about circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s or angleAngleIn geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s because those notions were not invariant under projective transformations (something familiar in geometrical perspective). The way the multiple languages of geometry then came back together could be explained by the way subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of a symmetry groupSymmetry groupThe symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
related to each other.
Ultimately Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
generalized Klein's homogeneous model spaces to (Cartan) connections on certain principal bundles, placing the problem in the framework of Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
.
The problems of nineteenth century geometry
Is there one 'geometry' or many? Since EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, geometry had meant the geometry of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of two dimensions (plane geometry) or of three dimensions (solid geometry
Solid geometry
In mathematics, solid geometry was the traditional name for the geometry of three-dimensional Euclidean space — for practical purposes the kind of space we live in. It was developed following the development of plane geometry...
). In the first half of the nineteenth century there had been several developments complicating the picture. Mathematical applications required geometry of four or more dimensions; the close scrutiny of the foundations of the traditional Euclidean geometry had revealed the independence of the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
from the others, and non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
had been born. Klein proposed an idea that all these new geometries are just special cases of the projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, as already developed by Poncelet
Jean-Victor Poncelet
Jean-Victor Poncelet was a French engineer and mathematician who served most notably as the commandant general of the École Polytechnique...
, Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
, Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
and others. Klein also strongly suggested to mathematical physicists that even a moderate cultivation of the projective purview might bring substantial benefits to them.
With every geometry, Klein associated an underlying group of symmetries
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
. The hierarchy of geometries is thus mathematically represented as a hierarchy of these groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, and hierarchy of their invariants
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
. For example, lengths, angles and areas are preserved with respect to the Euclidean group
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
of symmetries, while only the incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
and the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
are preserved under the most general projective transformations
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
. A concept of parallelism
Parallelism
Parallelism may refer to:* Angle of parallelism, the angle at one vertex of a right hyperbolic triangle that has two hyperparallel sides* Conscious parallelism, price-fixing between competitors in an oligopoly that occurs without an actual spoken agreement between the parties* Parallel computing,...
, which is preserved in affine geometry
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
, is not meaningful in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
. Then, by abstracting the underlying groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of symmetries from the geometries, the relationships between them can be re-established at the group level. Since the group of affine geometry is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the group of projective geometry, any notion invariant in projective geometry is a priori meaningful in affine geometry; but not the other way round. If you add required symmetries, you have a more powerful theory but fewer concepts and theorems (which will be deeper and more general).
Homogeneous spaces
In other words, the "traditional spaces" are homogeneous spaceHomogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
s; but not for a uniquely determined group. Changing the group changes the appropriate geometric language.
In today's language, the groups concerned in classical geometry are all very well known as Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s: the classical groups. The specific relationships are quite simply described, using technical language.
Examples
For example the group of projective geometryProjective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
in n dimensions is the symmetry group of n-dimensional projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
(the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of degree n + 1, quotiented by scalar matrices). The affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
will be the subgroup respecting (mapping to itself, not fixing pointwise) the chosen hyperplane at infinity. This subgroup has a known structure (semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of degree n with the subgroup of translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s). This description then tells us which properties are 'affine'. In Euclidean plane geometry terms, being a parallelogram is affine since affine transformations always take one parallelogram to another one. Being a circle is not affine since an affine shear will take a circle into an ellipse.
To explain accurately the relationship between affine and Euclidean geometry, we now need to pin down the group of Euclidean geometry within the affine group. The Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
is in fact (using the previous description of the affine group) the semi-direct product of the orthogonal (rotation and reflection) group with the translations.
| Geometric Group | Number of copies of orthogonal group (rotations and reflections) | Number of copies of additive group (translations) | Number of copies of multiplicative group (dilations) |
|---|---|---|---|
| 2-D Euclidean | 1 | 2 | 0 |
| 2-D Hyperbolic | 1 | 1 | 1 |
| Elliptic | |||
| Affine | |||
| Projective |
Influence on later work
The long-term effects of the Erlangen program can be seen all over pure mathematics (see tacit use at congruence (geometry)Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
, for example); and the idea of transformations and of synthesis using groups of symmetry is of course now standard too in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
.
When topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
is routinely described in terms of properties invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
, one can see the underlying idea in operation. The groups involved will be infinite-dimensional in almost all cases – and not Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s – but the philosophy is the same. Of course this mostly speaks to the pedagogical influence of Klein. Books such as those by H.S.M. Coxeter routinely used the Erlangen program approach to help 'place' geometries. In pedagogic terms, the program became transformation geometry
Transformation geometry
In mathematics, transformation geometry is a name for a pedagogic theory for teaching Euclidean geometry, based on the Erlangen programme. Felix Klein, who pioneered this point of view, was himself interested in mathematical education. It took many years, though, for his "modern" point of view to...
, a mixed blessing in the sense that it builds on stronger intuitions than the style of Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, but is less easily converted into a logical system.
In his book Structuralism (1970) Jean Piaget
Jean Piaget
Jean Piaget was a French-speaking Swiss developmental psychologist and philosopher known for his epistemological studies with children. His theory of cognitive development and epistemological view are together called "genetic epistemology"....
says, "In the eyes of contemporary structuralist mathematicians, like Bourbaki, the Erlangen Program amounts to only a partial victory for structuralism, since they want to subordinate all mathematics, not just geometry, to the idea of structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
."
For a geometry and its group, an element of the group is sometimes called a motion of the geometry. For example, one can learn about the Poincaré half-plane model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
through a development based on hyperbolic motion
Hyperbolic motion
In geometry, hyperbolic motions are isometric automorphisms of a hyperbolic space. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein in his Erlangen program...
s. Such a development enables one to methodically prove the ultraparallel theorem
Ultraparallel theorem
In hyperbolic geometry, the ultraparallel theorem states that every pair of ultraparallel lines in the hyperbolic plane has a unique common perpendicular hyperbolic line.-Proof in the Poincaré half-plane model:Leta...
by successive motions.
The Erlangen Program is carried into mathematical logic by Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
in his analysis of propositional truth.
Abstract returns from the Erlangen program
Quite often, it appears there are two or more distinct geometriesGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
with isomorphic automorphism groups. There arises the question of reading the Erlangen program from the abstract group, to the geometry.
One example: oriented (i.e., reflections
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
not included) elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
(i.e., the surface of an n-sphere with opposite points identified) and oriented spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
(the same non-Euclidean geometry, but with opposite points not identified) have isomorphic automorphism group, SO(n+1) for even n. These may appear to be distinct. It turns out, however, that the geometries are very closely related, in a way that can be made precise.
To take another example, elliptic geometries
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
with different radii of curvature
Radius of curvature (mathematics)
In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise...
have isomorphic automorphism groups. That does not really count as a critique as all such geometries are isomorphic. General Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
falls outside the boundaries of the program.
Some further notable examples have come up in physics.
Firstly, n-dimensional hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, n-dimensional de Sitter space
De Sitter space
In mathematics and physics, a de Sitter space is the analog in Minkowski space, or spacetime, of a sphere in ordinary, Euclidean space. The n-dimensional de Sitter space , denoted dS_n, is the Lorentzian manifold analog of an n-sphere ; it is maximally symmetric, has constant positive curvature,...
and (n−1)-dimensional inversive geometry all have isomorphic automorphism groups,
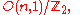
the orthochronous Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, for n ≥ 3. But these are apparently distinct geometries. Here some interesting results enter, from the physics. It has been shown that physics models in each of the three geometries are "dual" for some models.
Again, n-dimensional anti de Sitter space
Anti de Sitter space
In mathematics and physics, n-dimensional anti de Sitter space, sometimes written AdS_n, is a maximally symmetric Lorentzian manifold with constant negative scalar curvature...
and (n−1)-dimensional conformal space with "Lorentzian" signature (in contrast with conformal space with "Euclidean" signature, which is identical to inversive geometry, for three dimensions or greater) have isomorphic automorphism groups, but are distinct geometries. Once again, there are models in physics with "dualities" between both spaces
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. See AdS/CFT for more details.
The covering group of SU(2,2) is isomorphic to the covering group of SO(4,2), which is the symmetry group of a 4D conformal Minkowski space and a 5D anti de Sitter space and a complex four-dimensional twistor space.
The Erlangen program can therefore still be considered fertile, in relation with dualities in physics.
Relations of the Erlangen program with work of C. Ehresmann on groupoids in geometry is considered in the article below by Pradines.

