
Average
Encyclopedia
In mathematics
, an average, or central tendency of a data set
is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average.
There are many different descriptive statistics
that can be chosen as a measurement of the central tendency of the data items. These include arithmetic mean
, the median
and the mode
. Other statistical measures such as the standard deviation
and the range
are called measures of spread and describe how spread out the data is.
An average is a single value that is meant to typify a list of values. If all the numbers in the list are the same, then this number should be used. If the numbers are not the same, the average is calculated by combining the values from the set in a specific way and computing a single number as being the average of the set.
The most common method is the arithmetic mean
but there are many other types of central tendency, such as median
(which is used most often when the distribution
of the values is skewed
with some small numbers of very high values, as seen with house prices or incomes).
-- the arithmetic mean, the geometric mean, and the harmonic mean.
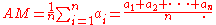
The arithmetic mean, often simply called the mean, of two numbers, such as 2 and 8, is obtained by finding a value A such that 2 + 8 = A + A. One may find that A = (2 + 8)/2 = 5. Switching the order of 2 and 8 to read 8 and 2 does not change the resulting value obtained for A. The mean 5 is not less than the minimum 2 nor greater than the maximum 8. If we increase the number of terms in the list for which we want an average, we get, for example, that the arithmetic mean of 2, 8, and 11 is found by solving for the value of A in the equation 2 + 8 + 11 = A + A + A. One finds that A = (2 + 8 + 11)/3 = 7.
Geometric mean can be thought of as the antilog of the arithmetic mean of the logs
of the numbers.
Example: Geometric mean of 2 and 8 is
One example where it is useful is calculating the average speed for a number of fixed-distance trips. For example, if the speed for going from point A to B was 60 km/h, and the speed for returning from B to A was 40 km/h, then the average speed is given by
It is easy to remember noting that the alphabetical order of the letters A, G, and H is preserved in the inequality. See Inequality of arithmetic and geometric means
.
The mode has the advantage that it can be used with non-numerical data (e.g., red cars are most frequent), while other averages cannot.
The median is the middle number of the group when they are ranked in order. (If there are an even number of numbers, the mean of the middle two is taken.)
Thus to find the median, order the list according to its elements' magnitude and then repeatedly remove the pair consisting of the highest and lowest values until either one or two values are left. If exactly one value is left, it is the median; if two values, the median is the arithmetic mean of these two. This method takes the list 1, 7, 3, 13 and orders it to read 1, 3, 7, 13. Then the 1 and 13 are removed to obtain the list 3, 7. Since there are two elements in this remaining list, the median is their arithmetic mean, (3 + 7)/2 = 5.
This method can be generalized to examples in which the periods are not all of one-year duration. Average percentage of a set of returns is a variation on the geometric average that provides the intensive property of a return per year corresponding to a list of percentage returns. For example, consider a period of a half of a year for which the return is −23% and a period of two and one half years for which the return is +13%. The average percentage return for the combined period is the single year return, R, that is the solution of the following equation: , giving an average percentage return R of 0.0600 or 6.00%.
explains the symbols used below.
, namely minimizing variation from the center. That is, given a measure of statistical dispersion
, one asks for a measure of central tendency that minimizes variation: such that variation from the center is minimal among all choices of center. In a quip, "dispersion precedes location". In the sense of Lp spaces
, the correspondence is:
Thus standard deviation about the mean is lower than standard deviation about any other point, and the maximum deviation about the midrange is lower than the maximum deviation about any other point. The uniqueness of this characterization of mean follows from convex optimization. Indeed, for a given (fixed) data set x, the function

represents the dispersion about a constant value c relative to the L2 norm. Because the function ƒ2 is a strictly convex
coercive function
, the minimizer exists and is unique.
Note that the median in this sense is not in general unique, and in fact any point between the two central points of a discrete distribution minimizes average absolute deviation. The dispersion in the L1 norm, given by
is not strictly convex, whereas strict convexity is needed to ensure uniqueness of the minimizer. In spite of this, the minimizer is unique for the L∞ norm.
, trimedian, and normalized mean, with their generalizations.
One can create one's own average metric using generalized f-mean:
where f is any invertible function. The harmonic mean is an example of this using f(x) = 1/x, and the geometric mean is another, using f(x) = log x. Another example, expmean (exponential mean) is a mean using the function f(x) = ex, and it is inherently biased towards the higher values. However, this method for generating means is not general enough to capture all averages. A more general method for defining an average, y, takes any function of a list g(x1, x2, ..., xn), which is symmetric under permutation of the members of the list, and equates it to the same function with the value of the average replacing each member of the list: g(x1, x2, ..., xn) = g(y, y, ..., y). This most general definition still captures the important property of all averages that the average of a list of identical elements is that element itself.
The function g(x1, x2, ..., xn) =x1+x2+ ...+ xn provides the arithmetic mean.
The function g(x1, x2, ..., xn) =x1·x2· ...· xn provides the geometric mean.
The function g(x1, x2, ..., xn) =x1−1+x2−1+ ...+ xn−1 provides the harmonic mean. (See John Bibby (1974) “Axiomatisations of the average and a further generalisation of monotonic sequences,” Glasgow Mathematical Journal, vol. 15, pp. 63–65.)

, the average value of an integrable
function ƒ on an interval [a,b] is defined by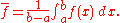
Marine damage is either particular average, which is borne only by the owner of the damaged property, or general average
, where the owner can claim a proportional contribution from all the parties to the marine venture. The type of calculations used in adjusting general average gave rise to the use of "average" to mean "arithmetic mean".
However, according to the Oxford English Dictionary, the earliest usage in English (1489 or earlier) appears to be an old legal term for a tenant's day labour obligation to a sheriff, probably anglicised from "avera" found in the English Domesday Book
(1085). This pre-existing term thus lay to hand when an equivalent for avarie was wanted.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an average, or central tendency of a data set
Data set
A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...
is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average.
There are many different descriptive statistics
Descriptive statistics
Descriptive statistics quantitatively describe the main features of a collection of data. Descriptive statistics are distinguished from inferential statistics , in that descriptive statistics aim to summarize a data set, rather than use the data to learn about the population that the data are...
that can be chosen as a measurement of the central tendency of the data items. These include arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
, the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
and the mode
Mode (statistics)
In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
. Other statistical measures such as the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
and the range
Range (statistics)
In the descriptive statistics, the range is the length of the smallest interval which contains all the data. It is calculated by subtracting the smallest observation from the greatest and provides an indication of statistical dispersion.It is measured in the same units as the data...
are called measures of spread and describe how spread out the data is.
An average is a single value that is meant to typify a list of values. If all the numbers in the list are the same, then this number should be used. If the numbers are not the same, the average is calculated by combining the values from the set in a specific way and computing a single number as being the average of the set.
The most common method is the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
but there are many other types of central tendency, such as median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
(which is used most often when the distribution
Frequency distribution
In statistics, a frequency distribution is an arrangement of the values that one or more variables take in a sample. Each entry in the table contains the frequency or count of the occurrences of values within a particular group or interval, and in this way, the table summarizes the distribution of...
of the values is skewed
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
with some small numbers of very high values, as seen with house prices or incomes).
Calculation
The three most common averages are the Pythagorean meansPythagorean means
In mathematics, the three classical Pythagorean means are the arithmetic mean , the geometric mean , and the harmonic mean...
-- the arithmetic mean, the geometric mean, and the harmonic mean.
Arithmetic mean
If n numbers are given, each number denoted by ai, where i = 1, ..., n, the arithmetic mean is the [sum] of the ai's divided by n or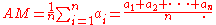
The arithmetic mean, often simply called the mean, of two numbers, such as 2 and 8, is obtained by finding a value A such that 2 + 8 = A + A. One may find that A = (2 + 8)/2 = 5. Switching the order of 2 and 8 to read 8 and 2 does not change the resulting value obtained for A. The mean 5 is not less than the minimum 2 nor greater than the maximum 8. If we increase the number of terms in the list for which we want an average, we get, for example, that the arithmetic mean of 2, 8, and 11 is found by solving for the value of A in the equation 2 + 8 + 11 = A + A + A. One finds that A = (2 + 8 + 11)/3 = 7.
Geometric mean
The geometric mean of n numbers is obtained by multiplying them all together and then taking the nth root. In algebraic terms, the geometric mean of a1, a2, ..., an is defined asGeometric mean can be thought of as the antilog of the arithmetic mean of the logs
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the numbers.
Example: Geometric mean of 2 and 8 is

Harmonic mean
Harmonic mean for a set of numbers a1, a2, ..., an is defined as the reciprocal of the arithmetic mean of the reciprocals of ai's:One example where it is useful is calculating the average speed for a number of fixed-distance trips. For example, if the speed for going from point A to B was 60 km/h, and the speed for returning from B to A was 40 km/h, then the average speed is given by
Inequality concerning AM, GM, and HM
A well known inequality concerning arithmetic, geometric, and harmonic means for any set of positive numbers isIt is easy to remember noting that the alphabetical order of the letters A, G, and H is preserved in the inequality. See Inequality of arithmetic and geometric means
Inequality of arithmetic and geometric means
In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...
.
Mode and median
The most frequently occurring number in a list is called the mode. The mode of the list (1, 2, 2, 3, 3, 3, 4) is 3. The mode is not necessarily well defined, the list (1, 2, 2, 3, 3, 5) has the two modes 2 and 3. The mode can be subsumed under the general method of defining averages by understanding it as taking the list and setting each member of the list equal to the most common value in the list if there is a most common value. This list is then equated to the resulting list with all values replaced by the same value. Since they are already all the same, this does not require any change. The mode is more meaningful and potentially useful if there are many numbers in the list, and the frequency of the numbers progresses smoothly (e.g., if out of a group of 1000 people, 30 people weigh 61 kg, 32 weigh 62 kg, 29 weigh 63 kg, and all the other possible weights occur less frequently, then 62 kg is the mode).The mode has the advantage that it can be used with non-numerical data (e.g., red cars are most frequent), while other averages cannot.
The median is the middle number of the group when they are ranked in order. (If there are an even number of numbers, the mean of the middle two is taken.)
Thus to find the median, order the list according to its elements' magnitude and then repeatedly remove the pair consisting of the highest and lowest values until either one or two values are left. If exactly one value is left, it is the median; if two values, the median is the arithmetic mean of these two. This method takes the list 1, 7, 3, 13 and orders it to read 1, 3, 7, 13. Then the 1 and 13 are removed to obtain the list 3, 7. Since there are two elements in this remaining list, the median is their arithmetic mean, (3 + 7)/2 = 5.
Average Percentage Return
The average percentage return is a type of average used in finance. It is an example of a geometric mean. For example, if we are considering a period of two years, and the investment return in the first year is −10% and the return in the second year is +60%, then the average percentage return, R, can be obtained by solving the equation: . The value of R that makes this equation true is 0.2, or 20%. Note that changing the order to find the average percentage returns of +60% and −10% gives the same result as the average percentage returns of −10% and +60%.This method can be generalized to examples in which the periods are not all of one-year duration. Average percentage of a set of returns is a variation on the geometric average that provides the intensive property of a return per year corresponding to a list of percentage returns. For example, consider a period of a half of a year for which the return is −23% and a period of two and one half years for which the return is +13%. The average percentage return for the combined period is the single year return, R, that is the solution of the following equation: , giving an average percentage return R of 0.0600 or 6.00%.
Types
The table of mathematical symbolsTable of mathematical symbols
This is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...
explains the symbols used below.
| Name | Equation or description |
|---|---|
| Arithmetic mean Arithmetic mean In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space... |
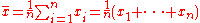 |
| Median Median In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to... |
The middle value that separates the higher half from the lower half of the data set |
| Geometric median Geometric median The geometric median of a discrete set of sample points in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency in higher... |
A rotation Rotation (mathematics) In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming... invariant Invariant (mathematics) In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used... extension of the median Median In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to... for points in Rn |
| Mode Mode (statistics) In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score.... |
The most frequent value in the data set |
| Geometric mean Geometric mean The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the... |
 |
| Harmonic mean Harmonic mean In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired.... |
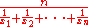 |
| Quadratic mean (or RMS) |
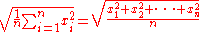 |
| Generalized mean Generalized mean In mathematics, a generalized mean, also known as power mean or Hölder mean , is an abstraction of the Pythagorean means including arithmetic, geometric, and harmonic means.-Definition:... |
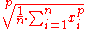 |
| Weighted mean Weighted mean The weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others... |
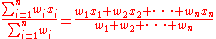 |
| Truncated mean Truncated mean A truncated mean or trimmed mean is a statistical measure of central tendency, much like the mean and median. It involves the calculation of the mean after discarding given parts of a probability distribution or sample at the high and low end, and typically discarding an equal amount of both.For... |
The arithmetic mean of data values after a certain number or proportion of the highest and lowest data values have been discarded |
| Interquartile mean Interquartile mean The interquartile mean is a statistical measure of central tendency, much like the mean , the median, and the mode.... |
A special case of the truncated mean, using the interquartile range Interquartile range In descriptive statistics, the interquartile range , also called the midspread or middle fifty, is a measure of statistical dispersion, being equal to the difference between the upper and lower quartiles... |
| Midrange | 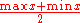 |
| Winsorized mean Winsorized mean A Winsorized mean is a Winsorized statistical measure of central tendency, much like the mean and median, and even more similar to the truncated mean... |
Similar to the truncated mean, but, rather than deleting the extreme values, they are set equal to the largest and smallest values that remain |
| Annualization Compound annual growth rate Compound annual growth rate is a business and investing specific term for the smoothed annualized gain of an investment over a given time period... |
 |
Solutions to variational problems
Several measures of central tendency can be characterized as solving a variational problem, in the sense of the calculus of variationsCalculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, namely minimizing variation from the center. That is, given a measure of statistical dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
, one asks for a measure of central tendency that minimizes variation: such that variation from the center is minimal among all choices of center. In a quip, "dispersion precedes location". In the sense of Lp spaces
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, the correspondence is:
| Lp | dispersion | central tendency |
|---|---|---|
| L1 | average absolute deviation | median Median In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to... |
| L2 | standard deviation Standard deviation Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average... |
mean Mean In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean.... |
| L∞ | maximum deviation | midrange |
Thus standard deviation about the mean is lower than standard deviation about any other point, and the maximum deviation about the midrange is lower than the maximum deviation about any other point. The uniqueness of this characterization of mean follows from convex optimization. Indeed, for a given (fixed) data set x, the function

represents the dispersion about a constant value c relative to the L2 norm. Because the function ƒ2 is a strictly convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
coercive function
Coercive function
In mathematics, a coercive function is a function that "grows rapidly" at the extremes of the space on which it is defined. More precisely, a function f : Rn → Rn is called coercive if...
, the minimizer exists and is unique.
Note that the median in this sense is not in general unique, and in fact any point between the two central points of a discrete distribution minimizes average absolute deviation. The dispersion in the L1 norm, given by

is not strictly convex, whereas strict convexity is needed to ensure uniqueness of the minimizer. In spite of this, the minimizer is unique for the L∞ norm.
Miscellaneous types
Other more sophisticated averages are: trimeanTrimean
In statistics the trimean , or Tukey's trimean, is a measure of a probability distribution's location defined as a weighted average of the distribution's median and its two quartiles:This is equivalent to the average of the median and the midhinge:...
, trimedian, and normalized mean, with their generalizations.
One can create one's own average metric using generalized f-mean:
where f is any invertible function. The harmonic mean is an example of this using f(x) = 1/x, and the geometric mean is another, using f(x) = log x. Another example, expmean (exponential mean) is a mean using the function f(x) = ex, and it is inherently biased towards the higher values. However, this method for generating means is not general enough to capture all averages. A more general method for defining an average, y, takes any function of a list g(x1, x2, ..., xn), which is symmetric under permutation of the members of the list, and equates it to the same function with the value of the average replacing each member of the list: g(x1, x2, ..., xn) = g(y, y, ..., y). This most general definition still captures the important property of all averages that the average of a list of identical elements is that element itself.
The function g(x1, x2, ..., xn) =x1+x2+ ...+ xn provides the arithmetic mean.
The function g(x1, x2, ..., xn) =x1·x2· ...· xn provides the geometric mean.
The function g(x1, x2, ..., xn) =x1−1+x2−1+ ...+ xn−1 provides the harmonic mean. (See John Bibby (1974) “Axiomatisations of the average and a further generalisation of monotonic sequences,” Glasgow Mathematical Journal, vol. 15, pp. 63–65.)
In data streams
The concept of an average can be applied to a stream of data as well as a bounded set, the goal being to find a value about which recent data is in some way clustered. The stream may be distributed in time, as in samples taken by some data acquisition system from which we want to remove noise, or in space, as in pixels in an image from which we want to extract some property. An easy-to-understand and widely used application of average to a stream is the simple moving average in which we compute the arithmetic mean of the most recent N data items in the stream. To advance one position in the stream, we add 1/N times the new data item and subtract 1/N times the data item N places back in the stream.- Update rule for a window of size
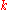 upon seeing new element
upon seeing new element 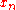 :
:

Averages of functions
The concept of average can be extended to functions. In calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the average value of an integrable
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
function ƒ on an interval [a,b] is defined by
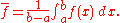
Etymology
An early meaning (c. 1500) of the word average is "damage sustained at sea". The root is found in Arabic as awar, in Italian as avaria, in French as avarie and in Dutch as averij. Hence an average adjuster is a person who assesses an insurable loss.Marine damage is either particular average, which is borne only by the owner of the damaged property, or general average
General average
The law of general average is a legal principle of maritime law according to which all parties in a sea venture proportionally share any losses resulting from a voluntary sacrifice of part of the ship or cargo to save the whole in an emergency...
, where the owner can claim a proportional contribution from all the parties to the marine venture. The type of calculations used in adjusting general average gave rise to the use of "average" to mean "arithmetic mean".
However, according to the Oxford English Dictionary, the earliest usage in English (1489 or earlier) appears to be an old legal term for a tenant's day labour obligation to a sheriff, probably anglicised from "avera" found in the English Domesday Book
Domesday Book
Domesday Book , now held at The National Archives, Kew, Richmond upon Thames in South West London, is the record of the great survey of much of England and parts of Wales completed in 1086...
(1085). This pre-existing term thus lay to hand when an equivalent for avarie was wanted.
See also
- Algorithms for calculating mean and varianceAlgorithms for calculating varianceAlgorithms for calculating variance play a major role in statistical computing. A key problem in the design of good algorithms for this problem is that formulas for the variance may involve sums of squares, which can lead to numerical instability as well as to arithmetic overflow when dealing with...
- Law of averagesLaw of averagesThe law of averages is a lay term used to express a belief that outcomes of a random event will "even out" within a small sample.As invoked in everyday life, the "law" usually reflects bad statistics or wishful thinking rather than any mathematical principle...
- MeanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
- MedianMedianIn probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
- Mode (statistics)Mode (statistics)In statistics, the mode is the value that occurs most frequently in a data set or a probability distribution. In some fields, notably education, sample data are often called scores, and the sample mode is known as the modal score....
- Spherical meanSpherical meanIn mathematics, the spherical mean of a function around a point is the average of all values of that function on a sphere of given radius centered at that point.-Definition:...
- Weighted meanWeighted meanThe weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others...






