Group ring
Encyclopedia
In algebra
, a group ring is a free module
and at the same time a ring
, constructed in a natural way from any given ring and any given group
. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free module and its multiplication extends "by linearity" the given group law on the basis. Less formally, a group ring is a generalization of a given group, by attaching to each element of the group a "weighting factor" from a given ring.
If the given ring is commutative, a group ring is also referred to as a group algebra
, for it is indeed an algebra
over the given ring.
The apparatus of group rings is especially useful in the theory of group representation
s.
, where the product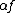
of a scalar 
in R and a vector (or mapping) f is defined as the vector 
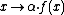, and the sum of two vectors f and g is defined as the vector 
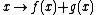. To turn the commutative group R[G] into a ring, we define the product of f and g to be the vector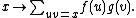
The summation is legitimate because f and g are of finite support, and the ring axioms are readily verified.
Some variations in the notation and terminology are in use. In particular, the mappings such as f : G → R are sometimes written as what are called "formal linear combinations of elements of G, with coefficients in R":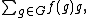
or simply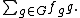
where this doesn't cause confusion.
of three elements with generator a. An element r of C[G] may be written as
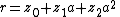
where z0, z1 and z2 are in C, the complex numbers. Writing a different element s as
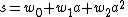
their sum is
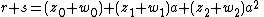
and their product is
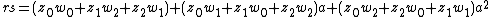
When G is a non-commutative group, one must be careful to preserve the order of the group elements (and not accidentally commute them) when multiplying the terms.
A different example is that of the Laurent polynomials over a ring R: these are nothing more or less than the group ring of the infinite cyclic group Z over R.
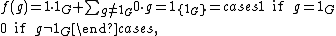
the set of all scalar multiples of f is a subring of R[G] isomorphic to R. And if we map each element s of G to the indicator function of {s}, which is the vector f defined by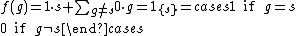
the resulting mapping is an injective group homomorphism (with respect to multiplication, not addition, in R[G]).
If R and G are both commutative (i.e., R is commutative and G is an abelian group
), R[G] is commutative.
If H is a subgroup
of G, then R[H] is a subring
of R[G]. Similarly, if S is a subring of R, S[G] is a subring of R[G].
s of finite group
s. The group algebra K[G] over a field K is essentially the group ring, with the field K taking the place of the ring. As a set and vector space, it is the free vector space over the field, with the elements being formal sums: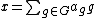
The algebra
structure on the vector space defined by the multiplication in the group: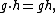
where on the left, g and h indicate elements of the group algebra, while the multiplication on the right is the group operation (written as multiplication).
Because the above multiplication can be confusing, one can also write the basis vectors of K[G] as eg (instead of g), in which case the multiplication is written as: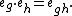
of functions.
While the group algebra of a finite group can be identified with the space of functions on the group, for an infinite group these are different. The group algebra, consisting of finite sums, corresponds to functions on the group that vanish for cofinitely many points; topologically (using the discrete topology), these correspond to functions with compact support.
However, the group algebra K[G] and the space of function KG := Hom(G,K) are dual: given an element of the group algebra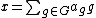
and a function on the group 
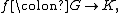these pair to give an element of K via 
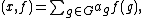which is a well-defined sum because it is finite.
of the group.
Written as a representation, it is the representation g ρg with the action given by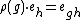
, or
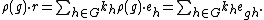
The group algebra C[G] of a finite group over the complex numbers is a semisimple ring. This result, Maschke's theorem
, allows us to understand C[G] as a finite product
of matrix ring
s with entries in C.
Group rings satisfy a universal property
.
Every group ring of a finite group over a field is a Frobenius algebra
, with Frobenius form σ(a,b) the coefficient of the identity element of a·b.
of the algebra over a vector space V. Such a representation
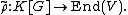
is an algebra homomorphism from the group algebra to the set of endomorphism
s on V. Taking V to be an abelian group
, with group addition given by vector addition, such a representation in fact a left K[G]-module
over the abelian group V. That this is so is exhibited below, where each axiom of a module is demonstrated.
Pick r ∈ K[G] so that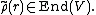
Then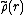
is a homomorphism of abelian groups, in that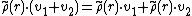
for any v1, v2 ∈ V. Next, one notes that the set of endomorphisms of an abelian group is an endomorphism ring
. The representation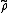
is a ring homomorphism, in that one has
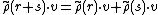
for any two r, s ∈ K[G] and v ∈ V. Similarly, under multiplication,
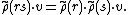
Finally, one has that the unit is mapped to the identity:
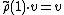
where 1 is the multiplicative unit of K[G]; that is,
is the vector corresponding to the identity element e in G.
The last three equations show that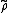
is a ring homomorphism from K[G] taken as a group ring, to the endomorphism ring. The first identity showed that individual elements are group homomorphisms. Thus, a representation 
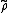is a left K[G]-module over the abelian group V.
Note that given a general K[G]-module, a vector-space structure is induced on V, in that one has an additional axiom
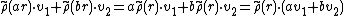
for scalar a, b ∈ K.
Any group representation
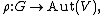
with V a vector space over the field K, can be extended linearly to an algebra representation
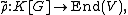
simply by mapping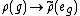
. Thus, representations of the group correspond exactly to representations of the algebra, and so, in a certain sense, talking about the one is the same as talking about the other.
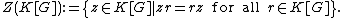
The center is equal to the set of class function
s, that is the set of elements that are constant on each conjugacy class: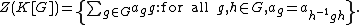
If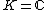
, the set of irreducible characters
of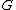
forms an orthonormal basis of 
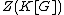with respect to the inner product 
proved that if a and b are elements of C[G] with ab = 1, then ba = 1. Whether this is true if R is a field of positive characteristic remains unknown.
A long-standing conjecture of Kaplansky (~1940) says that if G is a torsion-free group, and K is a field, then the group ring K[G] has no non-trivial zero divisor
s. This conjecture is equivalent to K[G] having no non-trivial nilpotent
s under the same hypotheses for K and G.
In fact, the condition that K is a field can be relaxed to any ring that can be embedded into an integral domain.
The conjecture remains open in full generality, however some special cases of torsion-free groups have been shown to satisfy the zero divisor conjecture. These include:
The case of G being a topological group
is discussed in greater detail in the article on group algebra
s.
of G over the field R. There is no particular reason to limit R to be a field here. However, the classical results were obtained first when R is the complex number
field and G is a finite group, so this case deserves close attention. It was shown that R[G] is a semisimple ring, under those conditions, with profound implications for the representations of finite groups. More generally, whenever the characteristic
of the field R does not divide the order of the finite group G, then R[G] is semisimple (Maschke's theorem
).
When G is a finite abelian group
, the group ring is commutative, and its structure is easy to express in terms of roots of unity
. When R is a field of characteristic p, and the prime number p divides the order of the finite group G, then the group ring is not semisimple: it has a non-zero Jacobson radical
, and this gives the corresponding subject of modular representation theory
its own, deeper character.
, the group ring construction is left adjoint to "group of units"; the following functors are an adjoint pair
:
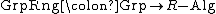
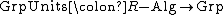
where "GrpRng" takes a group to its group ring over R, and "GrpUnits" takes an R-algebra to its group of units.
When R = Z, this gives an adjunction between the category of groups
and the category of rings
, and the unit of the adjunction takes a group G to a group that contains trivial units: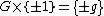
. In general, group rings contain nontrivial units. If G contains elements a and b such that 
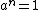and b does not normalize 
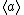then the square of 
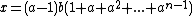is zero, hence 
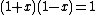. The element 
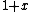is a unit of infinite order.
, of which another example is the incidence algebra
.
– for example, if there is a choice of generators and one takes the word metric, as in Coxeter group
s – then the group ring becomes a filtered algebra
.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, a group ring is a free module
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
and at the same time a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, constructed in a natural way from any given ring and any given group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free module and its multiplication extends "by linearity" the given group law on the basis. Less formally, a group ring is a generalization of a given group, by attaching to each element of the group a "weighting factor" from a given ring.
If the given ring is commutative, a group ring is also referred to as a group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
, for it is indeed an algebra
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
over the given ring.
The apparatus of group rings is especially useful in the theory of group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s.
Definition
Let G be a group, written multiplicatively, and let R a ring. The group ring of G over R, which we will denote by R[G], is the set of mappings f : G → R of finite supportSupport (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
, where the product
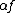of a scalar in R and a vector (or mapping) f is defined as the vector 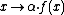, and the sum of two vectors f and g is defined as the vector 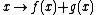. To turn the commutative group R[G] into a ring, we define the product of f and g to be the vector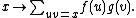The summation is legitimate because f and g are of finite support, and the ring axioms are readily verified.
Some variations in the notation and terminology are in use. In particular, the mappings such as f : G → R are sometimes written as what are called "formal linear combinations of elements of G, with coefficients in R":
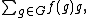
or simply
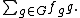
where this doesn't cause confusion.
Two simple examples
Let G = Z3, the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of three elements with generator a. An element r of C[G] may be written as
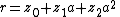
where z0, z1 and z2 are in C, the complex numbers. Writing a different element s as
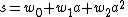
their sum is
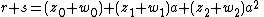
and their product is
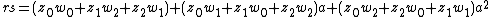
When G is a non-commutative group, one must be careful to preserve the order of the group elements (and not accidentally commute them) when multiplying the terms.
A different example is that of the Laurent polynomials over a ring R: these are nothing more or less than the group ring of the infinite cyclic group Z over R.
Some basic properties
Assuming that the ring R has a unit element 1, and denoting the group unit by 1G, the ring R[G] contains a subring isomorphic to R, and its group of invertible elements contains a subgroup isomorphic to G. For considering the indicator function of {1G}, which is the vector f defined by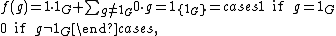the set of all scalar multiples of f is a subring of R[G] isomorphic to R. And if we map each element s of G to the indicator function of {s}, which is the vector f defined by
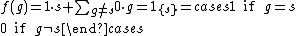
the resulting mapping is an injective group homomorphism (with respect to multiplication, not addition, in R[G]).
If R and G are both commutative (i.e., R is commutative and G is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
), R[G] is commutative.
If H is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G, then R[H] is a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of R[G]. Similarly, if S is a subring of R, S[G] is a subring of R[G].
Group algebra over a finite group
Group algebras occur naturally in the theory of group representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s. The group algebra K[G] over a field K is essentially the group ring, with the field K taking the place of the ring. As a set and vector space, it is the free vector space over the field, with the elements being formal sums:
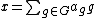
The algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
structure on the vector space defined by the multiplication in the group:
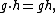
where on the left, g and h indicate elements of the group algebra, while the multiplication on the right is the group operation (written as multiplication).
Because the above multiplication can be confusing, one can also write the basis vectors of K[G] as eg (instead of g), in which case the multiplication is written as:
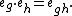
Interpretation as functions
Thinking of the free vector space as K-valued functions on G, the algebra multiplication is convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of functions.
While the group algebra of a finite group can be identified with the space of functions on the group, for an infinite group these are different. The group algebra, consisting of finite sums, corresponds to functions on the group that vanish for cofinitely many points; topologically (using the discrete topology), these correspond to functions with compact support.
However, the group algebra K[G] and the space of function KG := Hom(G,K) are dual: given an element of the group algebra
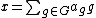and a function on the group 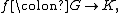these pair to give an element of K via 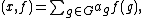which is a well-defined sum because it is finite.Regular representation
The group algebra is an algebra over itself; under the correspondence of representations over R and R[G] modules, it is the regular representationRegular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
of the group.
Written as a representation, it is the representation g ρg with the action given by
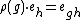, or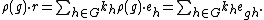Properties
The dimension of the vector space K[G] is just equal to the number of elements in the group. The field K is commonly taken to be the complex numbers C or the reals R, so that one discusses the group algebras C[G] or R[G].The group algebra C[G] of a finite group over the complex numbers is a semisimple ring. This result, Maschke's theorem
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
, allows us to understand C[G] as a finite product
Product of rings
In mathematics, it is possible to combine several rings into one large product ring. This is done as follows: if I is some index set and Ri is a ring for every i in I, then the cartesian product Πi in I Ri can be turned into a ring by defining the operations coordinatewise, i.e...
of matrix ring
Matrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
s with entries in C.
Group rings satisfy a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
.
Every group ring of a finite group over a field is a Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
, with Frobenius form σ(a,b) the coefficient of the identity element of a·b.
Representations of a group algebra
Taking K[G] to be an abstract algebra, one may ask for concrete representationsGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the algebra over a vector space V. Such a representation
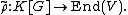
is an algebra homomorphism from the group algebra to the set of endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s on V. Taking V to be an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, with group addition given by vector addition, such a representation in fact a left K[G]-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the abelian group V. That this is so is exhibited below, where each axiom of a module is demonstrated.
Pick r ∈ K[G] so that
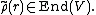
Then
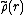is a homomorphism of abelian groups, in that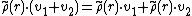for any v1, v2 ∈ V. Next, one notes that the set of endomorphisms of an abelian group is an endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
. The representation
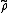is a ring homomorphism, in that one has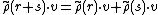for any two r, s ∈ K[G] and v ∈ V. Similarly, under multiplication,
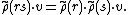
Finally, one has that the unit is mapped to the identity:
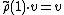
where 1 is the multiplicative unit of K[G]; that is,
is the vector corresponding to the identity element e in G.
The last three equations show that
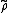is a ring homomorphism from K[G] taken as a group ring, to the endomorphism ring. The first identity showed that individual elements are group homomorphisms. Thus, a representation 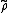is a left K[G]-module over the abelian group V.Note that given a general K[G]-module, a vector-space structure is induced on V, in that one has an additional axiom
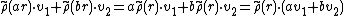
for scalar a, b ∈ K.
Any group representation
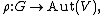
with V a vector space over the field K, can be extended linearly to an algebra representation
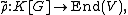
simply by mapping
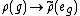. Thus, representations of the group correspond exactly to representations of the algebra, and so, in a certain sense, talking about the one is the same as talking about the other.Center of a group algebra
The center of the group algebra is the set of elements that commute with all elements of the group algebra: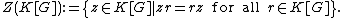The center is equal to the set of class function
Class function
In mathematics, especially in the fields of group theory and representation theory of groups, a class function is a function f on a group G, such that f is constant on the conjugacy classes of G. In other words, f is invariant under the conjugation map on G...
s, that is the set of elements that are constant on each conjugacy class:
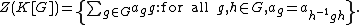
If
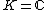, the set of irreducible charactersCharacter theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
of
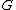forms an orthonormal basis of 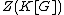with respect to the inner product Group rings over an infinite group
Much less is known in the case where G is countably infinite, or uncountable, and this is an area of active research. The case where R is the field of complex numbers is probably the one best studied. In this case, Irving KaplanskyIrving Kaplansky
Irving Kaplansky was a Canadian mathematician.-Biography:He was born in Toronto, Ontario, Canada, after his parents emigrated from Poland and attended the University of Toronto as an undergraduate. After receiving his Ph.D...
proved that if a and b are elements of C[G] with ab = 1, then ba = 1. Whether this is true if R is a field of positive characteristic remains unknown.
A long-standing conjecture of Kaplansky (~1940) says that if G is a torsion-free group, and K is a field, then the group ring K[G] has no non-trivial zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s. This conjecture is equivalent to K[G] having no non-trivial nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
s under the same hypotheses for K and G.
In fact, the condition that K is a field can be relaxed to any ring that can be embedded into an integral domain.
The conjecture remains open in full generality, however some special cases of torsion-free groups have been shown to satisfy the zero divisor conjecture. These include:
- Unique product groups (which include virtually abelian groups, orderable groups, and free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s, since they are orderable)
- Elementary amenable groupElementary amenable groupIn mathematics, a group is called elementary amenable if it can be built up from finite groups and abelian groups by a sequence of simple operations that result in amenable groups when applied to amenable groups...
s
- Diffuse groups - in particular, groups that act freely isometrically on R-trees, and the fundamental groups of surface groups except for the fundamental groups of direct sums of one, two or three copies of the projective plane.
The case of G being a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
is discussed in greater detail in the article on group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
s.
Representations of a group ring
A module M over R[G] is then the same as a linear representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G over the field R. There is no particular reason to limit R to be a field here. However, the classical results were obtained first when R is the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
field and G is a finite group, so this case deserves close attention. It was shown that R[G] is a semisimple ring, under those conditions, with profound implications for the representations of finite groups. More generally, whenever the characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of the field R does not divide the order of the finite group G, then R[G] is semisimple (Maschke's theorem
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
).
When G is a finite abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, the group ring is commutative, and its structure is easy to express in terms of roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
. When R is a field of characteristic p, and the prime number p divides the order of the finite group G, then the group ring is not semisimple: it has a non-zero Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
, and this gives the corresponding subject of modular representation theory
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
its own, deeper character.
Adjoint
CategoricallyCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the group ring construction is left adjoint to "group of units"; the following functors are an adjoint pair
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
:
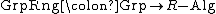
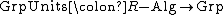
where "GrpRng" takes a group to its group ring over R, and "GrpUnits" takes an R-algebra to its group of units.
When R = Z, this gives an adjunction between the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
and the category of rings
Category of rings
In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms...
, and the unit of the adjunction takes a group G to a group that contains trivial units:
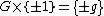. In general, group rings contain nontrivial units. If G contains elements a and b such that 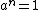and b does not normalize 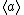then the square of 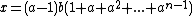is zero, hence 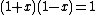. The element 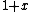is a unit of infinite order.Generalizations
The group algebra generalizes to the monoid ring and thence to the categorical algebraCategorical algebra
In category theory, a field of mathematics, a categorical algebra is an associative algebra, defined for any locally finite category and commutative ring with unity.It generalizes the notions of group algebra and incidence algebra,...
, of which another example is the incidence algebra
Incidence algebra
In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
.
Filtration
If a group has a length functionLength function
In mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
– for example, if there is a choice of generators and one takes the word metric, as in Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s – then the group ring becomes a filtered algebra
Filtered algebra
In mathematics, a filtered algebra is a generalization of the notion of a graded algebra. Examples appear in many branches of mathematics, especially in homological algebra and representation theory....
.