Associative algebra
Encyclopedia
In mathematics
, an associative algebra A is an associative ring
that has a compatible structure of a vector space over a certain field
K or, more generally, of a module
over a commutative ring
R. Thus A is endowed with binary operations of addition and multiplication satisfying a number of axioms, including associativity
of multiplication and distributivity
, as well as compatible multiplication by the elements of the field K or the ring R.
In some areas of mathematics, associative algebras are typically assumed to have a multiplicative unit, denoted 1. To make this extra assumption clear, these associative algebras are called unital algebras.
. An associative R-algebra is an additive abelian group
A which has the structure of both a ring
and an R-module
in such a way that ring multiplication is R-bilinear: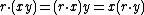
for all r ∈ R and x, y ∈ A.
We say A is unital if it contains an element 1 such that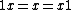
for all x ∈ A.
If A itself is commutative (as a ring) then it is called a commutative R-algebra.
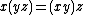
for all x, y, and z in A. This R-bilinear mapping then gives A the structure of a ring and an associative R-algebra. Every associative R-algebra arises this way.
Moreover, the algebra A built this way will be unital if and only if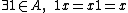
This definition is equivalent to the statement that a unital associative R-algebra is a monoid
in R-Mod (the monoidal category
of R-modules).
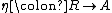whose image lies in the center
of A. The algebra A can then be thought of as an R-module by defining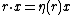
for all r ∈ R and x ∈ A.
If A is commutative then the center of A is equal to A, so that a commutative R-algebra can be defined simply as a homomorphism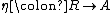
of commutative rings.
between two associative R-algebras is an R-linear ring homomorphism
. Explicitly,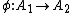
is an associative algebra homomorphism if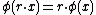
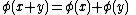
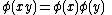
For a homomorphism of unital associative R-algebras, we also demand that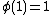
The class of all unital associative R-algebras together with algebra homomorphisms between them form a category
, sometimes denoted R-Alg.
The subcategory
of commutative R-algebras can be characterized as the coslice category R/CRing where CRing is the category of commutative rings.
and a submodule of A. That is, it must be closed under addition, ring multiplication, scalar multiplication, and it must contain the identity element of A.
Quotient algebras: Let A be an R-algebra. Any ring-theoretic ideal
I in A is automatically an R-module since r·x = (r1A)x. This gives the quotient ring
A/I the structure of an R-module and, in fact, an R-algebra. It follows that any ring homomorphic image of A is also an R-algebra.
Direct products: The direct product of a family of R-algebras is the ring-theoretic direct product. This becomes an R-algebra with the obvious scalar multiplication.
Free products: One can form a free product
of R-algebras in a manner similar to the free product of groups. The free product is the coproduct
in the category of R-algebras.
Tensor products: The tensor product of two R-algebras is also an R-algebra in a natural way. See tensor product of algebras
for more details.
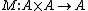
An associative algebra is an algebra where the map M has the property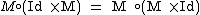
Here, the symbol
refers to function composition
, and Id : A → A is the identity map
on A.
To see the equivalence of the definitions, we need only understand that each side of the above equation is a function that takes three arguments. For example, the left-hand side acts as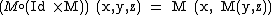
Similarly, a unital associative algebra can be defined in terms of a unit map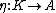
which has the property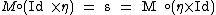
Here, the unit map η takes an element k in K to the element k1 in A, where 1 is the unit element of A. The map s is just plain-old scalar multiplication: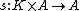
; thus, the above identity is sometimes written with Id standing in the place of s, with scalar multiplication being implicitly understood.
A×A→A having 2 inputs (multiplicator and multiplicand) and one output (product), as well as a morphism K→A identifying the scalar multiples of the multiplicative identity. These two morphisms can be dualized using categorial duality by reversing all arrows in the commutative diagram
s which describe the algebra axiom
s; this defines the structure of a coalgebra
.
There is also an abstract notion of F-coalgebra
.
of an algebra is a linear map ρ: A → gl(V) from A to the general linear algebra of some vector space (or module) V that preserves the multiplicative operation: that is, ρ(xy)=ρ(x)ρ(y).
Note, however, that there is no natural way of defining a tensor product
of representations of associative algebras, without somehow imposing additional conditions. Here, by tensor product of representations, the usual meaning is intended: the result should be a linear representation on the product vector space. Imposing such additional structure typically leads to the idea of a Hopf algebra
or a Lie algebra
, as demonstrated below.
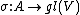and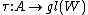 
. One might try to form a tensor product representation 
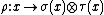according to how it acts on the product vector space, so that
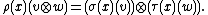
However, such a map would not be linear, since one would have
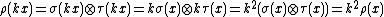
for k ∈ K. One can rescue this attempt and restore linearity by imposing additional structure, by defining a map Δ: A → A × A, and defining the tensor product representation as
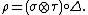
Here, Δ is a comultiplication. The resulting structure is called a bialgebra
. To be consistent with the definitions of the associative algebra, the coalgebra must be co-associative, and, if the algebra is unital, then the co-algebra must be unital as well. Note that bialgebras leave multiplication and co-multiplication unrelated; thus it is common to relate the two (by defining an antipode), thus creating a Hopf algebra
.
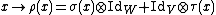
so that the action on the tensor product space is given by
.
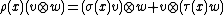This map is clearly linear in x, and so it does not have the problem of the earlier definition. However, it fails to preserve multiplication:
.
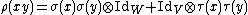But, in general, this does not equal
.
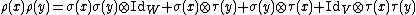Equality would hold if the product xy were antisymmetric (if the product were the Lie bracket
, that is,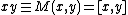
), thus turning the associative algebra into a Lie algebra
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an associative algebra A is an associative ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
that has a compatible structure of a vector space over a certain field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K or, more generally, of a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R. Thus A is endowed with binary operations of addition and multiplication satisfying a number of axioms, including associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
of multiplication and distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
, as well as compatible multiplication by the elements of the field K or the ring R.
In some areas of mathematics, associative algebras are typically assumed to have a multiplicative unit, denoted 1. To make this extra assumption clear, these associative algebras are called unital algebras.
Formal definition
Let R be a fixed commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. An associative R-algebra is an additive abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
A which has the structure of both a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and an R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
in such a way that ring multiplication is R-bilinear:
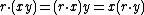
for all r ∈ R and x, y ∈ A.
We say A is unital if it contains an element 1 such that
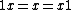
for all x ∈ A.
If A itself is commutative (as a ring) then it is called a commutative R-algebra.
From R-modules
Starting with an R-module A, we get an associative R-algebra by equipping A with an R-bilinear mapping A × A → A such that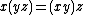for all x, y, and z in A. This R-bilinear mapping then gives A the structure of a ring and an associative R-algebra. Every associative R-algebra arises this way.
Moreover, the algebra A built this way will be unital if and only if
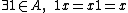
This definition is equivalent to the statement that a unital associative R-algebra is a monoid
Monoid (category theory)
In category theory, a monoid in a monoidal category is an object M together with two morphisms* \mu : M\otimes M\to M called multiplication,* and \eta : I\to M called unit,...
in R-Mod (the monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
of R-modules).
From rings
Starting with a ring A, we get a unital associative R-algebra by providing a ring homomorphismRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
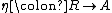whose image lies in the centerCenter (algebra)
The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
of A. The algebra A can then be thought of as an R-module by defining
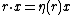
for all r ∈ R and x ∈ A.
If A is commutative then the center of A is equal to A, so that a commutative R-algebra can be defined simply as a homomorphism
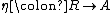of commutative rings.Algebra homomorphisms
A homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
between two associative R-algebras is an R-linear ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
. Explicitly,
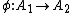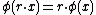
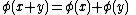
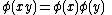
is an associative algebra homomorphism ifFor a homomorphism of unital associative R-algebras, we also demand that
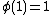
The class of all unital associative R-algebras together with algebra homomorphisms between them form a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, sometimes denoted R-Alg.
The subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of commutative R-algebras can be characterized as the coslice category R/CRing where CRing is the category of commutative rings.
Examples
- The square n-by-n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with entries from the field K form a unitary associative algebra over K. - The complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s form a 2-dimensional unitary associative algebra over the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. - The quaternions form a 4-dimensional unitary associative algebra over the reals (but not an algebra over the complex numbers, since if complex numbers are treated as a subset of the quaternions, complex numbers and quaternions do not commute).
- The 2 × 2 real matrices form an associative algebra useful in plane mapping.
- The polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with real coefficients form a unitary associative algebra over the reals. - Given any Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
X, the continuous linear operators A : X → X form a unitary associative algebra (using composition of operators as multiplication); this is a Banach algebraBanach algebraIn mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
. - Given any topological spaceTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
X, the continuous real- or complex-valued functions on X form a real or complex unitary associative algebra; here the functions are added and multiplied pointwise. - An example of a non-unitary associative algebra is given by the set of all functions f: R → R whose limitLimit of a functionIn mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
as x nears infinity is zero. - The Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s, which are useful in geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. - Incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
s of locally finite partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s are unitary associative algebras considered in combinatoricsCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
. - Any ring A can be considered as a Z-algebra in a unique way. The unique ring homomorphism from Z to A is determined by the fact that it must send 1 to the identity in A. Therefore rings and Z-algebras are equivalent concepts, in the same way that abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s and Z-modules are equivalent. - Any ring of characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
n is a (Z/nZ)-algebra in the same way. - Any ring A is an algebra over its centerCenter (algebra)The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
Z(A), or over any subring of its center. - Any commutative ring R is an algebra over itself, or any subring of R.
- Given an R-module M, the endomorphism ringEndomorphism ringIn abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of M, denoted EndR(M) is an R-algebra by defining (r·φ)(x) = r·φ(x). - Any ring of matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with coefficients in a commutative ring R forms an R-algebra under matrix addition and multiplication. This coincides with the previous example when M is a finitely-generated, freeFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
R-module. - Every polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[x1, ..., xn] is a commutative R-algebra. In fact, this is the free commutative R-algebra on the set {x1, ..., xn}. - The free R-algebraFree algebraIn mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring .-Definition:...
on a set E is an algebra of polynomials with coefficients in R and noncommuting indeterminates taken from the set E. - The tensor algebraTensor algebraIn mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
of an R-module is naturally an R-algebra. The same is true for quotients such as the exteriorExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
and symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
s. Categorically speaking, the functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
which maps an R-module to its tensor algebra is left adjoint to the functor which sends an R-algebra to its underlying R-module (forgetting the ring structure). - Given a commutative ring R and any ring A the tensor product R⊗ZA can be given the structure of an R-algebra by defining r·(s⊗a) = (rs⊗a). The functor which sends A to R⊗ZA is left adjoint to the functor which sends an R-algebra to its underlying ring (forgetting the module structure).
Constructions
Subalgebras: A subalgebra of an R-algebra A is a subset of A which is both a subringSubring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
and a submodule of A. That is, it must be closed under addition, ring multiplication, scalar multiplication, and it must contain the identity element of A.
Quotient algebras: Let A be an R-algebra. Any ring-theoretic ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
I in A is automatically an R-module since r·x = (r1A)x. This gives the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
A/I the structure of an R-module and, in fact, an R-algebra. It follows that any ring homomorphic image of A is also an R-algebra.
Direct products: The direct product of a family of R-algebras is the ring-theoretic direct product. This becomes an R-algebra with the obvious scalar multiplication.
Free products: One can form a free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
of R-algebras in a manner similar to the free product of groups. The free product is the coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in the category of R-algebras.
Tensor products: The tensor product of two R-algebras is also an R-algebra in a natural way. See tensor product of algebras
Tensor product of algebras
In mathematics, the tensor product of two R-algebras is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras....
for more details.
Associativity and the multiplication mapping
Associativity was defined above quantifying over all elements of A. It is possible to define associativity in a way that does not explicitly refer to elements. An algebra is defined as a map M (multiplication) on a vector space A: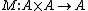An associative algebra is an algebra where the map M has the property
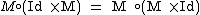
Here, the symbol
refers to function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, and Id : A → A is the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on A.
To see the equivalence of the definitions, we need only understand that each side of the above equation is a function that takes three arguments. For example, the left-hand side acts as
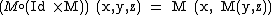
Similarly, a unital associative algebra can be defined in terms of a unit map
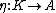
which has the property
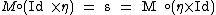
Here, the unit map η takes an element k in K to the element k1 in A, where 1 is the unit element of A. The map s is just plain-old scalar multiplication:
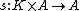; thus, the above identity is sometimes written with Id standing in the place of s, with scalar multiplication being implicitly understood.Coalgebras
An associative unitary algebra over K is based on a morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
A×A→A having 2 inputs (multiplicator and multiplicand) and one output (product), as well as a morphism K→A identifying the scalar multiples of the multiplicative identity. These two morphisms can be dualized using categorial duality by reversing all arrows in the commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
s which describe the algebra axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s; this defines the structure of a coalgebra
Coalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
.
There is also an abstract notion of F-coalgebra
F-coalgebra
In mathematics, specifically in category theory, an F-coalgebra is a structure defined according to a functor F. For both algebra and coalgebra, a functor is a convenient and general way of organizing a signature...
.
Representations
A representationRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of an algebra is a linear map ρ: A → gl(V) from A to the general linear algebra of some vector space (or module) V that preserves the multiplicative operation: that is, ρ(xy)=ρ(x)ρ(y).
Note, however, that there is no natural way of defining a tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of representations of associative algebras, without somehow imposing additional conditions. Here, by tensor product of representations, the usual meaning is intended: the result should be a linear representation on the product vector space. Imposing such additional structure typically leads to the idea of a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
or a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, as demonstrated below.
Motivation for a Hopf algebra
Consider, for example, two representations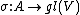 and 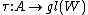. One might try to form a tensor product representation 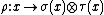according to how it acts on the product vector space, so that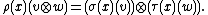However, such a map would not be linear, since one would have
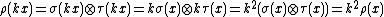
for k ∈ K. One can rescue this attempt and restore linearity by imposing additional structure, by defining a map Δ: A → A × A, and defining the tensor product representation as
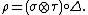
Here, Δ is a comultiplication. The resulting structure is called a bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
. To be consistent with the definitions of the associative algebra, the coalgebra must be co-associative, and, if the algebra is unital, then the co-algebra must be unital as well. Note that bialgebras leave multiplication and co-multiplication unrelated; thus it is common to relate the two (by defining an antipode), thus creating a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
.
Motivation for a Lie algebra
One can try to be more clever in defining a tensor product. Consider, for example,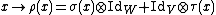so that the action on the tensor product space is given by
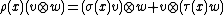.This map is clearly linear in x, and so it does not have the problem of the earlier definition. However, it fails to preserve multiplication:
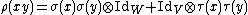.But, in general, this does not equal
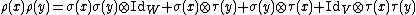.Equality would hold if the product xy were antisymmetric (if the product were the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
, that is,
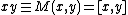), thus turning the associative algebra into a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
.