
Algebraic group
Encyclopedia
In algebraic geometry
, an algebraic group (or group variety) is a group
that is an algebraic variety
, such that the multiplication and inverse are given by regular function
s on the variety. In category theoretic
terms, an algebraic group is a group object
in the category
of algebraic varieties
.
Two important classes of algebraic groups arise, that for the most part are studied separately: abelian varieties
(the 'projective' theory) and linear algebraic group
s (the 'affine' theory). There are certainly examples that are neither one nor the other — these occur for example in the modern theory of integrals of the second and third kinds
such as the Weierstrass zeta function, or the theory of generalized Jacobian
s. But according to a basic theorem any algebraic group is an extension of an abelian variety
by a linear algebraic group. This is a result of Claude Chevalley
: if K is a perfect field
, and G an algebraic group over K, there exists a unique normal closed subgroup H in G, such that H is a linear group and G/H an abelian variety.
According to another basic theorem, any group in the category of affine varieties has a faithful linear representation: we can consider it to be a matrix group over K, defined by polynomials over K and with matrix multiplication as the group operation. For that reason a concept of affine algebraic group is redundant over a field — we may as well use a very concrete definition. Note that this means that algebraic group is narrower than Lie group
, when working over the field of real numbers: there are examples such as the universal cover of the 2×2 special linear group that are Lie groups, but have no faithful linear representation. A more obvious difference between the two concepts arises because the identity component
of an affine algebraic group G is necessarily of finite index
in G.
When one wants to work over a base ring R (commutative), there is the group scheme
concept: that is, a group object
in the category of scheme
s over R. Affine group scheme is the concept dual to a type of Hopf algebra
. There is quite a refined theory of group schemes, that enters for example in the contemporary theory of abelian varieties.
subgroup
.
Generally these are taken to be connected (or irreducible as a variety) as well.
Another way of expressing the condition is as a subgroup
which is also a subvariety
.
This may also be generalized by allowing schemes
in place of varieties. The main effect of this in practice, apart from allowing subgroups in which the connected component
is of finite index > 1, is to admit non-reduced schemes, in characteristic p.
s – for instance, the number of elements of the symmetric group is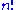 , and the number of elements of the general linear group over a finite field is the q-factorial
, and the number of elements of the general linear group over a finite field is the q-factorial 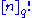 ; thus the symmetric group behaves as though it were a linear group over "the field with one element". This is formalized by the field with one element
; thus the symmetric group behaves as though it were a linear group over "the field with one element". This is formalized by the field with one element
, which considers Coxeter groups to be simple algebraic groups over the field with one element.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, an algebraic group (or group variety) is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
that is an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, such that the multiplication and inverse are given by regular function
Regular function
In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
s on the variety. In category theoretic
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
terms, an algebraic group is a group object
Group object
In category theory, a branch of mathematics, group objects are certain generalizations of groups which are built on more complicated structures than sets...
in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
.
Classes
Several important classes of groups are algebraic groups, including:- Finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s - GLnC, the general linear groupGeneral linear groupIn mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of invertible matrices over C - Elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s
Two important classes of algebraic groups arise, that for the most part are studied separately: abelian varieties
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
(the 'projective' theory) and linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
s (the 'affine' theory). There are certainly examples that are neither one nor the other — these occur for example in the modern theory of integrals of the second and third kinds
Differential of the first kind
In mathematics, differential of the first kind is a traditional term used in the theories of Riemann surfaces and algebraic curves , for everywhere-regular differential 1-forms...
such as the Weierstrass zeta function, or the theory of generalized Jacobian
Generalized Jacobian
- In algebraic geometry :In mathematics, there are several notions of generalized Jacobians, which are algebraic groups or complex manifolds that are in some sense analogous to the Jacobian variety of an algebraic curve, or related to the Albanese variety and Picard variety that generalize it to...
s. But according to a basic theorem any algebraic group is an extension of an abelian variety
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
by a linear algebraic group. This is a result of Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
: if K is a perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
, and G an algebraic group over K, there exists a unique normal closed subgroup H in G, such that H is a linear group and G/H an abelian variety.
According to another basic theorem, any group in the category of affine varieties has a faithful linear representation: we can consider it to be a matrix group over K, defined by polynomials over K and with matrix multiplication as the group operation. For that reason a concept of affine algebraic group is redundant over a field — we may as well use a very concrete definition. Note that this means that algebraic group is narrower than Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, when working over the field of real numbers: there are examples such as the universal cover of the 2×2 special linear group that are Lie groups, but have no faithful linear representation. A more obvious difference between the two concepts arises because the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
of an affine algebraic group G is necessarily of finite index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
in G.
When one wants to work over a base ring R (commutative), there is the group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
concept: that is, a group object
Group object
In category theory, a branch of mathematics, group objects are certain generalizations of groups which are built on more complicated structures than sets...
in the category of scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s over R. Affine group scheme is the concept dual to a type of Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
. There is quite a refined theory of group schemes, that enters for example in the contemporary theory of abelian varieties.
Algebraic subgroup
An algebraic subgroup of an algebraic group is a Zariski closedZariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
.
Generally these are taken to be connected (or irreducible as a variety) as well.
Another way of expressing the condition is as a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
which is also a subvariety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
.
This may also be generalized by allowing schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
in place of varieties. The main effect of this in practice, apart from allowing subgroups in which the connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
is of finite index > 1, is to admit non-reduced schemes, in characteristic p.
Coxeter groups
There are a number of analogous results between algebraic groups and Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s – for instance, the number of elements of the symmetric group is
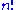 , and the number of elements of the general linear group over a finite field is the q-factorial
, and the number of elements of the general linear group over a finite field is the q-factorial 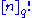 ; thus the symmetric group behaves as though it were a linear group over "the field with one element". This is formalized by the field with one element
; thus the symmetric group behaves as though it were a linear group over "the field with one element". This is formalized by the field with one elementField with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
, which considers Coxeter groups to be simple algebraic groups over the field with one element.
See also
- Algebraic topology (object)Algebraic topology (object)In mathematics, the algebraic topology on the set of group representations from G to a topological group H is the topology of pointwise convergence, i.e...
- Borel subgroupBorel subgroupIn the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
- Tame groupTame groupIn mathematical group theory, a tame group is a certain kind of group defined in model theory.Formally, we define a bad field as a structure of the form , where K is an algebraically closed field and T is an infinite, proper, distinguished subgroup of K, such that is of finite Morley rank in its...
- Morley rankMorley rankIn mathematical logic, Morley rank, introduced by , is a means of measuring the size of a subset of a model of a theory, generalizing the notion of dimension in algebraic geometry.-Definition:Fix a theory T with a model M...
- Cherlin–Zilber conjecture
- Adelic algebraic groupAdelic algebraic groupIn abstract algebra, an adelic algebraic group is a topological group defined by an algebraic group G over a number field K, and the adele ring A = A of K. It consists of the points of G having values in A; the definition of the appropriate topology is straightforward only in case G is a linear...
- Glossary of algebraic groupsGlossary of algebraic groupsThere are a number of mathematical notions to study and classify algebraic groups.In the sequel, G denotes an algebraic group over a field k....

