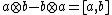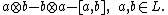Universal enveloping algebra
Encyclopedia
In mathematics
, for any Lie algebra
L one can construct its universal enveloping algebra U(L). This construction passes from the non-associative structure L to a (more familiar, and possibly easier to handle) unital associative algebra
which captures the important properties of L.
Any associative algebra A over the field
K becomes a Lie algebra over K with the Lie bracket:
That is, from an associative product, one can construct a Lie bracket by taking the commutator
with respect to that associative product. Denote this Lie algebra by AL.
Construction of the universal enveloping algebra attempts to reverse this process: to a given Lie algebra L over K, find the "most general" unital associative K-algebra A such that the Lie algebra AL contains L; this algebra A is U(L). The important constraint is to preserve the representation theory: the representations
of L correspond in a one-to-one manner to the module
s over U(L). In a typical context where L is acting by infinitesimal transformation
s, the elements of U(L) act like differential operator
s, of all orders.
appearance in applications is representation of the Lie algebra. A representation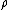 assigns to any element x
assigns to any element x
of a Lie algebra a linear operator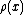 . The space of linear operators
. The space of linear operators
is not only a Lie algebra, but also an associative algebra and so one can consider products . The main point to introduce the universal enveloping algebra is to study such products in various representations of a Lie algebra.
. The main point to introduce the universal enveloping algebra is to study such products in various representations of a Lie algebra.
One obstacle can be immediately seen in a naive attempt to do this:
properties of products drastically depend on the representation, not only on the Lie algebra itself. For example for one representation we might have
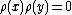 , while in another representation this product may not be zero.
, while in another representation this product may not be zero.
Nevertheless it appears to be true that certain properties are universal for all representations, i.e. they hold true for all representations simultaneously. The universal enveloping algebra is a way to grasp all such properties and only them.
(notation as above) we say that U is the universal enveloping algebra of X if it satisfies the following universal property
: for any unital associative K-algebra A and Lie algebra homomorphism
there exists a unique unital algebra homomorphism
such that
This is the universal property expressing that the functor
sending X to its universal enveloping algebra is left adjoint to the functor sending a unital associative algebra A to its Lie algebra AL.
By the following construction, which suggests itself on general grounds (for instance, as part of a pair of adjoint functors
), we establish that indeed every Lie algebra does have a universal enveloping algebra.
Starting with the tensor algebra
T(L) on the vector space
underlying L, we take U(L) to be the quotient of T(L) made by imposing the relations
for all a and b in (the image in T(L) of) L, where the bracket on the RHS
means the given Lie algebra product, in L.
Formally, we define
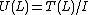
where I is the two-sided ideal
of T(L) generated by elements of the form
The natural map L → T(L) descends to a map h : L → U(L), and this is the Lie algebra homomorphism used in the universal property given above.
The analogous construction for Lie superalgebra
s is straightforward.
of the vector space
L has been chosen, then U(L) can be identified with the polynomial
algebra over K, with one variable per basis element.
If L is the Lie algebra corresponding to the Lie group
G, U(L) can be identified with the algebra of left-invariant differential operator
s (of all orders) on G; with L lying inside it as the left-invariant vector field
s as first-order differential operators.
To relate the above two cases: if L is a vector space V as abelian Lie algebra, the left-invariant differential operators are the constant coefficient operators, which are indeed a polynomial algebra in the partial derivative
s of first order.
The center of U(L) is called Z(L) and consists of the left- and right- invariant differential operators; this in the case of G not commutative will often not be generated by first-order operators (see for example Casimir operator of a semi-simple Lie algebra).
Another characterisation in Lie group theory is of U(L) as the convolution
algebra of distribution
s supported only at the identity element
e of G.
The algebra of differential operators in n variables with polynomial coefficients may be obtained starting with the Lie algebra of the Heisenberg group. See Weyl algebra for this; one must take a quotient, so that the central elements of the Lie algebra act as prescribed scalars.
gives a precise description of U(L); the most important consequence is that L can be viewed as a linear subspace
of U(L). More precisely: the canonical map h : L → U(L) is always injective. Furthermore, U(L) is generated as a unital associative algebra by L.
L acts on itself by the Lie algebra adjoint representation, and this action can be extended to a representation
of L on U(L): L acts as an algebra of derivation
s on T(L), and this action respects the imposed relations, so it actually acts on U(L). (This is the purely infinitesimal way of looking at the invariant differential operators mentioned above.)
Under this representation, the elements of U(L) invariant under the action of L (i.e. such that any element of L acting on them gives zero) are called invariant elements. They are generated by the Casimir invariant
s.
As mentioned above, the construction of universal enveloping algebras is part of a pair of adjoint functors. U is a functor from the category of Lie algebras over K to the category of unital associative K-algebras. This functor is left adjoint to the functor which maps an algebra A to the Lie algebra AL. The universal enveloping algebra construction is not exactly inverse to the formation of AL: if we start with an associative algebra A, then U(AL) is not equal to A; it is much bigger.
The facts about representation theory mentioned earlier can be made precise as follows: the abelian category
of all representations
of L is isomorphic
to the abelian category of all left modules over U(L).
The construction of the group algebra
for a given group
is in many ways analogous to constructing the universal enveloping algebra for a given Lie algebra. Both constructions are universal and translate representation theory into module theory. Furthermore, both group algebras and universal enveloping algebras carry natural comultiplications
which turn them into Hopf algebra
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, for any Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
L one can construct its universal enveloping algebra U(L). This construction passes from the non-associative structure L to a (more familiar, and possibly easier to handle) unital associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
which captures the important properties of L.
Any associative algebra A over the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K becomes a Lie algebra over K with the Lie bracket:
- [a,b] = ab − ba.
That is, from an associative product, one can construct a Lie bracket by taking the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
with respect to that associative product. Denote this Lie algebra by AL.
Construction of the universal enveloping algebra attempts to reverse this process: to a given Lie algebra L over K, find the "most general" unital associative K-algebra A such that the Lie algebra AL contains L; this algebra A is U(L). The important constraint is to preserve the representation theory: the representations
Representation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
of L correspond in a one-to-one manner to the module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over U(L). In a typical context where L is acting by infinitesimal transformation
Infinitesimal transformation
In mathematics, an infinitesimal transformation is a limiting form of small transformation. For example one may talk about an infinitesimal rotation of a rigid body, in three-dimensional space. This is conventionally represented by a 3×3 skew-symmetric matrix A...
s, the elements of U(L) act like differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s, of all orders.
Motivation
An important topic in Lie algebras studies and probably the main source of theirappearance in applications is representation of the Lie algebra. A representation
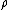 assigns to any element x
assigns to any element xof a Lie algebra a linear operator
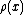 . The space of linear operators
. The space of linear operatorsis not only a Lie algebra, but also an associative algebra and so one can consider products
 . The main point to introduce the universal enveloping algebra is to study such products in various representations of a Lie algebra.
. The main point to introduce the universal enveloping algebra is to study such products in various representations of a Lie algebra.One obstacle can be immediately seen in a naive attempt to do this:
properties of products drastically depend on the representation, not only on the Lie algebra itself. For example for one representation we might have
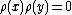 , while in another representation this product may not be zero.
, while in another representation this product may not be zero.Nevertheless it appears to be true that certain properties are universal for all representations, i.e. they hold true for all representations simultaneously. The universal enveloping algebra is a way to grasp all such properties and only them.
Universal property
Let X be any Lie algebra over K. Given a unital associative K-algebra U and a Lie algebra homomorphism- h: X → UL,
(notation as above) we say that U is the universal enveloping algebra of X if it satisfies the following universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: for any unital associative K-algebra A and Lie algebra homomorphism
- f: X → AL
there exists a unique unital algebra homomorphism
- g: U → A
such that
- f = gL h.
This is the universal property expressing that the functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
sending X to its universal enveloping algebra is left adjoint to the functor sending a unital associative algebra A to its Lie algebra AL.
Direct construction
From this universal property, one can prove that if a Lie algebra has a universal enveloping algebra, then this enveloping algebra is uniquely determined by L (up to a unique algebra isomorphism).By the following construction, which suggests itself on general grounds (for instance, as part of a pair of adjoint functors
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
), we establish that indeed every Lie algebra does have a universal enveloping algebra.
Starting with the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
T(L) on the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
underlying L, we take U(L) to be the quotient of T(L) made by imposing the relations
for all a and b in (the image in T(L) of) L, where the bracket on the RHS
Sides of an equation
In mathematics, LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. Each is solely a name for a term as part of an expression; and they are in practice interchangeable, since equality is symmetric...
means the given Lie algebra product, in L.
Formally, we define
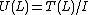
where I is the two-sided ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of T(L) generated by elements of the form
The natural map L → T(L) descends to a map h : L → U(L), and this is the Lie algebra homomorphism used in the universal property given above.
The analogous construction for Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
s is straightforward.
Examples in particular cases
If L is abelian (that is, the bracket is always 0), then U(L) is commutative; if a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
L has been chosen, then U(L) can be identified with the polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
algebra over K, with one variable per basis element.
If L is the Lie algebra corresponding to the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G, U(L) can be identified with the algebra of left-invariant differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s (of all orders) on G; with L lying inside it as the left-invariant vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s as first-order differential operators.
To relate the above two cases: if L is a vector space V as abelian Lie algebra, the left-invariant differential operators are the constant coefficient operators, which are indeed a polynomial algebra in the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of first order.
The center of U(L) is called Z(L) and consists of the left- and right- invariant differential operators; this in the case of G not commutative will often not be generated by first-order operators (see for example Casimir operator of a semi-simple Lie algebra).
Another characterisation in Lie group theory is of U(L) as the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
algebra of distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s supported only at the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
e of G.
The algebra of differential operators in n variables with polynomial coefficients may be obtained starting with the Lie algebra of the Heisenberg group. See Weyl algebra for this; one must take a quotient, so that the central elements of the Lie algebra act as prescribed scalars.
Further description of structure
The fundamental Poincaré–Birkhoff–Witt theoremPoincaré–Birkhoff–Witt theorem
In the theory of Lie algebras, the Poincaré–Birkhoff–Witt theorem is a result giving an explicit description of the universal enveloping algebra of a Lie algebra...
gives a precise description of U(L); the most important consequence is that L can be viewed as a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of U(L). More precisely: the canonical map h : L → U(L) is always injective. Furthermore, U(L) is generated as a unital associative algebra by L.
L acts on itself by the Lie algebra adjoint representation, and this action can be extended to a representation
Representation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
of L on U(L): L acts as an algebra of derivation
Derivation
Derivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
s on T(L), and this action respects the imposed relations, so it actually acts on U(L). (This is the purely infinitesimal way of looking at the invariant differential operators mentioned above.)
Under this representation, the elements of U(L) invariant under the action of L (i.e. such that any element of L acting on them gives zero) are called invariant elements. They are generated by the Casimir invariant
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
s.
As mentioned above, the construction of universal enveloping algebras is part of a pair of adjoint functors. U is a functor from the category of Lie algebras over K to the category of unital associative K-algebras. This functor is left adjoint to the functor which maps an algebra A to the Lie algebra AL. The universal enveloping algebra construction is not exactly inverse to the formation of AL: if we start with an associative algebra A, then U(AL) is not equal to A; it is much bigger.
The facts about representation theory mentioned earlier can be made precise as follows: the abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
of all representations
Representation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
of L is isomorphic
Isomorphism of categories
In category theory, two categories C and D are isomorphic if there exist functors F : C → D and G : D → C which are mutually inverse to each other, i.e. FG = 1D and GF = 1C. This means that both the objects and the morphisms of C and D stand in a one to one correspondence to each other...
to the abelian category of all left modules over U(L).
The construction of the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
for a given group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is in many ways analogous to constructing the universal enveloping algebra for a given Lie algebra. Both constructions are universal and translate representation theory into module theory. Furthermore, both group algebras and universal enveloping algebras carry natural comultiplications
Coalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
which turn them into Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s.