
Projection (linear algebra)
Encyclopedia
In linear algebra
and functional analysis
, a projection is a linear transformation
P from a vector space
to itself such that P2 = P. It leaves its image unchanged.
Though abstract, this definition of "projection" formalizes and generalizes the idea of graphical projection
. One can also consider the effect of a projection on a geometrical
object by examining the effect of the projection on point
s in the object.
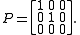
The action of this matrix on an arbitrary vector is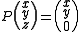
and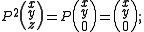
therefore P = P2, proving that P is indeed a projection.
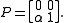
Via matrix multiplication
, one sees that
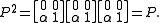
proving that P is indeed a projection.
The projection P is orthogonal if and only if = 0.
= 0.
As stated in the introduction, a projection P is a linear transformation that is idempotent, meaning that P2 = P.
Let W be an underlying vector space. Suppose the subspace
s U and V are the range and null space
of P respectively. Then we have these basic properties:
The range and kernel of a projection are complementary, as are P and Q = I − P. The operator Q is also a projection and the range and kernel of P become the kernel and range of Q and vice-versa.
We say P is a projection along V onto U (kernel/range) and Q is a projection along U onto V.
Decomposition of a vector space into direct sums is not unique in general. Therefore, given a subspace V, in general there are many projections whose range (or kernel) is V.
The spectrum
of a projection is contained in {0, 1}, as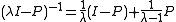 . Only 0 and 1 can be an eigenvalue of a projection, the corresponding eigenspaces are the range and kernel of the projection.
. Only 0 and 1 can be an eigenvalue of a projection, the corresponding eigenspaces are the range and kernel of the projection.
If a projection is nontrivial it has minimal polynomial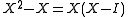 , which factors into distinct roots, and thus P is diagonalizable.
, which factors into distinct roots, and thus P is diagonalizable.
and its attendant notions (such as the self-adjointness of a linear operator) become available. An orthogonal projection is a projection for which the range U and the null space V are orthogonal subspaces
. A projection is orthogonal if and only if it is self-adjoint
, which means that, in the context of real vector spaces, the associated matrix is symmetric relative to an orthonormal basis: P = PT (for the complex case, the matrix is hermitian: P = (P*)T). Indeed, if x and y are vectors in the domain of the projection, then Px ∈ U and y − Py ∈ V, and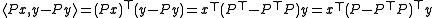
where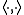 is the positive-definite scalar product, so Px and y − Py are orthogonal for all x and y if and only if P = PTP, which is equivalent to ( P = PT and P = P2 ).
is the positive-definite scalar product, so Px and y − Py are orthogonal for all x and y if and only if P = PTP, which is equivalent to ( P = PT and P = P2 ).
The simplest case is where the projection is an orthogonal projection onto a line. If u is a unit vector on the line, then the projection is given by
This operator leaves u invariant, and it annihilates all vectors orthogonal to u, proving that it is indeed the orthogonal projection onto the line containing u. A simple way to see this is to consider an arbitrary vector as the sum of a component on the line (i.e. the projected vector we seek) and another perpendicular to it,
as the sum of a component on the line (i.e. the projected vector we seek) and another perpendicular to it,  . Applying projection, we get
. Applying projection, we get 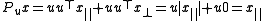 by the properties of the dot product
by the properties of the dot product
of parallel and perpendicular vectors.
This formula can be generalized to orthogonal projections on a subspace of arbitrary dimension. Let u1, ..., uk be an orthonormal basis
of the subspace U, and let A denote the n-by-k matrix whose columns are u1, ..., uk. Then the projection is given by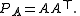
The matrix AT is the partial isometry
that vanishes on the orthogonal complement of U and A is the isometry that embeds U into the underlying vector space. The range of PA is therefore the final space of A. It is also clear that ATA is the identity operator on U.
The orthonormality condition can also be dropped. If u1, ..., uk is a (not necessarily orthonormal) basis, and A is the matrix with these vectors as columns, then the projection is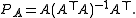
The matrix A still embeds U into the underlying vector space but is no longer an isometry in general. The matrix (ATA)−1 is a "normalizing factor" that recovers the norm. For example, the rank-1 operator uuT is not a projection if ||u|| ≠ 1. After dividing by uTu = ||u||2, we obtain the projection u(uTu)−1uT onto the subspace spanned by u.
If a matrix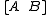 is non-singular and AT B = 0 (i.e., B is the null space
is non-singular and AT B = 0 (i.e., B is the null space
matrix of A), the following holds: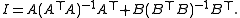
If the orthogonal condition is enhanced to AT W B = 0 with W being non-singular and symmetric, the following holds: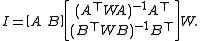
All these formulas also hold for complex inner product spaces, provided that the conjugate transpose
is used instead of the transpose.
), though not as frequently as orthogonal projections.
Oblique projections are defined by their range and null space. A formula for the matrix representing the projection with a given range and null space can be found as follows. Let the vectors u1, ..., uk form a basis for the range of the projection, and assemble these vectors in the n-by-k matrix A. The range and the null space are complementary spaces, so the null space has dimension n − k. It follows that the orthogonal complement of the null space has dimension k. Let v1, ..., vk form a basis for the orthogonal complement of the null space of the projection, and assemble these vectors in the matrix B. Then the projection is defined by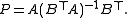
This expression generalizes the formula for orthogonal projections given above.
, since its minimal polynomial is x2 − x, which splits into distinct linear factors. Thus there exists a basis in which P has the form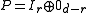
where r is the rank of P. Here Ir is the identity matrix of size r, and 0d−r is the zero matrix of size d − r. If the vector space is complex and equipped with an inner product, then there is an orthonormal basis in which the matrix of P is
 .
.
where . The integers k, s, m and the real numbers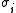 are uniquely determined. Note that . The factor corresponds to the maximal invariant subspace on which P acts as an orthogonal projection (so that P itself is orthogonal if and only if k = 0) and the σi-blocks correspond to the oblique components.
are uniquely determined. Note that . The factor corresponds to the maximal invariant subspace on which P acts as an orthogonal projection (so that P itself is orthogonal if and only if k = 0) and the σi-blocks correspond to the oblique components.
, analytic questions, irrelevant in the finite-dimensional case, need to be considered. Assume now X is a Banach space
.
Many of the algebraic notions discussed above survive the passage to this context. A given direct sum decomposition of X into complementary subspaces still specifies a projection, and vice versa. If X is the direct sum X = U ⊕ V, then the operator defined by P(u + v) = u is still a projection with range U and kernel V. It is also clear that P2 = P. Conversely, if P is projection on X, i.e. P2 = P, then it is easily verified that (I − P)2 = (I − P). In other words, (I − P) is also a projection. The relation I = P + (I − P) implies X is the direct sum Ran(P) ⊕ Ran(I − P).
However, in contrast to the finite-dimensional case, projections need not be continuous in general. If a subspace U of X is not closed in the norm topology, then projection onto U is not continuous. In other words, the range of a continuous projection P must be a closed subspace. Furthermore, the kernel of a continuous projection (in fact, a continuous linear operator in general) is closed. Thus a continuous projection P gives a decomposition of X into two complementary closed subspaces: X = Ran(P) ⊕ Ker(P) = Ran(P) ⊕ Ran(I − P).
The converse holds also, with an additional assumption. Suppose U is a closed subspace of X. If there exists a closed subspace V such that X = U ⊕ V, then the projection P with range U and kernel V is continuous. This follows from the closed graph theorem
. Suppose xn → x and Pxn → y. One needs to show Px = y. Since U is closed and {Pxn} ⊂ U, y lies in U, i.e. Py = y. Also, xn − Pxn = (I − P)xn → x − y. Because V is closed and {(I − P)xn} ⊂ V, we have x − y ∈ V, i.e. P(x − y) = Px − Py = Px − y = 0, which proves the claim.
The above argument makes use of the assumption that both U and V are closed. In general, given a closed subspace U, there need not exist a complementary closed subspace V, although for Hilbert space
s this can always be done by taking the orthogonal complement. For Banach spaces, a one-dimensional subspace always has a closed complementary subspace. This is an immediate consequence of Hahn–Banach theorem
. Let U be the linear span of u. By Hahn–Banach, there exists a bounded linear functional Φ such that φ(u) = 1. The operator P(x) = φ(x)u satisfies P2 = P, i.e. it is a projection. Boundedness of φ implies continuity of P and therefore Ker(P) = Ran(I − P) is a closed complementary subspace of U.
s for certain linear algebra problems:
As stated above, projections are a special case of idempotents. Analytically, orthogonal projections are non-commutative generalizations of characteristic function
s. Idempotents are used in classifying, for instance, semisimple algebra
s, while measure theory begins with considering characteristic functions of measurable sets. Therefore, as one can imagine, projections are very often encountered in the context operator algebra
s. In particular, a von Neumann algebra
is generated by its complete lattice
of projections.
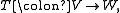 one can analogously ask for this map to be an isometry on the orthogonal complement of the kernel: that
one can analogously ask for this map to be an isometry on the orthogonal complement of the kernel: that 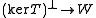 be an isometry; in particular it must be onto. The case of an orthogonal projection is when W is a subspace of V. In Riemannian geometry
be an isometry; in particular it must be onto. The case of an orthogonal projection is when W is a subspace of V. In Riemannian geometry
, this is used in the definition of a Riemannian submersion
.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a projection is a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
P from a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
to itself such that P2 = P. It leaves its image unchanged.
Though abstract, this definition of "projection" formalizes and generalizes the idea of graphical projection
Graphical projection
Graphical projection is a protocol by which an image of a three-dimensional object is projected onto a planar surface without the aid of mathematical calculation, used in technical drawing.- Overview :...
. One can also consider the effect of a projection on a geometrical
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
object by examining the effect of the projection on point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
s in the object.
Orthogonal projection
For example, the function which maps the point (x, y, z) in three-dimensional space R3 to the point (x, y, 0) is a projection onto the x-y plane. This function is represented by the matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
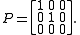
The action of this matrix on an arbitrary vector is
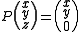
and
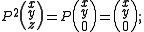
therefore P = P2, proving that P is indeed a projection.
Oblique projection
An example of a simple non-orthogonal (oblique) projection (for definition see below) is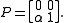
Via matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, one sees that
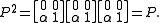
proving that P is indeed a projection.
The projection P is orthogonal if and only if
 = 0.
= 0.Classification
Assume the underlying vector space is finite dimensional (therefore issues such as continuity of a projection need not be considered).As stated in the introduction, a projection P is a linear transformation that is idempotent, meaning that P2 = P.
Let W be an underlying vector space. Suppose the subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
s U and V are the range and null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of P respectively. Then we have these basic properties:
- P is the identity operator I on U:
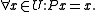
- We have a direct sum W = U ⊕ V. This means that every vector x may be decomposed uniquely in the manner x = u + v, where u is in U and v is in V. The decomposition is given by
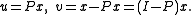
The range and kernel of a projection are complementary, as are P and Q = I − P. The operator Q is also a projection and the range and kernel of P become the kernel and range of Q and vice-versa.
We say P is a projection along V onto U (kernel/range) and Q is a projection along U onto V.
Decomposition of a vector space into direct sums is not unique in general. Therefore, given a subspace V, in general there are many projections whose range (or kernel) is V.
The spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of a projection is contained in {0, 1}, as
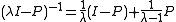 . Only 0 and 1 can be an eigenvalue of a projection, the corresponding eigenspaces are the range and kernel of the projection.
. Only 0 and 1 can be an eigenvalue of a projection, the corresponding eigenspaces are the range and kernel of the projection.If a projection is nontrivial it has minimal polynomial
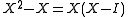 , which factors into distinct roots, and thus P is diagonalizable.
, which factors into distinct roots, and thus P is diagonalizable.Orthogonal projections
If the underlying vector space is endowed with an inner product, orthogonalityOrthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
and its attendant notions (such as the self-adjointness of a linear operator) become available. An orthogonal projection is a projection for which the range U and the null space V are orthogonal subspaces
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
. A projection is orthogonal if and only if it is self-adjoint
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
, which means that, in the context of real vector spaces, the associated matrix is symmetric relative to an orthonormal basis: P = PT (for the complex case, the matrix is hermitian: P = (P*)T). Indeed, if x and y are vectors in the domain of the projection, then Px ∈ U and y − Py ∈ V, and
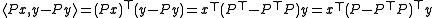
where
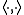 is the positive-definite scalar product, so Px and y − Py are orthogonal for all x and y if and only if P = PTP, which is equivalent to ( P = PT and P = P2 ).
is the positive-definite scalar product, so Px and y − Py are orthogonal for all x and y if and only if P = PTP, which is equivalent to ( P = PT and P = P2 ).The simplest case is where the projection is an orthogonal projection onto a line. If u is a unit vector on the line, then the projection is given by

This operator leaves u invariant, and it annihilates all vectors orthogonal to u, proving that it is indeed the orthogonal projection onto the line containing u. A simple way to see this is to consider an arbitrary vector
 as the sum of a component on the line (i.e. the projected vector we seek) and another perpendicular to it,
as the sum of a component on the line (i.e. the projected vector we seek) and another perpendicular to it,  . Applying projection, we get
. Applying projection, we get 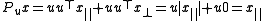 by the properties of the dot product
by the properties of the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of parallel and perpendicular vectors.
This formula can be generalized to orthogonal projections on a subspace of arbitrary dimension. Let u1, ..., uk be an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of the subspace U, and let A denote the n-by-k matrix whose columns are u1, ..., uk. Then the projection is given by
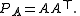
The matrix AT is the partial isometry
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
that vanishes on the orthogonal complement of U and A is the isometry that embeds U into the underlying vector space. The range of PA is therefore the final space of A. It is also clear that ATA is the identity operator on U.
The orthonormality condition can also be dropped. If u1, ..., uk is a (not necessarily orthonormal) basis, and A is the matrix with these vectors as columns, then the projection is
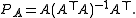
The matrix A still embeds U into the underlying vector space but is no longer an isometry in general. The matrix (ATA)−1 is a "normalizing factor" that recovers the norm. For example, the rank-1 operator uuT is not a projection if ||u|| ≠ 1. After dividing by uTu = ||u||2, we obtain the projection u(uTu)−1uT onto the subspace spanned by u.
If a matrix
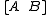 is non-singular and AT B = 0 (i.e., B is the null space
is non-singular and AT B = 0 (i.e., B is the null spaceNull space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
matrix of A), the following holds:
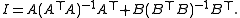
If the orthogonal condition is enhanced to AT W B = 0 with W being non-singular and symmetric, the following holds:
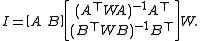
All these formulas also hold for complex inner product spaces, provided that the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
is used instead of the transpose.
Oblique projections
The term oblique projections is sometimes used to refer to non-orthogonal projections. These projections are also used to represent spatial figures in two-dimensional drawings (see oblique projectionOblique projection
Oblique projection is a simple type of graphical projection used for producing pictorial, two-dimensional images of three-dimensional objects.- Overview :Oblique projection is a type of parallel projection:...
), though not as frequently as orthogonal projections.
Oblique projections are defined by their range and null space. A formula for the matrix representing the projection with a given range and null space can be found as follows. Let the vectors u1, ..., uk form a basis for the range of the projection, and assemble these vectors in the n-by-k matrix A. The range and the null space are complementary spaces, so the null space has dimension n − k. It follows that the orthogonal complement of the null space has dimension k. Let v1, ..., vk form a basis for the orthogonal complement of the null space of the projection, and assemble these vectors in the matrix B. Then the projection is defined by
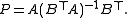
This expression generalizes the formula for orthogonal projections given above.
Canonical forms
Any projection on a vector space of dimension d over a field is a diagonalizable matrixDiagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
, since its minimal polynomial is x2 − x, which splits into distinct linear factors. Thus there exists a basis in which P has the form
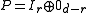
where r is the rank of P. Here Ir is the identity matrix of size r, and 0d−r is the zero matrix of size d − r. If the vector space is complex and equipped with an inner product, then there is an orthonormal basis in which the matrix of P is
 .
.where . The integers k, s, m and the real numbers
 are uniquely determined. Note that . The factor corresponds to the maximal invariant subspace on which P acts as an orthogonal projection (so that P itself is orthogonal if and only if k = 0) and the σi-blocks correspond to the oblique components.
are uniquely determined. Note that . The factor corresponds to the maximal invariant subspace on which P acts as an orthogonal projection (so that P itself is orthogonal if and only if k = 0) and the σi-blocks correspond to the oblique components.Projections on normed vector spaces
When the underlying vector space X is a (not necessarily finite-dimensional) normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
, analytic questions, irrelevant in the finite-dimensional case, need to be considered. Assume now X is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
Many of the algebraic notions discussed above survive the passage to this context. A given direct sum decomposition of X into complementary subspaces still specifies a projection, and vice versa. If X is the direct sum X = U ⊕ V, then the operator defined by P(u + v) = u is still a projection with range U and kernel V. It is also clear that P2 = P. Conversely, if P is projection on X, i.e. P2 = P, then it is easily verified that (I − P)2 = (I − P). In other words, (I − P) is also a projection. The relation I = P + (I − P) implies X is the direct sum Ran(P) ⊕ Ran(I − P).
However, in contrast to the finite-dimensional case, projections need not be continuous in general. If a subspace U of X is not closed in the norm topology, then projection onto U is not continuous. In other words, the range of a continuous projection P must be a closed subspace. Furthermore, the kernel of a continuous projection (in fact, a continuous linear operator in general) is closed. Thus a continuous projection P gives a decomposition of X into two complementary closed subspaces: X = Ran(P) ⊕ Ker(P) = Ran(P) ⊕ Ran(I − P).
The converse holds also, with an additional assumption. Suppose U is a closed subspace of X. If there exists a closed subspace V such that X = U ⊕ V, then the projection P with range U and kernel V is continuous. This follows from the closed graph theorem
Closed graph theorem
In mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
. Suppose xn → x and Pxn → y. One needs to show Px = y. Since U is closed and {Pxn} ⊂ U, y lies in U, i.e. Py = y. Also, xn − Pxn = (I − P)xn → x − y. Because V is closed and {(I − P)xn} ⊂ V, we have x − y ∈ V, i.e. P(x − y) = Px − Py = Px − y = 0, which proves the claim.
The above argument makes use of the assumption that both U and V are closed. In general, given a closed subspace U, there need not exist a complementary closed subspace V, although for Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s this can always be done by taking the orthogonal complement. For Banach spaces, a one-dimensional subspace always has a closed complementary subspace. This is an immediate consequence of Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
. Let U be the linear span of u. By Hahn–Banach, there exists a bounded linear functional Φ such that φ(u) = 1. The operator P(x) = φ(x)u satisfies P2 = P, i.e. it is a projection. Boundedness of φ implies continuity of P and therefore Ker(P) = Ran(I − P) is a closed complementary subspace of U.
Applications and further considerations
Projections (orthogonal and otherwise) play a major role in algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s for certain linear algebra problems:
- QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
(see Householder transformationHouseholder transformationIn linear algebra, a Householder transformation is a linear transformation that describes a reflection about a plane or hyperplane containing the origin. Householder transformations are widely used in numerical linear algebra, to perform QR decompositions and in the first step of the QR algorithm...
and Gram–Schmidt decomposition); - Singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
- Reduction to HessenbergHessenberg matrixIn linear algebra, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal...
form (the first step in many eigenvalue algorithmEigenvalue algorithmIn linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.-Characteristic polynomial:...
s). - Linear regressionLinear regressionIn statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
As stated above, projections are a special case of idempotents. Analytically, orthogonal projections are non-commutative generalizations of characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
s. Idempotents are used in classifying, for instance, semisimple algebra
Semisimple algebra
In ring theory, a semisimple algebra is an associative algebra which has trivial Jacobson radical...
s, while measure theory begins with considering characteristic functions of measurable sets. Therefore, as one can imagine, projections are very often encountered in the context operator algebra
Operator algebra
In functional analysis, an operator algebra is an algebra of continuous linear operators on a topological vector space with the multiplication given by the composition of mappings...
s. In particular, a von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
is generated by its complete lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of projections.
Generalizations
More generally, given a map between normed vector spaces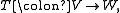 one can analogously ask for this map to be an isometry on the orthogonal complement of the kernel: that
one can analogously ask for this map to be an isometry on the orthogonal complement of the kernel: that 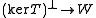 be an isometry; in particular it must be onto. The case of an orthogonal projection is when W is a subspace of V. In Riemannian geometry
be an isometry; in particular it must be onto. The case of an orthogonal projection is when W is a subspace of V. In Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, this is used in the definition of a Riemannian submersion
Riemannian submersion
In differential geometry, a branch of mathematics, a Riemannian submersion is a submersion from one Riemannian manifold to another that respects the metrics, meaning that it is an orthogonal projection on tangent spaces....
.
See also
- Centering matrixCentering matrixIn mathematics and multivariate statistics, the centering matrix is a symmetric and idempotent matrix, which when multiplied with a vector has the same effect as subtracting the mean of the components of the vector from every component.- Definition :...
, which is an example of a projection matrix. - Orthogonalization
- Invariant subspaceInvariant subspaceIn mathematics, an invariant subspace of a linear mappingfrom some vector space V to itself is a subspace W of V such that T is contained in W...
External links
- MIT Linear Algebra Lecture on Projection Matrices at Google Video, from MIT OpenCourseWare
- Planar Geometric Projections Tutorial - a simple-to-follow tutorial explaining the different types of planar geometric projections.

