
Tannaka-Krein duality
Encyclopedia
In mathematics
, Tannaka–Krein duality theory concerns the interaction of a compact
topological group
and its category of linear representations. Its natural extension to the non-Abelian
case is the Grothendieck duality theory.
It extends an important mathematical duality between compact and discrete commutative topological groups, known as Pontryagin duality
, to groups that are compact, but noncommutative. The theory is named for two men, the Soviet mathematician Mark Grigorievich Krein, and the Japanese Tadao Tannaka
. In contrast to the case of commutative groups considered by Lev Pontryagin, the notion dual to a noncommutative compact group
is not a group, but a category
Π(G) with some additional structures, formed by the finite-dimensional representations of G.
Duality theorems of Tannaka and Krein describe the converse passage from the category Π(G) back to the group G, allowing one to recover the group from its category of representations. Moreover, they in effect completely characterize all categories that can arise from a group in this fashion. Alexander Grothendieck
later showed that by a similar process, Tannaka duality can be extended to the case of algebraic group
s: see tannakian category
. Meanwhile, the original theory of Tannaka and Krein continued to be developed and refined by mathematical physicists
. A generalization of Tannaka–Krein theory provides the natural framework for studying representations of quantum groups, and is currently being extended to, quantum supergroups
, quantum groupoids and their dual quantum algebroids
.
 is its character group
is its character group
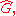 which consists of its one-dimensional unitary representation
which consists of its one-dimensional unitary representation
s. If we allow the group to be noncommutative, the most direct analogue of the character group is the set of equivalence classes of irreducible unitary representation
to be noncommutative, the most direct analogue of the character group is the set of equivalence classes of irreducible unitary representation
s of The analogue of the product of characters is the tensor product of representations. However, irreducible representations of
The analogue of the product of characters is the tensor product of representations. However, irreducible representations of  in general fail to form a group, because a tensor product of irreducible representations is not necessarily irreducible. It turns out that one needs to consider the set
in general fail to form a group, because a tensor product of irreducible representations is not necessarily irreducible. It turns out that one needs to consider the set 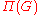 of all finite-dimensional representations, and treat it as monoidal category, where the product is the usual tensor product of representations, and the dual object is given by the operation of the contragredient representation. A representation of the category
of all finite-dimensional representations, and treat it as monoidal category, where the product is the usual tensor product of representations, and the dual object is given by the operation of the contragredient representation. A representation of the category  is a monoidal natural transformation
is a monoidal natural transformation
from the identity functor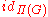 to itself. In other words, it is a non-zero function
to itself. In other words, it is a non-zero function  that associates with any
that associates with any 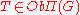 an endomorphism of the space of
an endomorphism of the space of  and satisfies the conditions of compatibility with tensor products,
and satisfies the conditions of compatibility with tensor products, 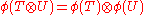 , and with arbitrary intertwining operators
, and with arbitrary intertwining operators 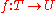 , namely,
, namely,  . The collection
. The collection 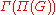 of all representations of the category
of all representations of the category 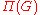 can be endowed with multiplication
can be endowed with multiplication 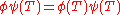 and topology, in which
and topology, in which  if it's true pointwise, i.e.
if it's true pointwise, i.e. 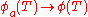 for all
for all 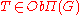 . It can be shown that the set
. It can be shown that the set 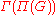 thus becomes a compact (topological) group.
thus becomes a compact (topological) group.
 from its category of representations
from its category of representations 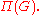
Let be a compact group and let
be a compact group and let 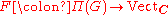 be the forgetful functor from finite-dimensional complex representations of G to complex finite-dimensional vector spaces. One puts a topology on the natural transformation
be the forgetful functor from finite-dimensional complex representations of G to complex finite-dimensional vector spaces. One puts a topology on the natural transformation
s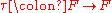 by setting it to be the coarsest topology possible such that each of the projections
by setting it to be the coarsest topology possible such that each of the projections  given by
given by  is a continuous function. We say that a natural transformation is tensor-preserving if it is the identity map on the trivial representation of G, and if it preserves tensor products in the sense that
is a continuous function. We say that a natural transformation is tensor-preserving if it is the identity map on the trivial representation of G, and if it preserves tensor products in the sense that 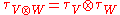 . We also say that
. We also say that  is self-conjugate if
is self-conjugate if  where the bar denotes complex conjugation. Then the set
where the bar denotes complex conjugation. Then the set 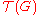 of all tensor-preserving, self-conjugate natural transformations of F is a closed set of End(F), which is in fact a (compact) group whenever G is a (compact) group. Every element x of G gives rise to a tensor-preserving self-conjugate natural transformation via multiplication by x on each representation, and hence one has a map
of all tensor-preserving, self-conjugate natural transformations of F is a closed set of End(F), which is in fact a (compact) group whenever G is a (compact) group. Every element x of G gives rise to a tensor-preserving self-conjugate natural transformation via multiplication by x on each representation, and hence one has a map 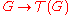 . Tannaka's theorem then says that this map is an isomorphism.
. Tannaka's theorem then says that this map is an isomorphism.
Krein's theorem answers the following question: which categories can arise as a dual object to a compact group?
Let be a category of finite-dimensional vector spaces, endowed with operations of tensor product and involution. The following conditions are necessary and sufficient in order for
be a category of finite-dimensional vector spaces, endowed with operations of tensor product and involution. The following conditions are necessary and sufficient in order for  to be a dual object to a compact group
to be a dual object to a compact group 
s in the work of Drinfel'd and Jimbo
. One of the main approaches to the study of a quantum group proceeds through its finite-dimensional representations, which form a category akin to the symmetric monoidal categories Π(G), but of more general type, braided monoidal category.
It turned out that a good duality theory of Tannaka–Krein type also exists in this case and plays an important role in the theory of quantum groups by providing a natural setting in which both the quantum groups and their representations can be studied. Shortly afterwards different examples of braided monoidal categories were found in rational conformal field theory
. Tannaka–Krein philosophy suggests that braided monoidal categories arising from conformal field theory can also be obtained from quantum groups, and in a series of papers, Kazhdan and Lusztig proved that it was indeed so. On the other hand, braided monoidal categories arising from certain quantum groups were applied by Reshetikhin and Turaev to construction of new invariants of knots.
, as a type of subcategory
of the category of Hilbert space
s. Such subcategories of compact group unitary representations on Hilbert spaces are:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Tannaka–Krein duality theory concerns the interaction of a compact
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and its category of linear representations. Its natural extension to the non-Abelian
Non-abelian
In theoretical physics, a non-abelian gauge transformation means a gauge transformation taking values in some group G, the elements of which do not obey the commutative law when they are multiplied. The original choice of G in the physics of electromagnetism was U, which is commutative.For a...
case is the Grothendieck duality theory.
It extends an important mathematical duality between compact and discrete commutative topological groups, known as Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
, to groups that are compact, but noncommutative. The theory is named for two men, the Soviet mathematician Mark Grigorievich Krein, and the Japanese Tadao Tannaka
Tadao Tannaka
was a Japanese mathematician. He is best known for developing the theory of Tannaka–Krein duality, which generalizes Pontryagin duality to noncommutative compact groups.Tannaka was born in Matsuyama, Ehime Prefecture...
. In contrast to the case of commutative groups considered by Lev Pontryagin, the notion dual to a noncommutative compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
is not a group, but a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
Π(G) with some additional structures, formed by the finite-dimensional representations of G.
Duality theorems of Tannaka and Krein describe the converse passage from the category Π(G) back to the group G, allowing one to recover the group from its category of representations. Moreover, they in effect completely characterize all categories that can arise from a group in this fashion. Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
later showed that by a similar process, Tannaka duality can be extended to the case of algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s: see tannakian category
Tannakian category
In mathematics, a tannakian category is a particular kind of monoidal category C, equipped with some extra structure relative to a given field K. The role of such categories C is to approximate, in some sense, the category of linear representations of an algebraic group G defined over K...
. Meanwhile, the original theory of Tannaka and Krein continued to be developed and refined by mathematical physicists
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
. A generalization of Tannaka–Krein theory provides the natural framework for studying representations of quantum groups, and is currently being extended to, quantum supergroups
Supergroup (physics)
The concept of supergroup is a generalization of that of group. In other words, every group is a supergroup but not every supergroup is a group. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them....
, quantum groupoids and their dual quantum algebroids
Lie algebroid
In mathematics, Lie algebroids serve the same role in the theory of Lie groupoids that Lie algebras serve in the theory of Lie groups: reducing global problems to infinitesimal ones...
.
The idea of Tannaka–Krein duality: category of representations of a group
In Pontryagin duality theory for locally compact commutative groups, the dual object to a group is its character group
is its character groupCharacter group
In mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory...
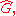 which consists of its one-dimensional unitary representation
which consists of its one-dimensional unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s. If we allow the group
 to be noncommutative, the most direct analogue of the character group is the set of equivalence classes of irreducible unitary representation
to be noncommutative, the most direct analogue of the character group is the set of equivalence classes of irreducible unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of
 The analogue of the product of characters is the tensor product of representations. However, irreducible representations of
The analogue of the product of characters is the tensor product of representations. However, irreducible representations of  in general fail to form a group, because a tensor product of irreducible representations is not necessarily irreducible. It turns out that one needs to consider the set
in general fail to form a group, because a tensor product of irreducible representations is not necessarily irreducible. It turns out that one needs to consider the set 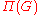 of all finite-dimensional representations, and treat it as monoidal category, where the product is the usual tensor product of representations, and the dual object is given by the operation of the contragredient representation. A representation of the category
of all finite-dimensional representations, and treat it as monoidal category, where the product is the usual tensor product of representations, and the dual object is given by the operation of the contragredient representation. A representation of the category  is a monoidal natural transformation
is a monoidal natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
from the identity functor
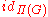 to itself. In other words, it is a non-zero function
to itself. In other words, it is a non-zero function  that associates with any
that associates with any 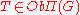 an endomorphism of the space of
an endomorphism of the space of  and satisfies the conditions of compatibility with tensor products,
and satisfies the conditions of compatibility with tensor products, 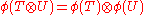 , and with arbitrary intertwining operators
, and with arbitrary intertwining operators 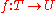 , namely,
, namely,  . The collection
. The collection 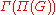 of all representations of the category
of all representations of the category 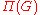 can be endowed with multiplication
can be endowed with multiplication 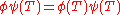 and topology, in which
and topology, in which  if it's true pointwise, i.e.
if it's true pointwise, i.e. 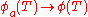 for all
for all 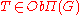 . It can be shown that the set
. It can be shown that the set 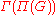 thus becomes a compact (topological) group.
thus becomes a compact (topological) group.Theorems of Tannaka and Krein
Tannaka's theorem provides a way to reconstruct the compact groupCompact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
 from its category of representations
from its category of representations 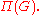
Let
 be a compact group and let
be a compact group and let 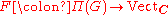 be the forgetful functor from finite-dimensional complex representations of G to complex finite-dimensional vector spaces. One puts a topology on the natural transformation
be the forgetful functor from finite-dimensional complex representations of G to complex finite-dimensional vector spaces. One puts a topology on the natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s
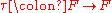 by setting it to be the coarsest topology possible such that each of the projections
by setting it to be the coarsest topology possible such that each of the projections  given by
given by  is a continuous function. We say that a natural transformation is tensor-preserving if it is the identity map on the trivial representation of G, and if it preserves tensor products in the sense that
is a continuous function. We say that a natural transformation is tensor-preserving if it is the identity map on the trivial representation of G, and if it preserves tensor products in the sense that 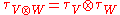 . We also say that
. We also say that  is self-conjugate if
is self-conjugate if  where the bar denotes complex conjugation. Then the set
where the bar denotes complex conjugation. Then the set 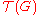 of all tensor-preserving, self-conjugate natural transformations of F is a closed set of End(F), which is in fact a (compact) group whenever G is a (compact) group. Every element x of G gives rise to a tensor-preserving self-conjugate natural transformation via multiplication by x on each representation, and hence one has a map
of all tensor-preserving, self-conjugate natural transformations of F is a closed set of End(F), which is in fact a (compact) group whenever G is a (compact) group. Every element x of G gives rise to a tensor-preserving self-conjugate natural transformation via multiplication by x on each representation, and hence one has a map 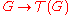 . Tannaka's theorem then says that this map is an isomorphism.
. Tannaka's theorem then says that this map is an isomorphism.Krein's theorem answers the following question: which categories can arise as a dual object to a compact group?
Let
 be a category of finite-dimensional vector spaces, endowed with operations of tensor product and involution. The following conditions are necessary and sufficient in order for
be a category of finite-dimensional vector spaces, endowed with operations of tensor product and involution. The following conditions are necessary and sufficient in order for  to be a dual object to a compact group
to be a dual object to a compact group 
- 1.There exists a unique up to isomorphism object with the property
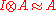 for all objects
for all objects  of
of 
- 2.Every object
 of
of  can be decomposed into a sum of minimal objects.
can be decomposed into a sum of minimal objects. - 3.If
 and
and  are two minimal objects then the space of homomorphisms
are two minimal objects then the space of homomorphisms  is either one-dimensional (when they are isomorphic) or is equal to zero. If all these conditions are satisfied then the category
is either one-dimensional (when they are isomorphic) or is equal to zero. If all these conditions are satisfied then the category  where
where  is the group of the representations of
is the group of the representations of 
Generalization
Interest to Tannaka–Krein duality theory was reawakened in the 1980s with the discovery of quantum groupQuantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s in the work of Drinfel'd and Jimbo
Michio Jimbo
is a Japanese mathematician, currently a professor at the University of Tokyo. He is a grandson of the linguist Kaku Jimbo.After graduating from the University of Tokyo in 1974, he studied under Mikio Sato at the Research Institute for Mathematical Sciences in Kyoto University...
. One of the main approaches to the study of a quantum group proceeds through its finite-dimensional representations, which form a category akin to the symmetric monoidal categories Π(G), but of more general type, braided monoidal category.
It turned out that a good duality theory of Tannaka–Krein type also exists in this case and plays an important role in the theory of quantum groups by providing a natural setting in which both the quantum groups and their representations can be studied. Shortly afterwards different examples of braided monoidal categories were found in rational conformal field theory
Rational conformal field theory
In theoretical physics, rational conformal field theory is a special type of conformal field theory with a finite number of conformal primaries. In these theories, all dimensions are rational numbers that can be computed from the consistency conditions of conformal field theory. The most famous...
. Tannaka–Krein philosophy suggests that braided monoidal categories arising from conformal field theory can also be obtained from quantum groups, and in a series of papers, Kazhdan and Lusztig proved that it was indeed so. On the other hand, braided monoidal categories arising from certain quantum groups were applied by Reshetikhin and Turaev to construction of new invariants of knots.
Doplicher–Roberts theorem
This result (due to Sergio Doplicher and John E. Roberts) characterises Rep(G) in terms of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, as a type of subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of the category of Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s. Such subcategories of compact group unitary representations on Hilbert spaces are:
- a strict symmetric monoidal C*-category with conjugates
- a subcategory having subobjectSubobjectIn category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s and direct sumDirect sumIn mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
s, such that the C*-algebra of endomorphisms of the monoidal unit contains only scalars.
External links
- UC Davis site with three articles on Tannaka Krein Duality
- Quantum Principal Bundles and Tannaka–Krein Duality by Mico Durdevic
- Quantum groups with invariant integrals by Alfons Van Daele (involves Tanaka–Krein)
- André Joyal and Ross Street, An introduction to Tannaka duality and quantum groups, in Part II of Category Theory, Proceedings, Como 1990, eds. A. Carboni, M. C. Pedicchio and G. Rosolini, Lectures Notes in Mathematics 1488, Springer, Berlin, 1991, 411–492.

