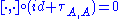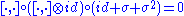
Lie superalgebra
Encyclopedia
In mathematics
, a Lie superalgebra is a generalisation of a Lie algebra
to include a Z2-grading
. Lie superalgebras are important in theoretical physics
where they are used to describe the mathematics of supersymmetry
. In most of these theories, the even elements of the superalgebra correspond to boson
s and odd elements to fermion
s (but this is not always true; for example, the BRST supersymmetry is the other way around).
, or superalgebra
, over a commutative ring
(typically R or C) whose product [·, ·], called the Lie superbracket or supercommutator, satisfies the two conditions (analogs of the usual Lie algebra
axioms, with grading):
Super skew-symmetry:
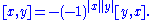
The super Jacobi identity:
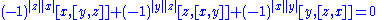
where x, y, and z are pure in the Z2-grading. Here, |x| denotes the degree of x (either 0 or 1). The degree of [x,y] is the sum of degree of x and y modulo 2.
One also sometimes adds the axioms for |x|=0 (if 2 is invertible this follows automatically) and
for |x|=0 (if 2 is invertible this follows automatically) and 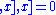 for |x|=1 (if 3 is invertible this follows automatically). When the ground ring is the integers or the Lie superalgebra is a free module, these conditions are equivalent to the condition that the Poincaré-Birkhoff-Witt theorem holds (and, in general, they are necessary conditions for the theorem to hold).
for |x|=1 (if 3 is invertible this follows automatically). When the ground ring is the integers or the Lie superalgebra is a free module, these conditions are equivalent to the condition that the Poincaré-Birkhoff-Witt theorem holds (and, in general, they are necessary conditions for the theorem to hold).
Just as for Lie algebras, the universal enveloping algebra
of the Lie superalgebra can be given a Hopf algebra
structure.
(say, graded by Z or N) that is anticommutative and Jacobi in the graded sense also has a grading (which is called "rolling up" the algebra into odd and even parts), but is not referred to as "super". See note at graded Lie algebra for discussion.
grading (which is called "rolling up" the algebra into odd and even parts), but is not referred to as "super". See note at graded Lie algebra for discussion.
One way of thinking about a Lie superalgebra is to consider its even and odd parts, L0 and L1 separately. Then, L0 is a Lie algebra, L1 is a linear representation
of L0, and there exists a symmetric L0-equivariant
linear map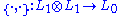 such that for all x,y and z in L1,
such that for all x,y and z in L1,
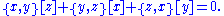
[x,y]*=[y*,x*] for all x and y in the Lie superalgebra. (Some authors prefer the convention [x,y]*=(−1)|x||y|[y*,x*]; changing * to −* switches between the two conventions.) Its universal enveloping algebra
would be an ordinary *-algebra
.
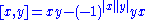
and then extending by linearity to all elements. The algebra A together with the supercommutator then becomes a Lie superalgebra.
The Whitehead product
on homotopy groups gives many examples of Lie superalgebras over the integers.
.
The basic classical compact Lie superalgebras (that are not Lie algebras) are: http://www.springerlink.com/content/f380116p6858n46n/
SU(m/n) These are the superunitary lie algebras which have invariants:
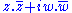
This gives two orthosymplectic (see below) invariants if we take the m z variables and n w variables to be non-commuative and we take the real and imaginary parts. Therefore we have
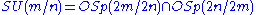
SU(n/n)/U(1) A special case of the superunitary lie algebras where we remove one U(1) generator to make the algebra simple.
OSp(m/2n) These are the Orthosymplectic groups. They have invariants given by:
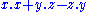
for m commutative variables (x) and n pairs of anti-commuative variables (y,z). They are important symmetries in supergravity
theories.
D(2/1; ) This is a set of superalgebras paramaterised by the variable
) This is a set of superalgebras paramaterised by the variable  . It has dimension 17 and is a sub-algebra of OSp(9|8). The even part of the group is O(3)xO(3)xO(3). So the invariants are:
. It has dimension 17 and is a sub-algebra of OSp(9|8). The even part of the group is O(3)xO(3)xO(3). So the invariants are:
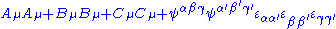

for particular constants .
.
F(4)
This exceptional lie superalgebra has dimension 40 and is a sub-algebra of OSp(24|16). The even part of the group is O(3)xSO(7) so three invariants are:
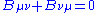


This group is related to the octonions by considering the 16 component spinors as two component octonion spinors and the gamma matrices acting on the upper indices as unit octonions. We then have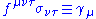 where f is the structure constants of octonion multiplication.
where f is the structure constants of octonion multiplication.
G(3)
This exceptional lie superalgebra has dimension 31 and is a sub-algebra of OSp(17|14). The even part of the group is O(3)xG2. The invariants are similar to the above (it being a subalgebra of the F(4)?) so the first invariant is:

There are also two so-called strange series called p(n) and q(n).
(m ≥ 2), SHO(m,m) (m ≥ 3), KO(m,m + 1), SKO(m,m + 1; β) (m ≥ 2), SHO∼(2m,2m), SKO∼(2m+1,2m + 3) and the 5 exceptional algebras:
The last two are particularly interesting (according to Kac) they have the standard model gauge group SU(3)xSU(2)xU(1) as their zero level algebra. Infinite dimensional (affine) lie superalgebras are important symmetries in superstring theory
.
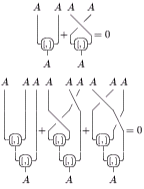
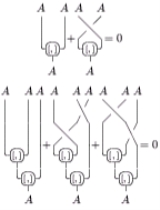
, a Lie superalgebra can be defined as a nonassociative superalgebra
whose product satisfies
where σ is the cyclic permutation braiding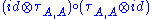 . In diagrammatic form:
. In diagrammatic form:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lie superalgebra is a generalisation of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
to include a Z2-grading
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
. Lie superalgebras are important in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
where they are used to describe the mathematics of supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. In most of these theories, the even elements of the superalgebra correspond to boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s and odd elements to fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s (but this is not always true; for example, the BRST supersymmetry is the other way around).
Definition
Formally, a Lie superalgebra is a (nonassociative) Z2-graded algebraGraded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
, or superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
, over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
(typically R or C) whose product [·, ·], called the Lie superbracket or supercommutator, satisfies the two conditions (analogs of the usual Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
axioms, with grading):
Super skew-symmetry:
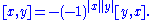
The super Jacobi identity:
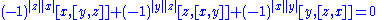
where x, y, and z are pure in the Z2-grading. Here, |x| denotes the degree of x (either 0 or 1). The degree of [x,y] is the sum of degree of x and y modulo 2.
One also sometimes adds the axioms
 for |x|=0 (if 2 is invertible this follows automatically) and
for |x|=0 (if 2 is invertible this follows automatically) and 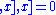 for |x|=1 (if 3 is invertible this follows automatically). When the ground ring is the integers or the Lie superalgebra is a free module, these conditions are equivalent to the condition that the Poincaré-Birkhoff-Witt theorem holds (and, in general, they are necessary conditions for the theorem to hold).
for |x|=1 (if 3 is invertible this follows automatically). When the ground ring is the integers or the Lie superalgebra is a free module, these conditions are equivalent to the condition that the Poincaré-Birkhoff-Witt theorem holds (and, in general, they are necessary conditions for the theorem to hold).Just as for Lie algebras, the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of the Lie superalgebra can be given a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
structure.
Distinction from graded Lie algebra
A graded Lie algebraGraded Lie algebra
In mathematics, a graded Lie algebra is a Lie algebra endowed with a gradation which is compatible with the Lie bracket. In other words, a graded Lie algebra is a Lie algebra which is also a nonassociative graded algebra under the bracket operation. A choice of Cartan decomposition endows any...
(say, graded by Z or N) that is anticommutative and Jacobi in the graded sense also has a
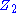 grading (which is called "rolling up" the algebra into odd and even parts), but is not referred to as "super". See note at graded Lie algebra for discussion.
grading (which is called "rolling up" the algebra into odd and even parts), but is not referred to as "super". See note at graded Lie algebra for discussion.Even and odd parts
Note that the even subalgebra of a Lie superalgebra forms a (normal) Lie algebra as all the signs disappear, and the superbracket becomes a normal Lie bracket.One way of thinking about a Lie superalgebra is to consider its even and odd parts, L0 and L1 separately. Then, L0 is a Lie algebra, L1 is a linear representation
Representation of a Lie algebra
In the mathematical field of representation theory, a Lie algebra representation or representation of a Lie algebra is a way of writing a Lie algebra as a set of matrices in such a way that the Lie bracket is given by the commutator.The notion is closely related to that of a representation of a...
of L0, and there exists a symmetric L0-equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
linear map
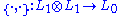 such that for all x,y and z in L1,
such that for all x,y and z in L1,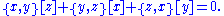
Involution
A * Lie superalgebra is a complex Lie superalgebra equipped with an involutive antilinear map from itself to itself which respects the Z2 grading and satisfies[x,y]*=[y*,x*] for all x and y in the Lie superalgebra. (Some authors prefer the convention [x,y]*=(−1)|x||y|[y*,x*]; changing * to −* switches between the two conventions.) Its universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
would be an ordinary *-algebra
Star-algebra
-*-ring:In mathematics, a *-ring is an associative ring with a map * : A → A which is an antiautomorphism and an involution.More precisely, * is required to satisfy the following properties:* ^* = x^* + y^** ^* = y^* x^** 1^* = 1...
.
Examples
Given any associative superalgebra A one can define the supercommutator on homogeneous elements by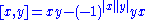
and then extending by linearity to all elements. The algebra A together with the supercommutator then becomes a Lie superalgebra.
The Whitehead product
Whitehead product
In mathematics, the Whitehead product is a graded quasi-Lie algebra structure on the homotopy groups of a space. It was defined by J. H. C. Whitehead in .- Definition :Given elements f \in \pi_k, g \in \pi_l, the Whitehead bracket...
on homotopy groups gives many examples of Lie superalgebras over the integers.
Classification
The simple complex finite dimensional Lie superalgebras were classified by Victor KacVictor Kac
Victor G. Kac is a Soviet and American mathematician at MIT, known for his work in representation theory. He discovered Kac–Moody algebras, and used the Weyl–Kac character formula for them to reprove the Macdonald identities...
.
The basic classical compact Lie superalgebras (that are not Lie algebras) are: http://www.springerlink.com/content/f380116p6858n46n/
SU(m/n) These are the superunitary lie algebras which have invariants:
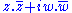
This gives two orthosymplectic (see below) invariants if we take the m z variables and n w variables to be non-commuative and we take the real and imaginary parts. Therefore we have
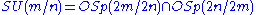
SU(n/n)/U(1) A special case of the superunitary lie algebras where we remove one U(1) generator to make the algebra simple.
OSp(m/2n) These are the Orthosymplectic groups. They have invariants given by:
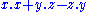
for m commutative variables (x) and n pairs of anti-commuative variables (y,z). They are important symmetries in supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
theories.
D(2/1;
 ) This is a set of superalgebras paramaterised by the variable
) This is a set of superalgebras paramaterised by the variable  . It has dimension 17 and is a sub-algebra of OSp(9|8). The even part of the group is O(3)xO(3)xO(3). So the invariants are:
. It has dimension 17 and is a sub-algebra of OSp(9|8). The even part of the group is O(3)xO(3)xO(3). So the invariants are: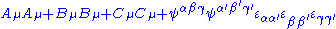

for particular constants
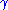 .
.F(4)
This exceptional lie superalgebra has dimension 40 and is a sub-algebra of OSp(24|16). The even part of the group is O(3)xSO(7) so three invariants are:
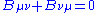


This group is related to the octonions by considering the 16 component spinors as two component octonion spinors and the gamma matrices acting on the upper indices as unit octonions. We then have
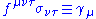 where f is the structure constants of octonion multiplication.
where f is the structure constants of octonion multiplication.G(3)
This exceptional lie superalgebra has dimension 31 and is a sub-algebra of OSp(17|14). The even part of the group is O(3)xG2. The invariants are similar to the above (it being a subalgebra of the F(4)?) so the first invariant is:

There are also two so-called strange series called p(n) and q(n).
Classification of Infinite Dimensional Simple Linearly Compact Lie Superalgebras
The classification consists of the 10 series W(m, n), S(m, n) ((m, n) ≠ (1, 1)), H(2m, n), K(2m+1, n) , HO(m,m)(m ≥ 2), SHO(m,m) (m ≥ 3), KO(m,m + 1), SKO(m,m + 1; β) (m ≥ 2), SHO∼(2m,2m), SKO∼(2m+1,2m + 3) and the 5 exceptional algebras:
-
- E(1,6), E(5,10), E(4,4), E(3,6), E(3,8)
The last two are particularly interesting (according to Kac) they have the standard model gauge group SU(3)xSU(2)xU(1) as their zero level algebra. Infinite dimensional (affine) lie superalgebras are important symmetries in superstring theory
Superstring theory
Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
.
Category-theoretic definition
In category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a Lie superalgebra can be defined as a nonassociative superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
whose product satisfies
where σ is the cyclic permutation braiding
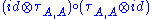 . In diagrammatic form:
. In diagrammatic form:See also
- Anyonic Lie algebra
- Grassmann algebra
- Representation of a Lie superalgebraRepresentation of a Lie superalgebraIn the mathematical field of representation theory, a representation of a Lie superalgebra is an action of Lie superalgebra L on a Z2-graded vector space V, such that if A and B are any two pure elements of L and X and Y are any two pure elements of V, then[X]=c_1 A[X] + c_2 B[X]\,A[c_1 X + c_2...
- SuperspaceSuperspace"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....
- SupergroupSupergroup (physics)The concept of supergroup is a generalization of that of group. In other words, every group is a supergroup but not every supergroup is a group. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them....