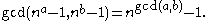Coprime
Encyclopedia
In number theory
, a branch of mathematics
, two integer
s a and b are said to be coprime (also spelled co-prime) or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor
being 1. In addition to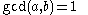 and
and  the notation a
the notation a 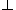 b is sometimes used to indicate that a and b are relatively prime.
b is sometimes used to indicate that a and b are relatively prime.
For example, 14 and 15 are coprime, being commonly divisible by only 1, but 14 and 21 are not, because they are both divisible by 7. The numbers 1 and −1 are coprime to every integer, and they are the only integers to be coprime with 0.
A fast way to determine whether two numbers are coprime is given by the Euclidean algorithm
.
The number of integers coprime to a positive integer n, between 1 and n, is given by Euler's totient function
(or Euler's phi function) φ(n).
As a consequence of the third point, if a and b are coprime and br ≡ bs (mod
a), then r ≡ s (mod a) (because we may "divide by b" when working modulo a). Furthermore, if b1 and b2 are both coprime with a, then so is their product b1b2 (modulo a it is a product of invertible elements, and therefore invertible); this also follows from the first point by Euclid's lemma
, which states that if a prime number p divides a product bc, then p divides at least one of the factors b, c.
As a consequence of the first point, if a and b are coprime, then so are any powers ak and bl.
If a and b are coprime and a divides the product bc, then a divides c. This can be viewed as a generalization of Euclid's lemma.
The two integers a and b are coprime if and only if the point with coordinates (a, b) in a Cartesian coordinate system
is "visible" from the origin (0,0), in the sense that there is no point with integer coordinates between the origin and (a, b). (See figure 1.)
In a sense that can be made precise, the probability
that two randomly chosen integers are coprime is 6/π2 (see pi
), which is about 61%. See below.
Two natural number
s a and b are coprime if and only if the numbers 2a − 1 and 2b − 1 are coprime. As a generalization of this, following easily from Euclidean algorithm
in base
n > 1:
, the numbers coprime to n, taken modulo
n, form a group
with multiplication as operation; it is written as (Z/nZ)× or Zn*.
R are called coprime (or comaximal) if A + B = R. This generalizes Bézout's identity
: with this definition, two principal ideal
s (a) and (b) in the ring of integers Z are coprime if and only if a and b are coprime.
If the ideals A and B of R are coprime, then AB = A∩B; furthermore, if C is a third ideal such that A contains BC, then A contains C. The Chinese remainder theorem
is an important statement about coprime ideals.
The concept of being relatively prime can also be extended to any finite set of integers S = {a1, a2, .... an} to mean that the greatest common divisor
of the elements of the set is 1. If every pair in a (finite or infinite) set of integers is relatively prime, then the set is called pairwise relatively prime.
Every pairwise relatively prime finite set is relatively prime; however, the converse is not true: {6, 10, 15} is relatively prime, but not pairwise relative prime (in fact, each pair of integers in the set has a non-trivial common factor).
 and
and 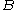 , it is reasonable to ask how likely it is that
, it is reasonable to ask how likely it is that 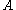 and
and 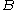 are coprime. In this determination, it is convenient to use the characterization that
are coprime. In this determination, it is convenient to use the characterization that  and
and 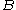 are coprime if and only if no prime number divides both of them (see Fundamental theorem of arithmetic
are coprime if and only if no prime number divides both of them (see Fundamental theorem of arithmetic
).
Intuitively, the probability that any number is divisible by a prime (or any integer),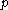 is
is  (for example, every 7th integer is divisible by 7.) Hence the probability that two numbers are both divisible by this prime is
(for example, every 7th integer is divisible by 7.) Hence the probability that two numbers are both divisible by this prime is 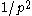 , and the probability that at least one of them is not is
, and the probability that at least one of them is not is 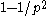 . Now, for distinct primes, these divisibility events are mutually independent. (This would not, in general, be true if they were not prime.) (For the case of two events, a number is divisible by p and q if and only if it is divisible by pq; the latter has probability 1/pq.) Thus the probability that two numbers are coprime is given by a product over all primes,
. Now, for distinct primes, these divisibility events are mutually independent. (This would not, in general, be true if they were not prime.) (For the case of two events, a number is divisible by p and q if and only if it is divisible by pq; the latter has probability 1/pq.) Thus the probability that two numbers are coprime is given by a product over all primes,
Here ζ refers to the Riemann zeta function, the identity relating the product over primes to ζ(2) is an example of an Euler product
, and the evaluation of ζ(2) as π2/6 is the Basel problem
, solved by Leonhard Euler
in 1735. In general, the probability of k randomly chosen integers being coprime is 1/ζ(k).
There is often confusion about what a "randomly chosen integer" is. One way of understanding this is to assume that the integers are chosen randomly between 1 and an integer N. Then, for each upper bound N, there is a probability PN that two randomly chosen numbers are coprime. This will never be exactly , but in the limit as
, but in the limit as  ,
, 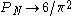 .
.
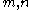 can be generated in a parent-3 children-9 grandchildren... family tree starting from
can be generated in a parent-3 children-9 grandchildren... family tree starting from 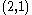 (for even-odd or odd-even pairs) or from
(for even-odd or odd-even pairs) or from 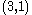 (for odd-odd pairs), with three branches from each node. The branches are generated as follows:
(for odd-odd pairs), with three branches from each node. The branches are generated as follows:
Branch 1: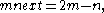 and
and 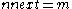
Branch 2: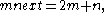 and
and 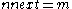
Branch 3: and
and 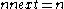
This family tree is exhaustive and non-redundant with no invalid members.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, two integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s a and b are said to be coprime (also spelled co-prime) or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
being 1. In addition to
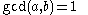 and
and  the notation a
the notation a 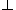 b is sometimes used to indicate that a and b are relatively prime.
b is sometimes used to indicate that a and b are relatively prime.For example, 14 and 15 are coprime, being commonly divisible by only 1, but 14 and 21 are not, because they are both divisible by 7. The numbers 1 and −1 are coprime to every integer, and they are the only integers to be coprime with 0.
A fast way to determine whether two numbers are coprime is given by the Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
.
The number of integers coprime to a positive integer n, between 1 and n, is given by Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
(or Euler's phi function) φ(n).
Properties
There are a number of conditions which are equivalent to a and b being coprime:- No prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
divides both a and b. - There exist integers x and y such that ax + by = 1 (see Bézout's identityBézout's identityIn number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
). - The integer b has a multiplicative inverse modulo a: there exists an integer y such that by ≡ 1 (mod a). In other words, b is a unitUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
Z/aZ of integers moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
a. - Every pair of congruence relationCongruence relationIn abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
s for an unknown integer x, of the form x ≡ k (mod a) and x ≡ l (mod b), has a solution, as stated by the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
; in fact the solutions are described by a single congruence relation modulo ab.
As a consequence of the third point, if a and b are coprime and br ≡ bs (mod
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
a), then r ≡ s (mod a) (because we may "divide by b" when working modulo a). Furthermore, if b1 and b2 are both coprime with a, then so is their product b1b2 (modulo a it is a product of invertible elements, and therefore invertible); this also follows from the first point by Euclid's lemma
Euclid's lemma
In mathematics, Euclid's lemma is an important lemma regarding divisibility and prime numbers. In its simplest form, the lemma states that a prime number that divides a product of two integers must divide one of the two integers...
, which states that if a prime number p divides a product bc, then p divides at least one of the factors b, c.
As a consequence of the first point, if a and b are coprime, then so are any powers ak and bl.
If a and b are coprime and a divides the product bc, then a divides c. This can be viewed as a generalization of Euclid's lemma.
The two integers a and b are coprime if and only if the point with coordinates (a, b) in a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is "visible" from the origin (0,0), in the sense that there is no point with integer coordinates between the origin and (a, b). (See figure 1.)
In a sense that can be made precise, the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that two randomly chosen integers are coprime is 6/π2 (see pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
), which is about 61%. See below.
Two natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s a and b are coprime if and only if the numbers 2a − 1 and 2b − 1 are coprime. As a generalization of this, following easily from Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
in base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
n > 1:
Cross notation, group
If n≥1 and is an integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, the numbers coprime to n, taken modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n, form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with multiplication as operation; it is written as (Z/nZ)× or Zn*.
Generalizations
Two ideals A and B in the commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R are called coprime (or comaximal) if A + B = R. This generalizes Bézout's identity
Bézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
: with this definition, two principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
s (a) and (b) in the ring of integers Z are coprime if and only if a and b are coprime.
If the ideals A and B of R are coprime, then AB = A∩B; furthermore, if C is a third ideal such that A contains BC, then A contains C. The Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
is an important statement about coprime ideals.
The concept of being relatively prime can also be extended to any finite set of integers S = {a1, a2, .... an} to mean that the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of the elements of the set is 1. If every pair in a (finite or infinite) set of integers is relatively prime, then the set is called pairwise relatively prime.
Every pairwise relatively prime finite set is relatively prime; however, the converse is not true: {6, 10, 15} is relatively prime, but not pairwise relative prime (in fact, each pair of integers in the set has a non-trivial common factor).
Probabilities
Given two randomly chosen integers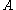 and
and 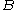 , it is reasonable to ask how likely it is that
, it is reasonable to ask how likely it is that 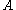 and
and 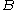 are coprime. In this determination, it is convenient to use the characterization that
are coprime. In this determination, it is convenient to use the characterization that  and
and 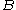 are coprime if and only if no prime number divides both of them (see Fundamental theorem of arithmetic
are coprime if and only if no prime number divides both of them (see Fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
).
Intuitively, the probability that any number is divisible by a prime (or any integer),
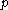 is
is  (for example, every 7th integer is divisible by 7.) Hence the probability that two numbers are both divisible by this prime is
(for example, every 7th integer is divisible by 7.) Hence the probability that two numbers are both divisible by this prime is 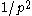 , and the probability that at least one of them is not is
, and the probability that at least one of them is not is 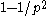 . Now, for distinct primes, these divisibility events are mutually independent. (This would not, in general, be true if they were not prime.) (For the case of two events, a number is divisible by p and q if and only if it is divisible by pq; the latter has probability 1/pq.) Thus the probability that two numbers are coprime is given by a product over all primes,
. Now, for distinct primes, these divisibility events are mutually independent. (This would not, in general, be true if they were not prime.) (For the case of two events, a number is divisible by p and q if and only if it is divisible by pq; the latter has probability 1/pq.) Thus the probability that two numbers are coprime is given by a product over all primes,Here ζ refers to the Riemann zeta function, the identity relating the product over primes to ζ(2) is an example of an Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
, and the evaluation of ζ(2) as π2/6 is the Basel problem
Basel problem
The Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate...
, solved by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in 1735. In general, the probability of k randomly chosen integers being coprime is 1/ζ(k).
There is often confusion about what a "randomly chosen integer" is. One way of understanding this is to assume that the integers are chosen randomly between 1 and an integer N. Then, for each upper bound N, there is a probability PN that two randomly chosen numbers are coprime. This will never be exactly
 , but in the limit as
, but in the limit as  ,
, 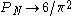 .
.Generating all coprime pairs
All pairs of coprime numbers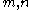 can be generated in a parent-3 children-9 grandchildren... family tree starting from
can be generated in a parent-3 children-9 grandchildren... family tree starting from 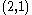 (for even-odd or odd-even pairs) or from
(for even-odd or odd-even pairs) or from 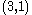 (for odd-odd pairs), with three branches from each node. The branches are generated as follows:
(for odd-odd pairs), with three branches from each node. The branches are generated as follows:Branch 1:
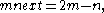 and
and 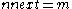
Branch 2:
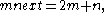 and
and 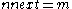
Branch 3:
 and
and 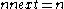
This family tree is exhaustive and non-redundant with no invalid members.