Cartan subalgebra
Encyclopedia
In mathematics
, a Cartan subalgebra, often abbreviated as CSA, is a nilpotent subalgebra
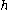of a Lie algebra
that is self-normalising (if 
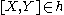for all 
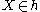, then 
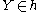). They were introduced by Élie Cartan
in his doctoral thesis.
Kac–Moody algebra
s and generalized Kac–Moody algebra
s also have Cartan subalgebras.
of characteristic 0 is abelian and
also has the following property of its adjoint representation: the weight
eigenspaces of
restricted
to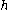
diagonalize the representation, and the eigenspace of the zero weight vector is 
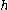. (So, the centralizer of 
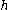coincides with 
.) The non-zero weights are called the roots
, and the corresponding eigenspaces are called root spaces
, and are all 1-dimensional.
If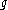
is a linear Lie algebra (a Lie subalgebra of the Lie algebra of endomorphisms of a finite-dimensional vector space V) over an algebraically closed field, then any Cartan subalgebra of 
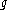is the centralizer of a maximal toral Lie subalgebra
of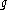
; that is, a subalgebra consisting entirely of elements which are diagonalizable as endomorphisms of V which is maximal in the sense that it is not properly included in any other such subalgebra. If 
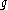is semisimple and the field has characteristic zero, then a maximal toral subalgebra is self-normalizing, and so is equal to the associated Cartan subalgebra. If in addition 
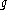is semisimple, then the adjoint representation
presents
as a linear Lie algebra, so that a subalgebra of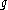 
is Cartan if and only if it is a maximal toral subalgebra. An advantage of this approach is that it is trivial to show the existence of such a subalgebra. In fact, if 
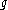has only nilpotent elements, then it is nilpotent (Engel's theorem), but then its Killing form
is identically zero, contradicting semisimplicity. Hence,
must have a nonzero semisimple element.
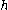then it is called splittable, and the pair 
is called a split Lie algebra; over an algebraically closed field every semisimple Lie algebra is splittable. Any two splitting Cartan algebras are conjugate, and they fulfill a similar function to Cartan algebras in semisimple Lie algebras over algebraically closed fields, so split semisimple Lie algebras (indeed, split reductive Lie algebras) share many properties with semisimple Lie algebras over algebraically closed fields.
Over a non-algebraically closed field not every semisimple Lie algebra is splittable, however.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Cartan subalgebra, often abbreviated as CSA, is a nilpotent subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
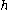of a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
that is self-normalising (if 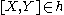for all 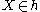, then 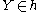). They were introduced by Élie CartanÉlie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
in his doctoral thesis.
Existence and uniqueness
Cartan subalgebras exist for finite dimensional Lie algebras whenever the base field is infinite. If the field is algebraically closed of characteristic 0 and the algebra is finite dimensional then all Cartan subalgebras are conjugate under automorphisms of the Lie algebra, and in particular are all isomorphic.Kac–Moody algebra
Kac–Moody algebra
In mathematics, a Kac–Moody algebra is a Lie algebra, usually infinite-dimensional, that can be defined by generators and relations through a generalized Cartan matrix...
s and generalized Kac–Moody algebra
Generalized Kac–Moody algebra
In mathematics, a generalized Kac–Moody algebra is a Lie algebra that is similar to aKac–Moody algebra, except that it is allowed to have imaginary simple roots.Generalized Kac–Moody algebras are also sometimes called GKM algebras,...
s also have Cartan subalgebras.
Properties
A Cartan subalgebra of a finite dimensional semisimple Lie algebra over an algebraically closed fieldAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
of characteristic 0 is abelian and
also has the following property of its adjoint representation: the weight
Weight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
eigenspaces of
restrictedRestricted representation
In mathematics, restriction is a fundamental construction in representation theory of groups. Restriction forms a representation of a subgroup from a representation of the whole group. Often the restricted representation is simpler to understand...
to
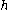diagonalize the representation, and the eigenspace of the zero weight vector is 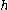. (So, the centralizer of 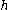coincides with .) The non-zero weights are called the rootsRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, and the corresponding eigenspaces are called root spaces
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, and are all 1-dimensional.
If
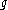is a linear Lie algebra (a Lie subalgebra of the Lie algebra of endomorphisms of a finite-dimensional vector space V) over an algebraically closed field, then any Cartan subalgebra of 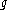is the centralizer of a maximal toral Lie subalgebraToral Lie algebra
In mathematics, a toral Lie algebra is a Lie subalgebra of a general linear Lie algebra all of whose elements are diagonalizable . Equivalently, a Lie algebra is toral if it contains no nonzero nilpotent elements...
of
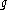; that is, a subalgebra consisting entirely of elements which are diagonalizable as endomorphisms of V which is maximal in the sense that it is not properly included in any other such subalgebra. If 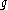is semisimple and the field has characteristic zero, then a maximal toral subalgebra is self-normalizing, and so is equal to the associated Cartan subalgebra. If in addition 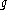is semisimple, then the adjoint representationAdjoint representation
In mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
presents
as a linear Lie algebra, so that a subalgebra of 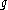is Cartan if and only if it is a maximal toral subalgebra. An advantage of this approach is that it is trivial to show the existence of such a subalgebra. In fact, if 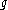has only nilpotent elements, then it is nilpotent (Engel's theorem), but then its Killing formKilling form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
is identically zero, contradicting semisimplicity. Hence,
must have a nonzero semisimple element.Examples
- Any nilpotent Lie algebra is its own Cartan subalgebra.
- A Cartan subalgebra of the Lie algebra of n×n matrices over a field is the algebra of all diagonal matrices.
- The Lie algebra sl2(R) of 2 by 2 matrices of trace 0 has two non-conjugate Cartan subalgebras.
- The dimension of a Cartan subalgebra is not in general the maximal dimension of an abelian subalgebra, even for complex simple Lie algebras. For example, the Lie algebra sl2n(C) of 2n by 2n matrices of trace 0 has a Cartan subalgebra of rank 2n−1 but has a maximal abelian subalgebra of dimension n2 consisting of all matrices of the form
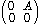with A any n by n matrix. One can directly see this abelian subalgebra is not a Cartan subalgebra, since it is contained in the nilpotent algebra of strictly upper triangular matrices (which is also not a Cartan subalgebra since it is normalized by diagonal matrices).
Splitting Cartan subalgebra
Over non-algebraically closed fields, not all Cartan subalgebras are conjugate. An important class are splitting Cartan subalgebras: if a Lie algebra admits a splitting Cartan subalgebra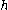 then it is called splittable, and the pair is called a split Lie algebra; over an algebraically closed field every semisimple Lie algebra is splittable. Any two splitting Cartan algebras are conjugate, and they fulfill a similar function to Cartan algebras in semisimple Lie algebras over algebraically closed fields, so split semisimple Lie algebras (indeed, split reductive Lie algebras) share many properties with semisimple Lie algebras over algebraically closed fields.Over a non-algebraically closed field not every semisimple Lie algebra is splittable, however.