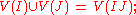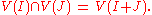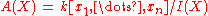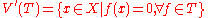Zariski topology
Encyclopedia
In algebraic geometry
, the Zariski topology is a particular topology
chosen for algebraic varieties
that reflects the algebraic nature of their definition. It is due to Oscar Zariski
and took a place of particular importance in the field around 1950. The more subtle étale topology
is a refinement of the Zariski topology discovered by Grothendieck in the 1960s that reflects the geometry more accurately.
which as sets are just n-dimensional vector spaces over k. The topology is defined by specifying its closed, rather than its open sets, and these are taken simply to be all the algebraic sets in 
That is, the closed sets are those of the form
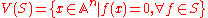
where S is any set of polynomials in n variables over k. It is a straightforward verification to show that:
It follows that finite unions and arbitrary intersections of the sets V(S) are also of this form, so that these sets form the closed sets of a topology (equivalently, their complements, denoted D(S) and called principal open sets, form the topology itself). This is the Zariski topology on
If X is an affine algebraic set (irreducible or not) then the Zariski topology on it is defined simply to be the subspace topology
induced by its inclusion into some
Equivalently, it can be checked that:
act as functions on X just as the elements of
act as functions on 
(these notations are not standard) is equal to the intersection with X of V(S).
This establishes that the above equation, clearly a generalization of the previous one, defines the Zariski topology on any affine variety.
is defined to be the set of equivalence classes of non-zero points in 
by identifying two points that differ by a scalar multiple in k. The elements of the polynomial ring 
are not functions on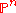 
because any point has many representatives that yield different values in a polynomial; however, the homogeneous polynomial
s do have well-defined zero or nonzero values on any projective point since the scalar multiple factors out of the polynomial. Therefore if S is any set of homogeneous polynomials we may reasonably speak of
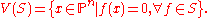
The same facts as above may be established for these sets, except that the word "ideal" must be replaced by the phrase "homogeneous ideal", so that the V(S), for sets S of homogeneous polynomials, define a topology on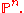
As above the complements of these sets are denoted D(S), or, if confusion is likely to result, D′(S).
The projective Zariski topology is defined for projective algebraic sets just as the affine one is defined for affine algebraic sets, by taking the subspace topology. Similarly, it may be shown that this topology is defined intrinsically by sets of elements of the projective coordinate ring, by the same formula as above.
for them consisting of particularly simple elements, namely the D(f) for individual polynomials (or for projective varieties, homogeneous polynomials) f. Indeed, that these form a basis follows from the formula for the intersection of two Zariski-closed sets given above (apply it repeatedly to the principal ideals generated by the generators of (S)). These are called distinguished or basic open sets.
By the Hilbert Basis Theorem and some elementary properties of Noetherian ring
s, every affine or projective coordinate ring is Noetherian. As a consequence, affine or projective spaces with the Zariski topology are Noetherian topological space
s, which implies that any subset of these spaces is compact
.
However, unless k is a finite field no variety is ever a Hausdorff space
. In the old topological literature "compact" was taken to include the Hausdorff property, and this convention is still honored in algebraic geometry; therefore compactness in the modern sense is called "quasicompactness" in algebraic geometry. However, since every point (a1, ..., an) is the zero set of the polynomials x1 - a1, ..., xn - an, points are closed and so every variety satisfies the T1 axiom
.
Every regular map of varieties is continuous in the Zariski topology. In fact, the Zariski topology is the weakest topology (with the fewest open sets) in which this is true and in which points are closed. This is easily verified by noting that the Zariski-closed sets are simply the intersections of the inverse images of 0 by the polynomial functions, considered as regular maps into
(the set of proper prime ideals) as its starting point. In this formulation, the Zariski-closed sets are taken to be the sets
where A is a fixed commutative ring and I is an ideal. To see the connection with the classical picture, note that for any set S of polynomials (over an algebraically closed field), it follows from Hilbert's Nullstellensatz
that the points of V(S) (in the old sense) are exactly the tuples (a1, ..., an) such that (x1 - a1, ..., xn - an) contains S; moreover, these are maximal ideals and by the "weak" Nullstellensatz, an ideal of any affine coordinate ring is maximal if and only if it is of this form. Thus, V(S) is "the same as" the maximal ideals containing S. Grothendieck's innovation in defining Spec was to replace maximal ideals with all prime ideals; in this formulation it is natural to simply generalize this observation to the definition of a closed set in the spectrum of a ring.
Another way, perhaps more similar to the original, to interpret the modern definition is to realize that the elements of A can actually be thought of as functions on the prime ideals of A; namely, as functions on Spec A. Simply, any prime ideal P has a corresponding residue field
, which is the field of fractions
of the quotient A/P, and any element of A has a reflection in this residue field. Furthermore, the elements that are actually in P are precisely those whose reflection vanishes. So if we think of the map, associated to any element a of A:
("evaluation of a"), which assigns to each point its reflection in the residue field there, as a function on Spec A (whose values, admittedly, lie in different fields at different points), then this function vanishes precisely at the points of V((a)). More generally, V(I) for any ideal I is the common set on which all the "functions" in I vanish, which is formally similar to the classical definition. In fact, they agree in the sense that when A is the ring of polynomials over some algebraically closed field k, the maximal ideals of A are (as discussed in the previous paragraph) identified with n-tuples of elements of k, their residue fields are just k, and the "evaluation" maps are actually evaluation of polynomials at the corresponding n-tuples. Since as shown above, the classical definition is essentially the modern definition with only maximal ideals considered, this shows that the interpretation of the modern definition as "zero sets of functions" agrees with the classical definition where they both make sense.
Just as Spec replaces affine varieties, the Proj construction
replaces projective varieties in modern algebraic geometry. Just as in the classical case, to move from the affine to the projective definition we need only replace "ideal" by "homogeneous ideal", though there is a complication involving the "irrelevant maximal ideal," which is discussed in the cited article.
s whose closures are strictly larger than themselves. The closed points correspond to maximal ideals of A. Note, however, that the spectrum and projective spectrum are still T0 spaces: given two points P, Q, which are prime ideals of A, at least one of them does not contain the other, say P. Then D(Q) contains P but, of course, not Q.
Just as in classical algebraic geometry, any spectrum or projective spectrum is compact, and if the ring in question is Noetherian then the space is a Noetherian space. However, these facts are counterintuitive: we do not normally expect open sets, other than connected components
, to be compact, and for affine varieties (for example, Euclidean space) we do not even expect the space itself to be compact. This is one instance of the geometric unsuitability of the Zariski topology. Grothendieck solved this problem by defining the notion of properness of a scheme
(actually, of a morphism of schemes), which recovers the intuitive idea of compactness: Proj is proper, but Spec is not.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Zariski topology is a particular topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
chosen for algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
that reflects the algebraic nature of their definition. It is due to Oscar Zariski
Oscar Zariski
Oscar Zariski was a Russian mathematician and one of the most influential algebraic geometers of the 20th century.-Education:...
and took a place of particular importance in the field around 1950. The more subtle étale topology
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
is a refinement of the Zariski topology discovered by Grothendieck in the 1960s that reflects the geometry more accurately.
The classical definition
In classical algebraic geometry (that is, the subject prior to the Grothendieck revolution of the late 1950s and 1960s) the Zariski topology was defined in the following way. Just as the subject itself was divided into the study of affine and projective varieties (see the Algebraic variety definitions) the Zariski topology is defined slightly differently for these two. We assume that we are working over a fixed, algebraically closed field k, which in classical geometry was almost always the complex numbers.Affine varieties
First we define the topology on affine spaces which as sets are just n-dimensional vector spaces over k. The topology is defined by specifying its closed, rather than its open sets, and these are taken simply to be all the algebraic sets in That is, the closed sets are those of the form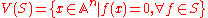where S is any set of polynomials in n variables over k. It is a straightforward verification to show that:
- V(S) = V((S)), where (S) is the idealIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by the elements of S; - For any two ideals of polynomials I, J, we have
-
It follows that finite unions and arbitrary intersections of the sets V(S) are also of this form, so that these sets form the closed sets of a topology (equivalently, their complements, denoted D(S) and called principal open sets, form the topology itself). This is the Zariski topology on
If X is an affine algebraic set (irreducible or not) then the Zariski topology on it is defined simply to be the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
induced by its inclusion into some
Equivalently, it can be checked that:- The elements of the affine coordinate ring
act as functions on X just as the elements of
act as functions on
- For any set of polynomials S, let T be the set of their images in A(X). Then the subset of X
(these notations are not standard) is equal to the intersection with X of V(S).
This establishes that the above equation, clearly a generalization of the previous one, defines the Zariski topology on any affine variety.
Projective varieties
Recall that n-dimensional projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
is defined to be the set of equivalence classes of non-zero points in by identifying two points that differ by a scalar multiple in k. The elements of the polynomial ring are not functions on 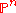because any point has many representatives that yield different values in a polynomial; however, the homogeneous polynomialHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s do have well-defined zero or nonzero values on any projective point since the scalar multiple factors out of the polynomial. Therefore if S is any set of homogeneous polynomials we may reasonably speak of
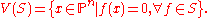
The same facts as above may be established for these sets, except that the word "ideal" must be replaced by the phrase "homogeneous ideal", so that the V(S), for sets S of homogeneous polynomials, define a topology on
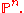As above the complements of these sets are denoted D(S), or, if confusion is likely to result, D′(S).The projective Zariski topology is defined for projective algebraic sets just as the affine one is defined for affine algebraic sets, by taking the subspace topology. Similarly, it may be shown that this topology is defined intrinsically by sets of elements of the projective coordinate ring, by the same formula as above.
Properties
A very useful fact about these topologies is that we may exhibit a basisBase (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for them consisting of particularly simple elements, namely the D(f) for individual polynomials (or for projective varieties, homogeneous polynomials) f. Indeed, that these form a basis follows from the formula for the intersection of two Zariski-closed sets given above (apply it repeatedly to the principal ideals generated by the generators of (S)). These are called distinguished or basic open sets.
By the Hilbert Basis Theorem and some elementary properties of Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s, every affine or projective coordinate ring is Noetherian. As a consequence, affine or projective spaces with the Zariski topology are Noetherian topological space
Noetherian topological space
In mathematics, a Noetherian topological space is a topological space in which closed subsets satisfy the descending chain condition. Equivalently, we could say that the open subsets satisfy the ascending chain condition, since they are the complements of the closed subsets...
s, which implies that any subset of these spaces is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
However, unless k is a finite field no variety is ever a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. In the old topological literature "compact" was taken to include the Hausdorff property, and this convention is still honored in algebraic geometry; therefore compactness in the modern sense is called "quasicompactness" in algebraic geometry. However, since every point (a1, ..., an) is the zero set of the polynomials x1 - a1, ..., xn - an, points are closed and so every variety satisfies the T1 axiom
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
.
Every regular map of varieties is continuous in the Zariski topology. In fact, the Zariski topology is the weakest topology (with the fewest open sets) in which this is true and in which points are closed. This is easily verified by noting that the Zariski-closed sets are simply the intersections of the inverse images of 0 by the polynomial functions, considered as regular maps into
The modern definition
Modern algebraic geometry takes the spectrum of a ringSpectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
(the set of proper prime ideals) as its starting point. In this formulation, the Zariski-closed sets are taken to be the sets
where A is a fixed commutative ring and I is an ideal. To see the connection with the classical picture, note that for any set S of polynomials (over an algebraically closed field), it follows from Hilbert's Nullstellensatz
Hilbert's Nullstellensatz
Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
that the points of V(S) (in the old sense) are exactly the tuples (a1, ..., an) such that (x1 - a1, ..., xn - an) contains S; moreover, these are maximal ideals and by the "weak" Nullstellensatz, an ideal of any affine coordinate ring is maximal if and only if it is of this form. Thus, V(S) is "the same as" the maximal ideals containing S. Grothendieck's innovation in defining Spec was to replace maximal ideals with all prime ideals; in this formulation it is natural to simply generalize this observation to the definition of a closed set in the spectrum of a ring.
Another way, perhaps more similar to the original, to interpret the modern definition is to realize that the elements of A can actually be thought of as functions on the prime ideals of A; namely, as functions on Spec A. Simply, any prime ideal P has a corresponding residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
, which is the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the quotient A/P, and any element of A has a reflection in this residue field. Furthermore, the elements that are actually in P are precisely those whose reflection vanishes. So if we think of the map, associated to any element a of A:
("evaluation of a"), which assigns to each point its reflection in the residue field there, as a function on Spec A (whose values, admittedly, lie in different fields at different points), then this function vanishes precisely at the points of V((a)). More generally, V(I) for any ideal I is the common set on which all the "functions" in I vanish, which is formally similar to the classical definition. In fact, they agree in the sense that when A is the ring of polynomials over some algebraically closed field k, the maximal ideals of A are (as discussed in the previous paragraph) identified with n-tuples of elements of k, their residue fields are just k, and the "evaluation" maps are actually evaluation of polynomials at the corresponding n-tuples. Since as shown above, the classical definition is essentially the modern definition with only maximal ideals considered, this shows that the interpretation of the modern definition as "zero sets of functions" agrees with the classical definition where they both make sense.
Just as Spec replaces affine varieties, the Proj construction
Proj construction
In algebraic geometry, Proj is a construction analogous to the spectrum-of-a-ring construction of affine schemes, which produces objects with the typical properties of projective spaces and projective varieties...
replaces projective varieties in modern algebraic geometry. Just as in the classical case, to move from the affine to the projective definition we need only replace "ideal" by "homogeneous ideal", though there is a complication involving the "irrelevant maximal ideal," which is discussed in the cited article.
Examples
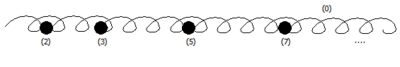
- Spec k, the spectrum of a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k is the topological space with one element. - Spec ℤ, the spectrum of the integers has a closed point for every prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p corresponding to the maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
(p) ⊂ ℤ, and one non-closed generic pointGeneric pointIn mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
(i.e., whose closure is the whole space) corresponding to the zero ideal (0). So the closed subsets of Spec ℤ are precisely finite unions of closed points and the whole space. - Spec k[t], the spectrum of the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k, which is also denoted
, the affine line: the polynomial ring is known to be a principal ideal domainPrincipal ideal domainIn abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
and the irreducible polynomialIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
s are the prime elementPrime elementIn abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
s of k[t]. If k is algebraically closed, for example the field of complex numbers, a non-constant polynomial is irreducible if and only if it is linear, of the form t − a, for some element a of k. So, the spectrum consists of one closed point for every element a of k and a generic point, corresponding to the zero ideal. If k is not algebraically closed, for example the field of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, the picture becomes more complicated because of the existence of non-linear irreducible polynomials. For example, the spectrum of ℝ[t] consists of closed points (x − a), for a in ℝ, (x2 + px + q) where p, q are in ℝ and with negative discriminantDiscriminantIn algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
p2 − 4q < 0, and finally a generic point (0). For any field, the closed subsets of Spec k[t] are finite unions of closed points, and the whole space. (This is clear from the above discussion for algebraically closed fields. The proof of the general case requires some commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, namely the fact, that the Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of k[t] is one — see Krull's principal ideal theoremKrull's principal ideal theoremIn commutative algebra, Krull's principal ideal theorem, named after Wolfgang Krull , gives a bound on the height of a principal ideal in a Noetherian ring...
).
Properties
The most dramatic change in the topology from the classical picture to the new is that points are no longer necessarily closed; by expanding the definition, Grothendieck introduced generic pointGeneric point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
s whose closures are strictly larger than themselves. The closed points correspond to maximal ideals of A. Note, however, that the spectrum and projective spectrum are still T0 spaces: given two points P, Q, which are prime ideals of A, at least one of them does not contain the other, say P. Then D(Q) contains P but, of course, not Q.
Just as in classical algebraic geometry, any spectrum or projective spectrum is compact, and if the ring in question is Noetherian then the space is a Noetherian space. However, these facts are counterintuitive: we do not normally expect open sets, other than connected components
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, to be compact, and for affine varieties (for example, Euclidean space) we do not even expect the space itself to be compact. This is one instance of the geometric unsuitability of the Zariski topology. Grothendieck solved this problem by defining the notion of properness of a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
(actually, of a morphism of schemes), which recovers the intuitive idea of compactness: Proj is proper, but Spec is not.