
Siegel modular form
Encyclopedia
In mathematics
, Siegel modular forms are a major type of automorphic form
. These stand in relation to the conventional elliptic modular form
s as abelian varieties do in relation to elliptic curve
s; the complex manifolds constructed as in the theory are basic models for what a moduli space
for abelian varieties (with some extra level structure) should be, as quotients of the Siegel upper half-space rather than the upper half-plane by discrete group
s.
The modular forms of the theory are holomorphic function
s on the set of symmetric n × n matrices with positive definite imaginary part; the forms must satisfy an automorphy condition. Siegel modular forms can be thought of as multivariable modular forms, i.e. as special functions of several complex variables
.
Siegel modular forms were first investigated by Carl Ludwig Siegel
in the 1930s for the purpose of studying quadratic form
s analytically. These primarily arise in various branches of number theory
, such as arithmetic geometry and elliptic cohomology
. Siegel modular forms have also been used in some areas of physics
, such as conformal field theory
.
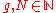 and define
and define
 ,
,
the Siegel upper half-space. Define the symplectic group
of level , denoted by
, denoted by

as
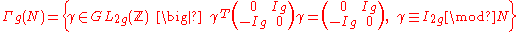 ,
,
where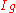 is the
is the 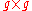 identity matrix
identity matrix
. Finally, let

be a rational representation
, where is a finite-dimensional complex vector space
is a finite-dimensional complex vector space
.
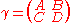
and

define the notation
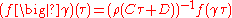 .
.
Then a holomorphic function

is a Siegel modular form of degree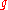 , weight
, weight 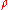 , and level
, and level  if
if
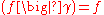 .
.
In the case that , we further require that
, we further require that  be holomorphic 'at infinity'. This assumption is not necessary for
be holomorphic 'at infinity'. This assumption is not necessary for  due to the Koecher principle, explained below. Denote the space of weight
due to the Koecher principle, explained below. Denote the space of weight 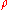 , degree
, degree 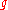 , and level
, and level  Siegel modular forms by
Siegel modular forms by
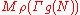 .
.
 is a Siegel modular form of weight
is a Siegel modular form of weight 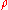 , level 1, and degree
, level 1, and degree  , then
, then  is bounded on subsets of
is bounded on subsets of  of the form
of the form

where . Corollary to this theorem is the fact that Siegel modular forms of degree
. Corollary to this theorem is the fact that Siegel modular forms of degree  have Fourier expansions and are thus holomorphic at infinity.
have Fourier expansions and are thus holomorphic at infinity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Siegel modular forms are a major type of automorphic form
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
. These stand in relation to the conventional elliptic modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s as abelian varieties do in relation to elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s; the complex manifolds constructed as in the theory are basic models for what a moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
for abelian varieties (with some extra level structure) should be, as quotients of the Siegel upper half-space rather than the upper half-plane by discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
s.
The modular forms of the theory are holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on the set of symmetric n × n matrices with positive definite imaginary part; the forms must satisfy an automorphy condition. Siegel modular forms can be thought of as multivariable modular forms, i.e. as special functions of several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
.
Siegel modular forms were first investigated by Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
in the 1930s for the purpose of studying quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s analytically. These primarily arise in various branches of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, such as arithmetic geometry and elliptic cohomology
Elliptic cohomology
In mathematics, elliptic cohomology is a cohomology theory in the sense of algebraic topology. It is related to elliptic curves and modular forms.-History and motivation:Historically, elliptic cohomology arose from the study of elliptic genera...
. Siegel modular forms have also been used in some areas of physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, such as conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
.
Preliminaries
Let and define
and define ,
,the Siegel upper half-space. Define the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
of level
 , denoted by
, denoted by
as
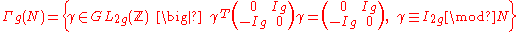 ,
,where
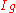 is the
is the 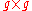 identity matrix
identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. Finally, let

be a rational representation
Rational representation
In mathematics, in the representation theory of algebraic groups, a linear representation of an algebraic group is said to be rational if, viewed as a map from the group to the general linear group, it is a rational map of algebraic varieties....
, where
 is a finite-dimensional complex vector space
is a finite-dimensional complex vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
.
Siegel modular form
Given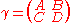
and

define the notation
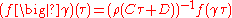 .
.Then a holomorphic function

is a Siegel modular form of degree
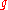 , weight
, weight 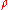 , and level
, and level  if
if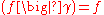 .
.In the case that
 , we further require that
, we further require that  be holomorphic 'at infinity'. This assumption is not necessary for
be holomorphic 'at infinity'. This assumption is not necessary for  due to the Koecher principle, explained below. Denote the space of weight
due to the Koecher principle, explained below. Denote the space of weight 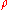 , degree
, degree 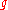 , and level
, and level  Siegel modular forms by
Siegel modular forms by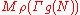 .
.Koecher principle
The theorem known as the Koecher principle states that if is a Siegel modular form of weight
is a Siegel modular form of weight 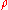 , level 1, and degree
, level 1, and degree  , then
, then  is bounded on subsets of
is bounded on subsets of 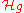 of the form
of the form
where
 . Corollary to this theorem is the fact that Siegel modular forms of degree
. Corollary to this theorem is the fact that Siegel modular forms of degree  have Fourier expansions and are thus holomorphic at infinity.
have Fourier expansions and are thus holomorphic at infinity.
