Projective representation
Encyclopedia
In the mathematical
field of representation theory
, a projective representation of a group
G on a vector space
V over a field
F is a group homomorphism
from G to the projective linear group
where GL(V,F) is the general linear group
of invertible linear transformations of V over F and F* here is the normal subgroup
consisting of multiplications of vectors in V by nonzero elements of F (that is, scalar multiples of the identity; scalar transformations).
of G on V and applying the quotient map
which is the quotient by the subgroup F∗ of scalar transformations (diagonal matrices with all diagonal entries equal). The interest for algebra is in the process in the other direction: given a projective representation, try to 'lift' it to a conventional linear representation.
In general, given a projective representation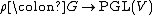
it cannot be lifted to a linear representation 
, and the obstruction
to this lifting can be understood via group homology, as described below. However, one can lift a projective representation of G to a linear representation of a different group C, which will be a central extension of G. To understand this, note that GL(V) → PGL(V) is a central extension of PGL, meaning that the kernel is central (in fact, is exactly the center of GL). One can pull back
the projective representation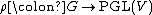
along the quotient map, obtaining a linear representation 
and C will be a central extension of G because it is a pullback of a central extension. Thus projective representations of G can be understood in terms of linear representations of (certain) central extensions of G. Notably, for G a perfect group
there is a single universal perfect central extension of G that can be used.
. Indeed, if one introduces for g in G a lifted element L(g) in lifting from PGL(V) back to GL(V), the lifts must satisfy
for some scalar c(g,h) in F∗. The 2-cocycle or Schur multiplier
c must satisfy the cocycle equation
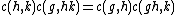
for all g, h, k in G. This c depends on the choice of the lift L, but a different choice of lift L' (g)= f(g) L(g) will result in a new cocycle
cohomologous to c. Thus L defines a unique class in H2(G, F∗), which need not be trivial. For example, in the case of the symmetric group
and alternating group, Schur proved that there is exactly one non-trivial class of Schur multiplier and completely determined all the corresponding irreducible representations.
It is shown, however, that this leads to an extension problem for G. If G is correctly extended we can speak of a linear representation of the extended group, which gives back the initial projective representation on factoring by F∗ and the extending subgroup. The solution is always a central extension. From Schur's lemma
, it follows that the irreducible representations of central extensions of G, and the irreducible projective representations of G, describe essentially the same questions of representation theory.
s leads one to consider true representations of their central extensions (see Group extension#Lie groups). In many cases of interest it suffices to consider representations of covering groups; for a connected Lie group G, this amounts to studying the representations of the Lie algebra of G. Notable cases of covering groups giving interesting projective representations:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, a projective representation of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from G to the projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
- PGL(V,F) = GL(V,F)/F∗
where GL(V,F) is the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of invertible linear transformations of V over F and F* here is the normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
consisting of multiplications of vectors in V by nonzero elements of F (that is, scalar multiples of the identity; scalar transformations).
Linear representations and projective representations
One way in which a projective representation can arise is by taking a linear group representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G on V and applying the quotient map
- GL(V, F) → PGL(V, F),
which is the quotient by the subgroup F∗ of scalar transformations (diagonal matrices with all diagonal entries equal). The interest for algebra is in the process in the other direction: given a projective representation, try to 'lift' it to a conventional linear representation.
In general, given a projective representation
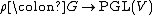it cannot be lifted to a linear representation , and the obstructionObstruction theory
In mathematics, obstruction theory is a name given to two different mathematical theories, both of which yield cohomological invariants.-In homotopy theory:...
to this lifting can be understood via group homology, as described below. However, one can lift a projective representation of G to a linear representation of a different group C, which will be a central extension of G. To understand this, note that GL(V) → PGL(V) is a central extension of PGL, meaning that the kernel is central (in fact, is exactly the center of GL). One can pull back
Pullback
Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
the projective representation
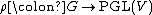along the quotient map, obtaining a linear representation and C will be a central extension of G because it is a pullback of a central extension. Thus projective representations of G can be understood in terms of linear representations of (certain) central extensions of G. Notably, for G a perfect groupPerfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
there is a single universal perfect central extension of G that can be used.
Group cohomology
The analysis of the lifting question involves group cohomologyGroup cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
. Indeed, if one introduces for g in G a lifted element L(g) in lifting from PGL(V) back to GL(V), the lifts must satisfy
- L(gh) = c(g,h)L(g)L(h)
for some scalar c(g,h) in F∗. The 2-cocycle or Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
c must satisfy the cocycle equation
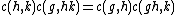
for all g, h, k in G. This c depends on the choice of the lift L, but a different choice of lift L' (g)= f(g) L(g) will result in a new cocycle
cohomologous to c. Thus L defines a unique class in H2(G, F∗), which need not be trivial. For example, in the case of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
and alternating group, Schur proved that there is exactly one non-trivial class of Schur multiplier and completely determined all the corresponding irreducible representations.
It is shown, however, that this leads to an extension problem for G. If G is correctly extended we can speak of a linear representation of the extended group, which gives back the initial projective representation on factoring by F∗ and the extending subgroup. The solution is always a central extension. From Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
, it follows that the irreducible representations of central extensions of G, and the irreducible projective representations of G, describe essentially the same questions of representation theory.
Projective representations of Lie groups
Studying projective representations of Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s leads one to consider true representations of their central extensions (see Group extension#Lie groups). In many cases of interest it suffices to consider representations of covering groups; for a connected Lie group G, this amounts to studying the representations of the Lie algebra of G. Notable cases of covering groups giving interesting projective representations:
- The special orthogonal group SO(n) is double covered by the Spin group Spin(n). In particular, the group SO(3) (the rotation group in 3 dimension) is double-covered by SU(2). This has important applications in quantum mechanics, as the study of representations of SU(2) leads naturally to the idea of spinSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
. - The orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n) is double covered by the Pin groupPin groupIn mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
s Pin±(n). - The symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(2n) is double covered by the metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
Mp(2n).