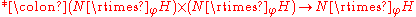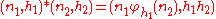Semidirect product
Encyclopedia
In mathematics
, specifically in the area of abstract algebra
known as group theory
, a semidirect product is a particular way in which a group
can be put together from two subgroup
s, one of which is a normal subgroup
. A semidirect product is a generalization of a direct product
. A semidirect product is a cartesian product
as a set, but with a particular multiplication operation.
e, N a normal subgroup
of G (i.e., N ◁ G) and H a subgroup
of G. The following statements are equivalent:
If one (and therefore all) of these statements hold, we say that G is a semidirect product of N and H, written
or that G splits over N;
one also says that G is a semidirect product of H acting on N, or even a semidirect product of H and N. In order to avoid ambiguities, it is advisable to specify which of the
two subgroups is normal.
Note that, as opposed to the case with the direct product
, a semidirect product of two groups is not, in general, unique; if G and G′ are two groups which both contain isomorphic copies of N as a normal subgroup and H as a subgroup, and both are a semidirect product of N and H, then it does not follow that G and G′ are isomorphic
. This remark leads to an extension problem, of describing the possibilities.
s of N. The map φ : H → Aut(N) defined by φ(h) = φh, where φh(n) = hnh-1 for all h in H and n in N, is a group homomorphism
. Together N, H and φ determine G up to
isomorphism, as we show now.
Given any two groups N and H (not necessarily subgroups of a given group) and a group homomorphism
: H → Aut(N), there is a new group 
(or simply 
), called the semidirect product of N and H with respect to 
, defined as follows.
This defines a group in which the identity element is (eN, eH) and the inverse of the element (n, h) is (
h–1(n–1), h–1). Pairs (n,eH) form a normal subgroup isomorphic to N, while pairs (eN, h) form a subgroup isomorphic to H. The full group is a semidirect product of those two subgroups in the sense given above.
Conversely, suppose that we are given a group G with a normal subgroup N and a subgroup H, such that every element g of G may be written uniquely in the form g=nh where n lies in N and h lies in H. Let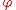
: H → Aut(N) be the homomorphism given by 
(h) =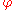 
h, where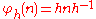
for all n in N and h in H.
Then G is isomorphic to the semidirect product
; the isomorphism sends the product nh to the tuple (n,h). In G, we have the multiplication rule
A version of the splitting lemma
for groups states that a group G is isomorphic to a semidirect product of the two groups N and H if and only if there exists a short exact sequence
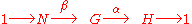
and a group homomorphism γ : H → G such that
, the identity map
on H. In this case,
: H → Aut(N) is given by 
(h) = 
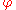h, where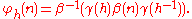
If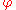
is the trivial homomorphism, sending every element of H to the identity automorphism of N, then 
is the direct product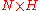 
.
D2n with 2n elements is isomorphic to a semidirect product of the cyclic group
s Cn and C2. Here, the non-identity element of C2 acts on Cn by inverting elements; this is an automorphism since Cn is abelian
. The presentation for this group is:
More generally, a semidirect product of any two cyclic groups
with generator 
and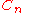 
with generator 
is given by a single relation 
with 
and 
coprime
, i.e. the presentation:
If
and 
are coprime, 
is a generator of 
and
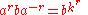, hence the presentation:
gives a group isomorphic to the previous one.
The fundamental group
of the Klein bottle
can be presented in the form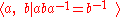
and is therefore a semidirect product of the group of integers,
, with itself.
The Euclidean group
of all rigid motions (isometries
) of the plane (maps f : R2 → R2 such that the Euclidean distance between x and y equals the distance between f(x) and f(y) for all x and y in R2) is isomorphic to a semidirect product of the abelian group R2 (which describes translations) and the group O(2) of orthogonal 2×2 matrices (which describes rotations and reflections which keep the origin fixed). n is a translation, h a rotation or reflection. Applying a translation and then a rotation or reflection corresponds to applying the rotation or reflection first and then a translation by the rotated or reflected translation vector (i.e. applying the conjugate
of the original translation). Every orthogonal matrix acts as an automorphism
on R2 by matrix multiplication.
The orthogonal group
O(n) of all orthogonal real n×n matrices (intuitively the set of all rotations and reflections of n-dimensional space which keep the origin fixed) is isomorphic to a semidirect product of the group SO(n) (consisting of all orthogonal matrices with determinant
1, intuitively the rotations of n-dimensional space) and C2. If we represent C2 as the multiplicative group of matrices {I, R}, where R is a reflection of n dimensional space which keeps the origin fixed (i.e. an orthogonal matrix with determinant –1 representing an involution), then φ : C2 → Aut(SO(n)) is given by φ(H)(N) = H N H–1 for all H in C2 and N in SO(n). In the non-trivial case ( H is not the identity) this means that φ(H) is conjugation of operations by the reflection (a rotation axis and the direction of rotation are replaced by their "mirror image").
of N and H.
The direct product of two groups N and H can be thought of as the outer semidirect product of N and H with respect to φ(h) = idN for all h in H.
Note that in a direct product, the order of the factors is not important, since N × H is isomorphic to H × N. This is not the case for semidirect products, as the two factors play different roles.
of groups is a generalization which, in its internal version, does not assume that either subgroup is normal. There is also a construction in ring theory
, the crossed product of rings. This is seen naturally as soon as one constructs a group ring
for a semidirect product of groups. There is also the semidirect sum of Lie algebras. Given a group action
on a topological space
, there is a corresponding crossed product which will in general be non-commutative even if the group is abelian. This kind of ring (see crossed product
for a related construction) can play the role of the space of orbits of the group action, in cases where that space cannot be approached by conventional topological techniques - for example in the work of Alain Connes
(cf. noncommutative geometry
).
There are also far-reaching generalisations in category theory
. They show how to construct fibred categories
from indexed categories. This is an abstract form of the outer semidirect product construction.
acts on a space 
it also acts on the fundamental groupoid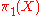 
of the space. The semidirect product 
is then relevant to finding the fundamental groupoid of the orbit space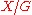 
. For full details see Chapter 11 of the book referenced below, and also some details in semidirect product in ncatlab
.
shows that every semidirect product is a direct product. Thus the existence of semidirect products reflects a failure of the category to be abelian.
or 
. However, some sources may use this symbol with the opposite meaning. In case the action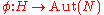 
should be made explicit, one also writes 
. One way of thinking about the 
symbol is as a combination of the symbol for normal subgroup (
) and the symbol for the product (
).
Unicode
lists four variants:
Here the Unicode description of the rtimes symbol says "right normal factor", in contrast to its usual meaning in mathematical practice.
In LaTeX
, the commands \rtimes and \ltimes produce the corresponding characters.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in the area of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a semidirect product is a particular way in which a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
can be put together from two subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s, one of which is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
. A semidirect product is a generalization of a direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
. A semidirect product is a cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
as a set, but with a particular multiplication operation.
Some equivalent definitions
Let G be a group with identity elementIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
e, N a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G (i.e., N ◁ G) and H a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G. The following statements are equivalent:
- G = NH and N ∩ H = {e}.
- G = HN and N ∩ H = {e}.
- Every element of G can be written as a unique product of an element of N and an element of H.
- Every element of G can be written as a unique product of an element of H and an element of N.
- The natural embedding H → G, composed with the natural projection G → G / N, yields an isomorphismGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
between H and the quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G / N. - There exists a homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
G → H which is the identity on H and whose kernelKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
is N.
If one (and therefore all) of these statements hold, we say that G is a semidirect product of N and H, written
or that G splits over N;one also says that G is a semidirect product of H acting on N, or even a semidirect product of H and N. In order to avoid ambiguities, it is advisable to specify which of the
two subgroups is normal.
Elementary facts and caveats
If G is the semidirect product of the normal subgroup N and the subgroup H, and both N and H are finite, then the order of G equals the product of the orders of N and H.Note that, as opposed to the case with the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
, a semidirect product of two groups is not, in general, unique; if G and G′ are two groups which both contain isomorphic copies of N as a normal subgroup and H as a subgroup, and both are a semidirect product of N and H, then it does not follow that G and G′ are isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
. This remark leads to an extension problem, of describing the possibilities.
Semidirect products and group homomorphisms
Let G be a semidirect product of the normal subgroup N and the subgroup H. Let Aut(N) denote the group of all automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of N. The map φ : H → Aut(N) defined by φ(h) = φh, where φh(n) = hnh-1 for all h in H and n in N, is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
. Together N, H and φ determine G up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism, as we show now.
Given any two groups N and H (not necessarily subgroups of a given group) and a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
: H → Aut(N), there is a new group (or simply ), called the semidirect product of N and H with respect to , defined as follows.
- As a set,
is the cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
N × H. - Multiplication of elements in
is determined by the homomorphism 
. The operation is
-
- defined by
- for n1, n2 in N and h1, h2 in H.
This defines a group in which the identity element is (eN, eH) and the inverse of the element (n, h) is (
h–1(n–1), h–1). Pairs (n,eH) form a normal subgroup isomorphic to N, while pairs (eN, h) form a subgroup isomorphic to H. The full group is a semidirect product of those two subgroups in the sense given above.Conversely, suppose that we are given a group G with a normal subgroup N and a subgroup H, such that every element g of G may be written uniquely in the form g=nh where n lies in N and h lies in H. Let
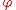: H → Aut(N) be the homomorphism given by (h) = 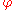h, where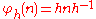for all n in N and h in H.
Then G is isomorphic to the semidirect product
; the isomorphism sends the product nh to the tuple (n,h). In G, we have the multiplication ruleA version of the splitting lemma
Splitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
for groups states that a group G is isomorphic to a semidirect product of the two groups N and H if and only if there exists a short exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
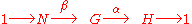
and a group homomorphism γ : H → G such that
, the identity mapIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on H. In this case,
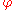: H → Aut(N) is given by 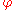(h) = h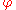, where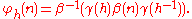If
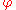is the trivial homomorphism, sending every element of H to the identity automorphism of N, then is the direct product 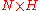.Examples
The dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
D2n with 2n elements is isomorphic to a semidirect product of the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s Cn and C2. Here, the non-identity element of C2 acts on Cn by inverting elements; this is an automorphism since Cn is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. The presentation for this group is:
More generally, a semidirect product of any two cyclic groups
with generator and 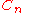with generator is given by a single relation with and coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
, i.e. the presentation:
If
and are coprime, is a generator of and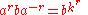, hence the presentation:gives a group isomorphic to the previous one.
The fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
can be presented in the form
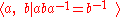
and is therefore a semidirect product of the group of integers,
, with itself.The Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
of all rigid motions (isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
) of the plane (maps f : R2 → R2 such that the Euclidean distance between x and y equals the distance between f(x) and f(y) for all x and y in R2) is isomorphic to a semidirect product of the abelian group R2 (which describes translations) and the group O(2) of orthogonal 2×2 matrices (which describes rotations and reflections which keep the origin fixed). n is a translation, h a rotation or reflection. Applying a translation and then a rotation or reflection corresponds to applying the rotation or reflection first and then a translation by the rotated or reflected translation vector (i.e. applying the conjugate
Conjugation of isometries in Euclidean space
In a group, the conjugate by g of h is ghg−1.-Translation:If h is a translation, then its conjugate by an isometry can be described as applying the isometry to the translation:...
of the original translation). Every orthogonal matrix acts as an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
on R2 by matrix multiplication.
The orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n) of all orthogonal real n×n matrices (intuitively the set of all rotations and reflections of n-dimensional space which keep the origin fixed) is isomorphic to a semidirect product of the group SO(n) (consisting of all orthogonal matrices with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1, intuitively the rotations of n-dimensional space) and C2. If we represent C2 as the multiplicative group of matrices {I, R}, where R is a reflection of n dimensional space which keeps the origin fixed (i.e. an orthogonal matrix with determinant –1 representing an involution), then φ : C2 → Aut(SO(n)) is given by φ(H)(N) = H N H–1 for all H in C2 and N in SO(n). In the non-trivial case ( H is not the identity) this means that φ(H) is conjugation of operations by the reflection (a rotation axis and the direction of rotation are replaced by their "mirror image").
Relation to direct products
Suppose G is a semidirect product of the normal subgroup N and the subgroup H. If H is also normal in G, or equivalently, if there exists a homomorphism G → N which is the identity on N, then G is the direct productDirect product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of N and H.
The direct product of two groups N and H can be thought of as the outer semidirect product of N and H with respect to φ(h) = idN for all h in H.
Note that in a direct product, the order of the factors is not important, since N × H is isomorphic to H × N. This is not the case for semidirect products, as the two factors play different roles.
Generalizations
The construction of semidirect products can be pushed much further. The Zappa-Szep productZappa-Szep product
In mathematics, especially group theory, the Zappa–Szép product describes a way in which a group can be constructed from two subgroups. It is a generalization of the direct and semidirect products...
of groups is a generalization which, in its internal version, does not assume that either subgroup is normal. There is also a construction in ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, the crossed product of rings. This is seen naturally as soon as one constructs a group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
for a semidirect product of groups. There is also the semidirect sum of Lie algebras. Given a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, there is a corresponding crossed product which will in general be non-commutative even if the group is abelian. This kind of ring (see crossed product
Crossed product
In mathematics, and more specifically in the theory of von Neumann algebras, a crossed productis a basic method of constructing a new von Neumann algebra froma von Neumann algebra acted on by a group. It is related to...
for a related construction) can play the role of the space of orbits of the group action, in cases where that space cannot be approached by conventional topological techniques - for example in the work of Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
(cf. noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
).
There are also far-reaching generalisations in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. They show how to construct fibred categories
Fibred category
Fibred categories are abstract entities in mathematics used to provide a general framework for descent theory. They formalise the various situations in geometry and algebra in which inverse images of objects such as vector bundles can be defined...
from indexed categories. This is an abstract form of the outer semidirect product construction.
Groupoids
Another generalisation is for groupoids. This occurs in topology because if a group acts on a space it also acts on the fundamental groupoid 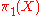of the space. The semidirect product is then relevant to finding the fundamental groupoid of the orbit space 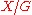. For full details see Chapter 11 of the book referenced below, and also some details in semidirect product in ncatlabNLab
nLab is a wiki-lab of a novel kind, for collaborative work on mathematics, physics, and philosophy, including original research, with a focus on category theory. The nLab espouses the n-point of view : that category theory and higher category theory provide a useful unifying viewpoint for...
.
Abelian categories
Non-trivial semidirect products do not arise in abelian categories, such as the category of modules. In this case, the splitting lemmaSplitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
shows that every semidirect product is a direct product. Thus the existence of semidirect products reflects a failure of the category to be abelian.
Notation
Usually the semidirect product of a group H acting on a group N (in most cases by conjugation as subgroups of a common group) is denoted by or . However, some sources may use this symbol with the opposite meaning. In case the action 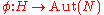should be made explicit, one also writes . One way of thinking about the symbol is as a combination of the symbol for normal subgroup () and the symbol for the product ().Unicode
Unicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
lists four variants:
| value | MathML | Unicode description | ||||
| ⋉ | U+22C9 | ltimes | LEFT NORMAL FACTOR SEMIDIRECT PRODUCT | |||
| ⋊ | U+22CA | rtimes | RIGHT NORMAL FACTOR SEMIDIRECT PRODUCT | |||
| ⋋ | U+22CB | lthree | LEFT SEMIDIRECT PRODUCT | |||
| ⋌ | U+22CC | rthree | RIGHT SEMIDIRECT PRODUCT |
Here the Unicode description of the rtimes symbol says "right normal factor", in contrast to its usual meaning in mathematical practice.
In LaTeX
LaTeX
LaTeX is a document markup language and document preparation system for the TeX typesetting program. Within the typesetting system, its name is styled as . The term LaTeX refers only to the language in which documents are written, not to the editor used to write those documents. In order to...
, the commands \rtimes and \ltimes produce the corresponding characters.