Invariant theory
Encyclopedia
Invariant theory is a branch of abstract algebra
dealing with actions
of groups
on algebraic varieties
from the point of view of their effect on functions. Classically, the theory dealt with the question of explicit description of polynomial functions that do not change, or are invariant, under the transformations from a given linear group.
Invariant theory of finite group
s has intimate connections with Galois theory
. One of the first major results was the main theorem on the symmetric function
s that described the invariants of the symmetric group
Sn acting on the polynomial ring
R[x1, …, xn] by permutation
s of the variables. More generally, the Chevalley–Shephard–Todd theorem
characterizes finite groups whose algebra of invariants is a polynomial ring. Modern research in invariant theory of finite groups emphasizes "effective" results, such as explicit bounds on the degrees of the generators. The case of positive characteristic
, ideologically close to modular representation theory
, is an area of active study, with links to algebraic topology
.
Invariant theory of infinite group
s is inextricably linked with the development of linear algebra
, especially, the theories of quadratic form
s and determinant
s. Another subject with strong mutual influence was projective geometry
, where invariant theory was expected to play a major role in organizing the material. One of the highlights of this relationship is the symbolic method
. Representation theory
of semisimple Lie groups has its roots in invariant theory.
David Hilbert
's work on the question of the finite generation of the algebra of invariants (1890) resulted in the creation of a new mathematical discipline, abstract algebra. A later paper of Hilbert (1893) dealt with the same questions in more constructive and geometric ways, but remained virtually unknown until David Mumford
brought these ideas back to life in the 1960s, in a considerably more general and modern form, in his geometric invariant theory
. In large measure due to the influence of Mumford, the subject of invariant theory is presently seen to encompass the theory of actions of linear algebraic group
s on affine and projective varieties. A distinct strand of invariant theory, going back to the classical constructive and combinatorial methods of the nineteenth century, has been developed by Gian-Carlo Rota
and his school. A prominent example of this circle of ideas is given by the theory of standard monomials.
of linear transformation
s. This was a major field of study in the latter part of the nineteenth century. Current theories relating to the symmetric group
and symmetric function
s, commutative algebra
, moduli space
s and the representations of Lie groups are rooted in this area.
In greater detail, given a finite-dimensional vector space
V of dimension n we can consider the symmetric algebra
S(Sr(V)) of the polynomials of degree r over V, and the action on it of GL(V). It is actually more accurate to consider the relative invariants of GL(V), or representations of SL(V), if we are going to speak of invariants: that is because a scalar multiple of the identity will act on a tensor of rank r in S(V) through the r-th power 'weight' of the scalar. The point is then to define the subalgebra of invariants I(Sr(V)) for the action. We are, in classical language, looking at invariants of n-ary r-ics, where n is the dimension of V. (This is not the same as finding invariants of GL(V) on S(V); this is an uninteresting problem as the only such invariants are constants.) The case that was most studied was invariants of binary forms where n=2.
Other work included that of Felix Klein
in computing the invariant rings of finite group actions on
(the binary polyhedral groups, classified by the ADE classification
); these are the coordinate rings of du Val singularities.
The work of David Hilbert
, proving that I(V) was finitely presented in many cases, almost put an end to classical invariant theory for several decades, though the classical epoch in the subject continued to the final publications of Alfred Young
, more than 50 years later. Explicit calculations for particular purposes have been known in modern times (for example Shioda, with the binary octavics).
ρ from R to RG with the properties
Hilbert constructed the Reynolds operator explicitly using Cayley's omega process Ω, though now it is more common to construct ρ indirectly as follows: for compact groups G, the Reynolds operator is given by taking the average over G, and non-compact reductive groups can be reduced to the case of compact groups using Weyl's unitarian trick
.
Given the Reynolds operator, Hilbert's theorem is proved as follows. The ring R is a polynomial ring so is graded by degrees, and the ideal I is defined to be the ideal generated by the homogeneous invariants of positive degrees. By Hilbert's basis theorem
the ideal I is finitely generated (as an ideal). Hence, I is finitely generated by finitely many invariants of G (because if we are given any - possibly infinite - subset S that generates a finitely generated ideal I, then I is already generated by some finite subset of S). Let i1,...,in be a finite set of invariants of G generating I (as an ideal). The key idea is to show that these generate the ring RG of invariants. Suppose that x is some homogeneous invariant of degree d>0. Then
for some aj in the ring R because x is in the ideal I. We can assume that aj is homogeneous of degree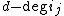
for every j (otherwise, we replace aj by its homogeneous component of degree 
; if we do this for every j, the equation x = a1i1 + ... + anin will remain valid). Now, applying the Reynolds operator to x = a1i1 + ... + anin gives
We are now going to show that x lies in the R-algebra generated by i1,...,in.
First, let us do this in the case when the elements ρ(ak) all have degree less than d. In this case, they are all in the R-algebra generated by i1,...,in (by our induction assumption). Therefore x is also in this R-algebra (since x = ρ(a1)i1 + ... + ρ(an)in).
In the general case, we cannot be sure that the elements ρ(ak) all have degree less than d. But we can replace each ρ(ak) by its homogeneous component of degree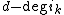
. As a result, these modified ρ(ak) are still G-invariants (because every homogeneous component of a G-invariant is a G-invariant) and have degree less than d (since 
). The equation x = ρ(a1)i1 + ... + ρ(an)in still holds for our modified ρ(ak), so we can again conclude that x lies in the R-algebra generated by i1,...,in.
Hence, by induction on the degree, all elements of RG are in the R-algebra generated by i1,...,in.
is due to David Mumford
, and emphasizes the construction of a quotient by the group action that should capture invariant information through its coordinate ring. It is a subtle theory, in that success is obtained by excluding some 'bad' orbits and identifying others with 'good' orbits. In a separate development the symbolic method of invariant theory, an apparently heuristic combinatorial notation, has been rehabilitated.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
dealing with actions
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
on algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
from the point of view of their effect on functions. Classically, the theory dealt with the question of explicit description of polynomial functions that do not change, or are invariant, under the transformations from a given linear group.
Invariant theory of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s has intimate connections with Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
. One of the first major results was the main theorem on the symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s that described the invariants of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn acting on the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
R[x1, …, xn] by permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of the variables. More generally, the Chevalley–Shephard–Todd theorem
Chevalley–Shephard–Todd theorem
In mathematics, the Chevalley–Shephard–Todd theorem in invariant theory of finite groups states that the ring of invariants of a finite group acting on a complex vector space is a polynomial ring if and only if the group is generated by pseudoreflections. In the case of subgroups of the complex...
characterizes finite groups whose algebra of invariants is a polynomial ring. Modern research in invariant theory of finite groups emphasizes "effective" results, such as explicit bounds on the degrees of the generators. The case of positive characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
, ideologically close to modular representation theory
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
, is an area of active study, with links to algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
.
Invariant theory of infinite group
Infinite group
In group theory, an area of mathematics, an infinite group is a group, of which the underlying set contains an infinite number of elements....
s is inextricably linked with the development of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, especially, the theories of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s and determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s. Another subject with strong mutual influence was projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, where invariant theory was expected to play a major role in organizing the material. One of the highlights of this relationship is the symbolic method
Symbolic method
In mathematics, the symbolic method in invariant theory is an algorithm developed by Arthur Cayley, , , and in the 19th century for computing invariants of algebraic forms...
. Representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of semisimple Lie groups has its roots in invariant theory.
David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's work on the question of the finite generation of the algebra of invariants (1890) resulted in the creation of a new mathematical discipline, abstract algebra. A later paper of Hilbert (1893) dealt with the same questions in more constructive and geometric ways, but remained virtually unknown until David Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
brought these ideas back to life in the 1960s, in a considerably more general and modern form, in his geometric invariant theory
Geometric invariant theory
In mathematics Geometric invariant theory is a method for constructing quotients by group actions in algebraic geometry, used to construct moduli spaces...
. In large measure due to the influence of Mumford, the subject of invariant theory is presently seen to encompass the theory of actions of linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
s on affine and projective varieties. A distinct strand of invariant theory, going back to the classical constructive and combinatorial methods of the nineteenth century, has been developed by Gian-Carlo Rota
Gian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
and his school. A prominent example of this circle of ideas is given by the theory of standard monomials.
The nineteenth century origins
Classically, the term "invariant theory" refers to the study of invariant algebraic forms (equivalently, symmetric tensors) for the actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s. This was a major field of study in the latter part of the nineteenth century. Current theories relating to the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
and symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s, commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
s and the representations of Lie groups are rooted in this area.
In greater detail, given a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V of dimension n we can consider the symmetric algebra
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
S(Sr(V)) of the polynomials of degree r over V, and the action on it of GL(V). It is actually more accurate to consider the relative invariants of GL(V), or representations of SL(V), if we are going to speak of invariants: that is because a scalar multiple of the identity will act on a tensor of rank r in S(V) through the r-th power 'weight' of the scalar. The point is then to define the subalgebra of invariants I(Sr(V)) for the action. We are, in classical language, looking at invariants of n-ary r-ics, where n is the dimension of V. (This is not the same as finding invariants of GL(V) on S(V); this is an uninteresting problem as the only such invariants are constants.) The case that was most studied was invariants of binary forms where n=2.
Other work included that of Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
in computing the invariant rings of finite group actions on
(the binary polyhedral groups, classified by the ADE classificationADE classification
In mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
); these are the coordinate rings of du Val singularities.
The work of David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, proving that I(V) was finitely presented in many cases, almost put an end to classical invariant theory for several decades, though the classical epoch in the subject continued to the final publications of Alfred Young
Alfred Young
Alfred Young, FRS was a British mathematician.He was born in Widnes, Lancashire, England and educated at Monkton Combe School in Somerset and Clare College, Cambridge, graduating BA as 10th Wrangler in 1895. He is known for his work in the area of group theory...
, more than 50 years later. Explicit calculations for particular purposes have been known in modern times (for example Shioda, with the binary octavics).
Hilbert's theorems
proved that if V is a finite dimensional representation of the complex algebraic group G= SLn(C) then the ring of invariants of G acting on the ring of polynomials R = S(V) is finitely generated. His proof used the Reynolds operatorReynolds operator
In fluid dynamics and invariant theory, a Reynolds operator is a mathematical operator given by averaging something over a group action, that satisfies a set of properties called Reynolds rules...
ρ from R to RG with the properties
- ρ(1)=1
- ρ(a+b) = ρ(a)+ρ(b)
- ρ(ab) = a ρ(b) whenever a is an invariant.
Hilbert constructed the Reynolds operator explicitly using Cayley's omega process Ω, though now it is more common to construct ρ indirectly as follows: for compact groups G, the Reynolds operator is given by taking the average over G, and non-compact reductive groups can be reduced to the case of compact groups using Weyl's unitarian trick
Unitarian trick
In mathematics, the unitarian trick is a device in the representation theory of Lie groups, introduced by for the special linear group and by Hermann Weyl for general semisimple groups. It applies to show that the representation theory of some group G is in a qualitative way controlled by that...
.
Given the Reynolds operator, Hilbert's theorem is proved as follows. The ring R is a polynomial ring so is graded by degrees, and the ideal I is defined to be the ideal generated by the homogeneous invariants of positive degrees. By Hilbert's basis theorem
Hilbert's basis theorem
In mathematics, specifically commutative algebra, Hilbert's basis theorem states that every ideal in the ring of multivariate polynomials over a Noetherian ring is finitely generated. This can be translated into algebraic geometry as follows: every algebraic set over a field can be described as the...
the ideal I is finitely generated (as an ideal). Hence, I is finitely generated by finitely many invariants of G (because if we are given any - possibly infinite - subset S that generates a finitely generated ideal I, then I is already generated by some finite subset of S). Let i1,...,in be a finite set of invariants of G generating I (as an ideal). The key idea is to show that these generate the ring RG of invariants. Suppose that x is some homogeneous invariant of degree d>0. Then
- x = a1i1 + ... + anin
for some aj in the ring R because x is in the ideal I. We can assume that aj is homogeneous of degree
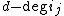for every j (otherwise, we replace aj by its homogeneous component of degree ; if we do this for every j, the equation x = a1i1 + ... + anin will remain valid). Now, applying the Reynolds operator to x = a1i1 + ... + anin gives
- x = ρ(a1)i1 + ... + ρ(an)in
We are now going to show that x lies in the R-algebra generated by i1,...,in.
First, let us do this in the case when the elements ρ(ak) all have degree less than d. In this case, they are all in the R-algebra generated by i1,...,in (by our induction assumption). Therefore x is also in this R-algebra (since x = ρ(a1)i1 + ... + ρ(an)in).
In the general case, we cannot be sure that the elements ρ(ak) all have degree less than d. But we can replace each ρ(ak) by its homogeneous component of degree
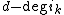. As a result, these modified ρ(ak) are still G-invariants (because every homogeneous component of a G-invariant is a G-invariant) and have degree less than d (since ). The equation x = ρ(a1)i1 + ... + ρ(an)in still holds for our modified ρ(ak), so we can again conclude that x lies in the R-algebra generated by i1,...,in.Hence, by induction on the degree, all elements of RG are in the R-algebra generated by i1,...,in.
Geometric invariant theory
The modern formulation of geometric invariant theoryGeometric invariant theory
In mathematics Geometric invariant theory is a method for constructing quotients by group actions in algebraic geometry, used to construct moduli spaces...
is due to David Mumford
David Mumford
David Bryant Mumford is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He won the Fields Medal and was a MacArthur Fellow. In 2010 he was awarded the National Medal of Science...
, and emphasizes the construction of a quotient by the group action that should capture invariant information through its coordinate ring. It is a subtle theory, in that success is obtained by excluding some 'bad' orbits and identifying others with 'good' orbits. In a separate development the symbolic method of invariant theory, an apparently heuristic combinatorial notation, has been rehabilitated.
See also
- invariant theory of finite groups
- Molien seriesMolien seriesIn mathematics, a Molien series is a generating function attached to a linear representation ρ of a group G on a finite-dimensional vector space V. It counts the homogeneous polynomials of a given total degree d that are invariants for G...
- invariant (mathematics)Invariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
External links
- H. Kraft, C. Procesi, Classical Invariant Theory, a Primer