Complete spatial randomness
Encyclopedia
Complete spatial randomness (CSR) describes a point process
whereby point events occur within a given study area in a completely random fashion. Such a process is often modeled using only one parameter, i.e. the density of points,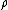
within the defined area. This is also called a spatial Poisson process
.
Data in the form of a set of points, irregularly distributed within a region of space, arise in many different contexts; examples include locations of trees in a forest, of nests of birds, of nuclei in tissue, of ill people in a population at risk. We call any such data-set a spatial point pattern and refer to the locations as events, to distinguish these from arbitrary points of the region in question.
with given mean count per uniform subdivision. The intensity of events does not vary over the plane. This implies that there are no interactions amongst the events. For example, the independence assumption would be violated if the existence of one event either encouraged or inhibited the occurrence of other events in the neighborhood. The study CSR is essential for the comparison of measured point data from experimental sources. As a statistical testing method, the test for CSR has many applications in the social sciences
and in astronomical examinations.
points within the area is therefore:
The first moment of which, the average number of points in the area, is simply
. This value is intuitive as it is the Poisson rate parameter.
The probability of locating the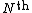
neighbor of any given point, at some radial distance 
is:
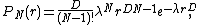
where
is the number of dimensions, and 
is the gamma function, which when its argument is integral, is simply the factorial
function.
is a density dependent parameter given by:
The expected value of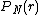
can be derived via the use of the gamma function
using statistical moments. The first moment is the distance between randomly distributed particles in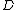
dimensions.
Point process
In statistics and probability theory, a point process is a type of random process for which any one realisation consists of a set of isolated points either in time or geographical space, or in even more general spaces...
whereby point events occur within a given study area in a completely random fashion. Such a process is often modeled using only one parameter, i.e. the density of points,
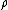within the defined area. This is also called a spatial Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
.
Data in the form of a set of points, irregularly distributed within a region of space, arise in many different contexts; examples include locations of trees in a forest, of nests of birds, of nuclei in tissue, of ill people in a population at risk. We call any such data-set a spatial point pattern and refer to the locations as events, to distinguish these from arbitrary points of the region in question.
Model
The hypothesis of complete spatial randomness for a spatial point pattern asserts that: the number of events in any region follows a Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with given mean count per uniform subdivision. The intensity of events does not vary over the plane. This implies that there are no interactions amongst the events. For example, the independence assumption would be violated if the existence of one event either encouraged or inhibited the occurrence of other events in the neighborhood. The study CSR is essential for the comparison of measured point data from experimental sources. As a statistical testing method, the test for CSR has many applications in the social sciences
Social sciences
Social science is the field of study concerned with society. "Social science" is commonly used as an umbrella term to refer to a plurality of fields outside of the natural sciences usually exclusive of the administrative or managerial sciences...
and in astronomical examinations.
Distribution
The probability of finding exactly points within the area is therefore:The first moment of which, the average number of points in the area, is simply
. This value is intuitive as it is the Poisson rate parameter.The probability of locating the
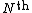neighbor of any given point, at some radial distance is: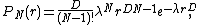where
is the number of dimensions, and is the gamma function, which when its argument is integral, is simply the factorialFactorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function.
is a density dependent parameter given by:The expected value of
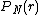can be derived via the use of the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
using statistical moments. The first moment is the distance between randomly distributed particles in
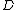dimensions.