Sesquilinear form
Encyclopedia
In mathematics
, a sesquilinear form on a complex vector space
V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix
sesqui- meaning "one and a half". Compare with a bilinear form, which is linear in both arguments; although many authors, especially when working solely in a complex
setting, refer to sesquilinear forms as bilinear forms.
A motivating example is the inner product on a complex vector space, which is not bilinear, but instead sesquilinear. See geometric motivation below.
bra-ket notation
in quantum mechanics
. The opposite convention is perhaps more common in mathematics but is not universal.
Specifically a map φ : V × V → C is sesquilinear if
for all x,y,z,w ∈ V and all a, b ∈ C.
A sesquilinear form can also be viewed as a complex bilinear map
where
is the complex conjugate vector space
to V. By the universal property of tensor product
s these are in one-to-one correspondence with (complex) linear maps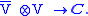
For a fixed z in V the map
is a linear functional
on V (i.e. an element of the dual space
V*). Likewise, the map
is a conjugate-linear functional on V.
Given any sesquilinear form φ on V we can define a second sesquilinear form ψ via the conjugate transpose
:
In general, ψ and φ will be different. If they are the same then φ is said to be Hermitian. If they are negatives of one another, then φ is said to be skew-Hermitian. Every sesquilinear form can be written as a sum of a Hermitian form and a skew-Hermitian form.
The norm associated to a sesquilinear form is invariant under multiplication by the complex circle (complex numbers of unit norm), while the norm associated to a bilinear form is equivariant
(with respect to squaring). Bilinear forms are algebraically more natural, while sesquilinear forms are geometrically more natural.
If B is a bilinear form on a complex vector space and
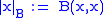is the associated norm,
then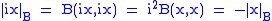
.
By contrast, if S is a sesquilinear form on a complex vector space and
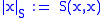is the associated norm,
then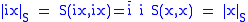
.
A Hermitian form (also called a symmetric sesquilinear form), is a sesquilinear form h : V × V → C such that
The standard Hermitian form on Cn is given by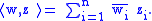
More generally, the inner product on any complex Hilbert space
is a Hermitian form.
A vector space with a Hermitian form (V,h) is called a Hermitian space.
If V is a finite-dimensional space, then relative to any basis
{ei} of V, a Hermitian form is represented by a Hermitian matrix H: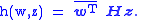
The components of H are given by Hij = h(ei, ej).
The quadratic form
associated to a Hermitian form
is always real
. Actually one can show that a sesquilinear form is Hermitian iff
the associated quadratic form is real for all z ∈ V.
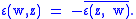
Every skew-Hermitian form can be written as i
times a Hermitian form.
If V is a finite-dimensional space, then relative to any basis
{ei} of V, a skew-Hermitian form is represented by a skew-Hermitian matrix
A: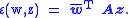
The quadratic form associated to a skew-Hermitian form
is always pure imaginary
.
Particularly in L-theory
, one also sees the term ε-symmetric form, where
, to refer to both symmetric and skew-symmetric forms.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a sesquilinear form on a complex vector space
Complex vector space
A complex vector space is a vector space over the complex numbers. It can also refer to:* a vector space over the real numbers with a linear complex structure...
V is a map V × V → C that is linear in one argument and antilinear in the other. The name originates from the numerical prefix
Numerical prefix
Number prefixes are prefixes derived from numbers or numerals. In English and other European languages, they are used to coin numerous series of words, such as unicycle – bicycle – tricycle, dyad – triad – decade, biped – quadruped, September – October – November – December, decimal – hexadecimal,...
sesqui- meaning "one and a half". Compare with a bilinear form, which is linear in both arguments; although many authors, especially when working solely in a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
setting, refer to sesquilinear forms as bilinear forms.
A motivating example is the inner product on a complex vector space, which is not bilinear, but instead sesquilinear. See geometric motivation below.
Definition and conventions
Conventions differ as to which argument should be linear. We take the first to be conjugate-linear and the second to be linear. This is the convention used by essentially all physicists and originates in Dirac'sPaul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. The opposite convention is perhaps more common in mathematics but is not universal.
Specifically a map φ : V × V → C is sesquilinear if
for all x,y,z,w ∈ V and all a, b ∈ C.
A sesquilinear form can also be viewed as a complex bilinear map
where
is the complex conjugate vector spaceComplex conjugate vector space
In mathematics, the complex conjugate of a complex vector space V\, is the complex vector space \overline V consisting of all formal complex conjugates of elements of V\,...
to V. By the universal property of tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s these are in one-to-one correspondence with (complex) linear maps
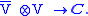
For a fixed z in V the map
is a linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on V (i.e. an element of the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
V*). Likewise, the map
is a conjugate-linear functional on V.Given any sesquilinear form φ on V we can define a second sesquilinear form ψ via the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
:
In general, ψ and φ will be different. If they are the same then φ is said to be Hermitian. If they are negatives of one another, then φ is said to be skew-Hermitian. Every sesquilinear form can be written as a sum of a Hermitian form and a skew-Hermitian form.
Geometric motivation
Bilinear forms are to squaring (z2), what sesquilinear forms are to Euclidean norm (|z|2 = z*z).The norm associated to a sesquilinear form is invariant under multiplication by the complex circle (complex numbers of unit norm), while the norm associated to a bilinear form is equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
(with respect to squaring). Bilinear forms are algebraically more natural, while sesquilinear forms are geometrically more natural.
If B is a bilinear form on a complex vector space and
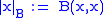is the associated norm,then
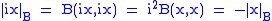.By contrast, if S is a sesquilinear form on a complex vector space and
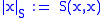is the associated norm,then
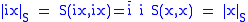.Hermitian form
- The term Hermitian form may also refer to a different concept than that explained below: it may refer to a certain differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on a Hermitian manifoldHermitian manifoldIn mathematics, a Hermitian manifold is the complex analog of a Riemannian manifold. Specifically, a Hermitian manifold is a complex manifold with a smoothly varying Hermitian inner product on each tangent space...
.
A Hermitian form (also called a symmetric sesquilinear form), is a sesquilinear form h : V × V → C such that
The standard Hermitian form on Cn is given by
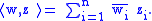
More generally, the inner product on any complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
is a Hermitian form.
A vector space with a Hermitian form (V,h) is called a Hermitian space.
If V is a finite-dimensional space, then relative to any basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
{ei} of V, a Hermitian form is represented by a Hermitian matrix H:
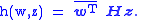
The components of H are given by Hij = h(ei, ej).
The quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
associated to a Hermitian form
- Q(z) = h(z,z)
is always real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Actually one can show that a sesquilinear form is Hermitian iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
the associated quadratic form is real for all z ∈ V.
Skew-Hermitian form
A skew-Hermitian form (also called an antisymmetric sesquilinear form), is a sesquilinear form ε : V × V → C such that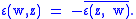Every skew-Hermitian form can be written as i
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
times a Hermitian form.
If V is a finite-dimensional space, then relative to any basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
{ei} of V, a skew-Hermitian form is represented by a skew-Hermitian matrix
Skew-Hermitian matrix
In linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
A:
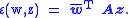
The quadratic form associated to a skew-Hermitian form
- Q(z) = ε(z,z)
is always pure imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
.
Generalization: over a *-ring
A sesquilinear form and a Hermitian form can be defined over any *-ring, and the examples of symmetric bilinear forms, skew-symmetric bilinear forms, Hermitian forms, and skew-Hermitian forms, are all Hermitian forms for various involutions.Particularly in L-theory
L-theory
Algebraic L-theory is the K-theory of quadratic forms; the term was coined by C. T. C. Wall,with L being used as the letter after K. Algebraic L-theory, also known as 'hermitian K-theory',is important in surgery theory.-Definition:...
, one also sees the term ε-symmetric form, where
, to refer to both symmetric and skew-symmetric forms.