
Topological group
Encyclopedia
In mathematics
, a topological group is a group
G together with a topology
on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a topological structure. Thus, one may perform algebraic operations, because of the group structure, and one may talk about continuous functions, because of the topology.
Topological groups, along with continuous group actions, are used to study continuous symmetries
, which have many applications, for example in physics.
and group
such that the group operations of product: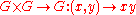
and taking inverses: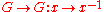
are continuous functions. Here, G × G is viewed as a topological space by using the product topology
.
Although we do not do so here, many authors require that the topology on G be Hausdorff
. The reasons, and some equivalent conditions, are discussed below. In the end, this is not a serious restriction—any topological group can be made Hausdorff in a canonical fashion.
In the language of category theory
, topological groups can be defined concisely as group object
s in the category of topological spaces
, in the same way that ordinary groups are group objects in the category of sets
.
between two topological groups G and H is just a continuous group homomorphism
G H. An isomorphism
H. An isomorphism
of topological groups is a group isomorphism
which is also a homeomorphism
of the underlying topological spaces. This is stronger than simply requiring a continuous group isomorphism—the inverse must also be continuous. There are examples of topological groups which are isomorphic as ordinary groups but not as topological groups. Indeed, any nondiscrete topological group is also a topological group when considered with the discrete topology. The underlying groups
are the same, but as topological groups there is not an isomorphism.
Topological groups, together with their homomorphisms, form a category
.
s. In this sense, the theory of topological groups subsumes that of ordinary groups.
The real number
s R, together with addition as operation and its usual topology, form a topological group. More generally, Euclidean n-space
Rn with addition and standard topology is a topological group. More generally yet, the additive groups of all topological vector space
s, such as Banach space
s or Hilbert space
s, are topological groups.
The above examples are all abelian
. Examples of non-abelian topological groups are given by the classical group
s. For instance, the general linear group
GL(n,R) of all invertible n-by-n matrices
with real entries can be viewed as a topological group with the topology defined by viewing GL(n,R) as a subset of Euclidean space Rn×n.
An example of a topological group which is not a Lie group
is given by the rational number
s Q with the topology inherited from R. This is a countable space and it does not have the discrete topology. For a nonabelian example, consider the subgroup of rotations of R3 generated by two rotations by irrational multiples of 2π about different axes.
In every Banach algebra
with multiplicative identity, the set of invertible elements forms a topological group under multiplication.
(i.e. the connected component
containing the identity element) is a closed
normal subgroup
. This is because if C is the identity component, a*C is the component of G (the group) containing a. In fact, the collection of all left cosets (or right cosets) of C in G is equal to the collection of all components of G. Therefore, the quotient topology induced by the quotient map from G to G/C is totally disconnected
.
The inversion operation on a topological group G is a homeomorphism
from G to itself. Likewise, if a is any element of G, then left or right multiplication by a yields a homeomorphism G → G.
Every topological group can be viewed as a uniform space
in two ways; the left uniformity turns all left multiplications into uniformly continuous maps while the right uniformity turns all right multiplications into uniformly continuous maps. If G is not abelian, then these two need not coincide. The uniform structures allow one to talk about notions such as completeness, uniform continuity and uniform convergence on topological groups.
As a uniform space, every topological group is completely regular. It follows that if a topological group is T0 (Kolmogorov
) then it is already T2 (Hausdorff
), even T3½ (Tychonoff
).
Every subgroup
of a topological group is itself a topological group when given the subspace topology
. If H is a subgroup of G, the set of left or right coset
s G/H is a topological space when given the quotient topology (the finest topology on G/H which makes the natural projection q : G → G/H continuous). One can show that the quotient map q : G → G/H is always open.
Every open subgroup H is also closed, since the complement of H is the open set given by the union of open sets gH for g in G \ H.
If H is a normal subgroup
of G, then the factor group, G/H becomes a topological group when given the quotient topology. However, if H is not closed
in the topology of G, then G/H will not be T0 even if G is. It is therefore natural to restrict oneself to the category of T0 topological groups, and restrict the definition of normal to normal and closed.
The isomorphism theorem
s known from ordinary group theory are not always true in the topological setting. This is because a bijective homomorphism need not be an isomorphism of topological groups. The theorems are valid if one places certain restrictions on the maps involved. For example, the first isomorphism theorem states that if f : G → H is a homomorphism then G/ker(f) is isomorphic to im(f) if and only if the map f is open onto its image.
If H is a subgroup of G then the closure
of H is also a subgroup. Likewise, if H is a normal subgroup, the closure of H is normal.
A topological group G is Hausdorff if and only if the trivial one-element subgroup is closed in G. If G is not Hausdorff then one can obtain a Hausdorff group by passing to the quotient space G/K where K is the closure of the identity. This is equivalent to taking the Kolmogorov quotient of G.
The fundamental group
of a topological group is always abelian
. This is a special case of the fact that the fundamental group of an H-space is abelian, since topological groups are H-space
s.
are the locally compact group
s, because they admit a natural notion of measure
and integral
, given by the Haar measure
. The theory of group representation
s is almost identical for finite groups and for compact topological groups. In general, σ-compact Baire
topological groups are locally compact.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a topological group is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G together with a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a topological structure. Thus, one may perform algebraic operations, because of the group structure, and one may talk about continuous functions, because of the topology.
Topological groups, along with continuous group actions, are used to study continuous symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, which have many applications, for example in physics.
Formal definition
A topological group G is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
such that the group operations of product:
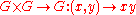
and taking inverses:
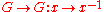
are continuous functions. Here, G × G is viewed as a topological space by using the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
.
Although we do not do so here, many authors require that the topology on G be Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. The reasons, and some equivalent conditions, are discussed below. In the end, this is not a serious restriction—any topological group can be made Hausdorff in a canonical fashion.
In the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, topological groups can be defined concisely as group object
Group object
In category theory, a branch of mathematics, group objects are certain generalizations of groups which are built on more complicated structures than sets...
s in the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, in the same way that ordinary groups are group objects in the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
.
Homomorphisms
A homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
between two topological groups G and H is just a continuous group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
G
 H. An isomorphism
H. An isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of topological groups is a group isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
which is also a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
of the underlying topological spaces. This is stronger than simply requiring a continuous group isomorphism—the inverse must also be continuous. There are examples of topological groups which are isomorphic as ordinary groups but not as topological groups. Indeed, any nondiscrete topological group is also a topological group when considered with the discrete topology. The underlying groups
are the same, but as topological groups there is not an isomorphism.
Topological groups, together with their homomorphisms, form a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Examples
Every group can be trivially made into a topological group by considering it with the discrete topology; such groups are called discrete groupDiscrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
s. In this sense, the theory of topological groups subsumes that of ordinary groups.
The real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R, together with addition as operation and its usual topology, form a topological group. More generally, Euclidean n-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn with addition and standard topology is a topological group. More generally yet, the additive groups of all topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, such as Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s or Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, are topological groups.
The above examples are all abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. Examples of non-abelian topological groups are given by the classical group
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s. For instance, the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n,R) of all invertible n-by-n matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with real entries can be viewed as a topological group with the topology defined by viewing GL(n,R) as a subset of Euclidean space Rn×n.
An example of a topological group which is not a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
is given by the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q with the topology inherited from R. This is a countable space and it does not have the discrete topology. For a nonabelian example, consider the subgroup of rotations of R3 generated by two rotations by irrational multiples of 2π about different axes.
In every Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
with multiplicative identity, the set of invertible elements forms a topological group under multiplication.
Properties
The algebraic and topological structures of a topological group interact in non-trivial ways. For example, in any topological group the identity componentIdentity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
(i.e. the connected component
Locally connected space
In topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
containing the identity element) is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
. This is because if C is the identity component, a*C is the component of G (the group) containing a. In fact, the collection of all left cosets (or right cosets) of C in G is equal to the collection of all components of G. Therefore, the quotient topology induced by the quotient map from G to G/C is totally disconnected
Totally disconnected group
In mathematics, a totally disconnected group is a topological group that is totally disconnected. Such topological groups are necessarily Hausdorff....
.
The inversion operation on a topological group G is a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
from G to itself. Likewise, if a is any element of G, then left or right multiplication by a yields a homeomorphism G → G.
Every topological group can be viewed as a uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
in two ways; the left uniformity turns all left multiplications into uniformly continuous maps while the right uniformity turns all right multiplications into uniformly continuous maps. If G is not abelian, then these two need not coincide. The uniform structures allow one to talk about notions such as completeness, uniform continuity and uniform convergence on topological groups.
As a uniform space, every topological group is completely regular. It follows that if a topological group is T0 (Kolmogorov
Kolmogorov space
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
) then it is already T2 (Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
), even T3½ (Tychonoff
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
).
Every subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of a topological group is itself a topological group when given the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
. If H is a subgroup of G, the set of left or right coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s G/H is a topological space when given the quotient topology (the finest topology on G/H which makes the natural projection q : G → G/H continuous). One can show that the quotient map q : G → G/H is always open.
Every open subgroup H is also closed, since the complement of H is the open set given by the union of open sets gH for g in G \ H.
If H is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G, then the factor group, G/H becomes a topological group when given the quotient topology. However, if H is not closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
in the topology of G, then G/H will not be T0 even if G is. It is therefore natural to restrict oneself to the category of T0 topological groups, and restrict the definition of normal to normal and closed.
The isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
s known from ordinary group theory are not always true in the topological setting. This is because a bijective homomorphism need not be an isomorphism of topological groups. The theorems are valid if one places certain restrictions on the maps involved. For example, the first isomorphism theorem states that if f : G → H is a homomorphism then G/ker(f) is isomorphic to im(f) if and only if the map f is open onto its image.
If H is a subgroup of G then the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of H is also a subgroup. Likewise, if H is a normal subgroup, the closure of H is normal.
A topological group G is Hausdorff if and only if the trivial one-element subgroup is closed in G. If G is not Hausdorff then one can obtain a Hausdorff group by passing to the quotient space G/K where K is the closure of the identity. This is equivalent to taking the Kolmogorov quotient of G.
The fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a topological group is always abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. This is a special case of the fact that the fundamental group of an H-space is abelian, since topological groups are H-space
H-space
In mathematics, an H-space is a topological space X together with a continuous map μ : X × X → X with an identity element e so that μ = μ = x for all x in X...
s.
Relationship to other areas of mathematics
Of particular importance in harmonic analysisHarmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
are the locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s, because they admit a natural notion of measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
and integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, given by the Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
. The theory of group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s is almost identical for finite groups and for compact topological groups. In general, σ-compact Baire
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
topological groups are locally compact.
Generalizations
Various generalizations of topological groups can be obtained by weakening the continuity conditions:- A semitopological group is a group G with a topology such that for each c in G the two functions G → G defined by
 and
and  are continuous.
are continuous. - A quasitopological group is a semitopological group in which the function mapping elements to their inverses is also continuous.
- A paratopological groupParatopological groupIn mathematics, a paratopological group is a topological semigroup that is algebraically a group. In other words, it is a group G with a topology such that the group's product operation is a continuous function from G × G to G...
is a group with a topology such that the group operation is continuous.

