
Modular representation theory
Encyclopedia
Modular representation theory is a branch of mathematics
, and that part of representation theory
that studies linear representations of finite group
G over a field
K of positive characteristic
. As well as having applications to group theory, modular representations arise
naturally in other branches of mathematics, such as algebraic geometry
, coding theory
, combinatorics
and number theory
.
Within finite group theory
, character-theoretic results proved
by Richard Brauer
using modular representation theory played
an important role in early progress towards the
classification of finite simple groups
, especially for simple groups whose characterization was not amenable to purely group-theoretic methods because their Sylow 2 subgroups were too small in an appropriate sense. Also, a general result on embedding of elements of order 2 in finite groups called the Z* theorem, proved by George Glauberman
using the theory developed by Brauer, was particularly useful in the classification program.
If the characteristic of K does not divide the order of G, then modular representations are completely reducible, as with ordinary
(characteristic 0) representations, by virtue of Maschke's theorem
. The proof of Maschke's theorem relies on being able to divide by the group order, which is not meaningful when the order of G is divisible by the characteristic of K. In that case, representations need not be
completely reducible, unlike the ordinary (and the coprime characteristic) case. Much of the discussion below implicitly assumes
that the field K is sufficiently large (for example, K algebraically closed suffices), otherwise some statements need refinement.
of some finite groups.
The systematic study of modular representations, when the characteristic divides the order of the group, was started by and continued by him for the next few decades.
of two elements over F2 is equivalent to the problem of finding matrices whose square is the identity matrix. Over every field of characteristic other than 2, there is always a basis such that the matrix can be written as a diagonal matrix with only 1 or −1 occurring on the diagonal, such as
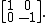
Over F2, there are many other possible matrices, such as

Over an algebraically closed field of positive characteristic,
the representation theory of a finite cyclic group is fully explained
by the theory of the Jordan normal form
. Non-diagonal Jordan
forms occur when the characteristic divides the order of the group.
K[G] (which is the K-vector space
with K-basis consisting of the elements of G, endowed with
algebra multiplication by extending the multiplication
of G by linearity) is an Artinian ring
.
When the order of G is divisible by the characteristic of K, the group algebra is not semisimple
, hence has non-zero Jacobson radical
. In that case, there are finite-dimensional modules for the group algebra that are not projective module
s. By contrast, in the characteristic 0 case every irreducible representation is a direct summand of the regular representation
, hence is projective.
from about 1940 onwards to study in greater depth the relationships between the
characteristic p representation theory, ordinary character theory and structure of G, especially as the latter relates to the embedding of, and relationships between, its p-subgroups. Such results can be applied in group theory
to problems not directly phrased in terms of representations.
Brauer introduced the notion now known as the Brauer character. When K is algebraically closed of positive characteristic p, there is a bijection between roots of unity in K and complex roots of unity of order prime to p. Once a choice of such a bijection is fixed, the Brauer character of a representation assigns to each group element of order coprime to p the sum of complex roots of unity corresponding to the eigenvalues (including multiplicities) of that element in the given representation.
The Brauer character of a representation determines its composition
factors but not, in general, its equivalence type. The irreducible
Brauer characters are those afforded by the simple modules.
These are integral ( though not necessarily non-negative) combinations
of the restrictions to elements of order coprime to p of the ordinary irreducible
characters. Conversely, the restriction to the elements of order prime to p of
each ordinary irreducible character is uniquely expressible as a non-negative
integer combination of irreducible Brauer characters.
group algebra
of the group G over a complete discrete
valuation ring R with residue field K of positive
characteristic p and field of fractions F of characteristic
0. The structure of R[G] is closely related both to
the structure of the group algebra K[G] and to the structure of the semisimple group algebra F[G], and there is much interplay
between the module theory of the three algebras.
Each R[G]-module naturally gives rise to an F[G]-module,
and, by a process often known informally as reduction (mod p),
to a K[G]-module. On the other hand, since R is a
principal ideal domain
, each finite-dimensional F[G]-module
arises by extension of scalars from an R[G]-module. In general,
however, not all K[G]-modules arise as reductions (mod p) of
R[G]-modules. Those that do are liftable.
es of G. In the modular case, the number l(G) of simple modules is equal to the number of conjugacy classes whose elements have order coprime to the relevant prime p, the so-called p-regular classes.
when the characteristic divides the group order, the group algebra may be decomposed as the direct sum of a maximal collection of two-sided ideals known as blocks (when the field K has characteristic 0, or characteristic coprime to the group order, there is also such a decomposition of the group algebra K[G] as a sum of blocks (one for each isomorphism type of simple module), but the situation is relatively transparent (at least when K is sufficiently large): each block is a full matrix algebra over K, the endomorphism ring of the vector space underlying the associated simple module).
To obtain the blocks, the identity element of the group G is decomposed as a sum of primitive idempotents
in Z(R[G]), the center of the group algebra over the maximal order R of F. The block corresponding to the primitive idempotent
e is the two-sided ideal e R[G]. For each indecomposable R[G]-module, there only one such primitive idempotent that does not annihilate it, and the module is said to belong to (or to be in) the corresponding block (in which case, all its composition factors also belong to that block). In particular, each simple module belongs to a unique block. Each ordinary irreducible character may also be assigned to a unique block according to its decomposition as a sum of irreducible Brauer characters. The block containing the trivial module is known as the principal block.
For the group algebra of a finite group, the (isomorphism types of) projective indecomposable modules are in a one-to-one correspondence with the (isomorphism types of) simple modules: the socle
of each projective indecomposable is simple (and isomorphic to the top), and this affords the bijection, as non-isomorphic projective indecomposables have
non-isomorphic socles. The multiplicity of a projective indecomposable module as a summand of the group algebra (viewed as the regular module) is the dimension of its socle (for large enough fields of characteristic zero, this recovers the fact that each simple module occurs with multiplicity equal to its dimension as a direct summand of the regular module).
Each projective indecomposable module (and hence each projective module) in positive characteristic p may be lifted to a module in characteristic 0. Using the ring R as above, with residue field K, the identity element of G may be decomposed as a sum of mutually orthogonal primitive idempotents ( not necessarily
central) of K[G]. Each projective indecomposable K[G]-module is isomorphic to e.K[G] for a primitive idempotent e that occurs in this decomposition. The idempotent e lifts to a primitive idempotent, say E, of R[G], and the left module E.R[G] has reduction (mod p) isomorphic to e.K[G].
second Brauer character is that of the socle of a non-isomorphic projective indecomposable, and 1
if the second Brauer character is that of its own socle. The multiplicity of an ordinary irreducible
character in the character of the lift of a projective indecomposable is equal to the number
of occurrences of the Brauer character of the socle of the projective indecomposable when the restriction of the ordinary character to p-regular elements is expressed as a sum of irreducible Brauer characters.
of the projective indecomposable modules may be calculated as follows:
Given the ordinary irreducible and irreducible Brauer characters of a particular finite group, the irreducible ordinary characters may be decomposed as non-negative integer combinations of the irreducible Brauer characters. The integers involved can be placed in a matrix, with the ordinary irreducible characters assigned rows and the irreducible Brauer characters assigned columns. This is referred to as the decomposition matrix, and is frequently labelled D. It is customary to place the trivial ordinary and Brauer characters in the first row and column respectively. The product of the transpose of D with D itself
results in the Cartan matrix
, usually denoted C; this is a symmetric matrix such that the entries in its j-th row are the multiplicities of the respective simple modules as composition
factors of the j-th projective indecomposable module. The Cartan
matrix is non-singular; in fact, its determinant is a power of the
characteristic of K.
Since a projective indecomposable module in a given block has
all its composition factors in that same block, each block has
its own Cartan matrix.
D of G for which there is a Brauer correspondent
of B for the
subgroup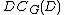 .
.
The defect group of a block is unique up to conjugacy and has a strong influence on the structure of the block. For example, if the defect group is trivial, then the block contains just one simple module, just one ordinary character, the ordinary and Brauer irreducible characters agree on elements of order prime to the relevant characteristic p, and the simple module is projective. At the other extreme, when K has characteristic p, the Sylow p-subgroup of the finite group G is a defect group for the principal block of K[G].
The order of the defect group of a block has many arithmetical characterizations related to representation theory. It is the largest invariant factor of the Cartan matrix of the block, and occurs with
multiplicity one. Also, the power of p dividing the index of the defect group of a block is the greatest common divisor
of the powers of p dividing the dimensions of the simple modules in that block, and this coincides with the greatest common divisor of the powers of p dividing the degrees of the ordinary irreducible characters in that block.
Other relationships between the defect group of a block and character theory include Brauer's result that if no conjugate of the p-part of a group element g is in the defect group of a given block, then each irreducible character in that block vanishes at g. This is a one of many consequences of Brauer's second main theorem.
The defect group of a block also has several characterizations in the more module-theoretic approach to block theory, building on the work of J. A. Green, which associates a p-subgroup
known as the vertex to an indecomposable module, defined in terms of relative projectivity of the module. For example, the vertex of each indecomposable module in a block is contained (up to conjugacy)
in the defect group of the block, and no proper subgroup of the defect group has that property.
Brauer's first main theorem states that the number of blocks of a finite group that have a given p-subgroup as defect group is the same as the corresponding number for the normalizer in the group of that p-subgroup.
The easiest block structure to analyse with non-trivial defect group is when the latter is cyclic. Then there are only finitely many isomorphism types of indecomposable modules in the block, and the structure of the block is by now well understood, by virtue of work of Brauer, E.C. Dade, J.A.Green and J.G.Thompson, among others. In all other cases, there are infinitely many isomorphism types of indecomposable modules in the block.
Blocks whose defect groups are not cyclic can be divided into two types: tame and wild. The tame blocks (which only occur for the prime 2) have as a defect group a dihedral group
, semidihedral group or (generalized) quaternion group
, and their structure has been broadly determined in a series of papers by Karin Erdmann
. The indecomposable modules in wild blocks are extremely difficult to classify, even in principle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and that part of representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
that studies linear representations of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
G over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K of positive characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
. As well as having applications to group theory, modular representations arise
naturally in other branches of mathematics, such as algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
Within finite group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, character-theoretic results proved
by Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
using modular representation theory played
an important role in early progress towards the
classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, especially for simple groups whose characterization was not amenable to purely group-theoretic methods because their Sylow 2 subgroups were too small in an appropriate sense. Also, a general result on embedding of elements of order 2 in finite groups called the Z* theorem, proved by George Glauberman
George Glauberman
George Glauberman is a mathematician at the University of Chicago who works on finite simple groups. He proved the ZJ theorem and the Z* theorem....
using the theory developed by Brauer, was particularly useful in the classification program.
If the characteristic of K does not divide the order of G, then modular representations are completely reducible, as with ordinary
(characteristic 0) representations, by virtue of Maschke's theorem
Maschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
. The proof of Maschke's theorem relies on being able to divide by the group order, which is not meaningful when the order of G is divisible by the characteristic of K. In that case, representations need not be
completely reducible, unlike the ordinary (and the coprime characteristic) case. Much of the discussion below implicitly assumes
that the field K is sufficiently large (for example, K algebraically closed suffices), otherwise some statements need refinement.
History
The earliest work on representation theory over finite fields is by who showed that when p does not divide the order of the group then the representation theory is similar to that in characteristic 0. He also investigated modular invariantsModular invariant of a group
In mathematics, a modular invariant of a group is an invariant of a finite group acting on a vector space of positive characteristic...
of some finite groups.
The systematic study of modular representations, when the characteristic divides the order of the group, was started by and continued by him for the next few decades.
Example
Finding a representation of the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of two elements over F2 is equivalent to the problem of finding matrices whose square is the identity matrix. Over every field of characteristic other than 2, there is always a basis such that the matrix can be written as a diagonal matrix with only 1 or −1 occurring on the diagonal, such as
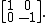
Over F2, there are many other possible matrices, such as

Over an algebraically closed field of positive characteristic,
the representation theory of a finite cyclic group is fully explained
by the theory of the Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
. Non-diagonal Jordan
forms occur when the characteristic divides the order of the group.
Ring theory interpretation
Given a field K and a finite group G, the group algebraGroup algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
K[G] (which is the K-vector space
with K-basis consisting of the elements of G, endowed with
algebra multiplication by extending the multiplication
of G by linearity) is an Artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
.
When the order of G is divisible by the characteristic of K, the group algebra is not semisimple
Semisimple algebraic group
In mathematics, especially in the areas of abstract algebra and algebraic geometry studying linear algebraic groups, a semisimple algebraic group is a type of matrix group which behaves much like a semisimple Lie algebra or semisimple ring.- Definition :...
, hence has non-zero Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
. In that case, there are finite-dimensional modules for the group algebra that are not projective module
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
s. By contrast, in the characteristic 0 case every irreducible representation is a direct summand of the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
, hence is projective.
Brauer characters
Modular representation theory was developed by Richard BrauerRichard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
from about 1940 onwards to study in greater depth the relationships between the
characteristic p representation theory, ordinary character theory and structure of G, especially as the latter relates to the embedding of, and relationships between, its p-subgroups. Such results can be applied in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
to problems not directly phrased in terms of representations.
Brauer introduced the notion now known as the Brauer character. When K is algebraically closed of positive characteristic p, there is a bijection between roots of unity in K and complex roots of unity of order prime to p. Once a choice of such a bijection is fixed, the Brauer character of a representation assigns to each group element of order coprime to p the sum of complex roots of unity corresponding to the eigenvalues (including multiplicities) of that element in the given representation.
The Brauer character of a representation determines its composition
factors but not, in general, its equivalence type. The irreducible
Brauer characters are those afforded by the simple modules.
These are integral ( though not necessarily non-negative) combinations
of the restrictions to elements of order coprime to p of the ordinary irreducible
characters. Conversely, the restriction to the elements of order prime to p of
each ordinary irreducible character is uniquely expressible as a non-negative
integer combination of irreducible Brauer characters.
Reduction (mod p)
In the theory initially developed by Brauer, the link between ordinary representation theory and modular representation theory is best exemplified by considering thegroup algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
of the group G over a complete discrete
valuation ring R with residue field K of positive
characteristic p and field of fractions F of characteristic
0. The structure of R[G] is closely related both to
the structure of the group algebra K[G] and to the structure of the semisimple group algebra F[G], and there is much interplay
between the module theory of the three algebras.
Each R[G]-module naturally gives rise to an F[G]-module,
and, by a process often known informally as reduction (mod p),
to a K[G]-module. On the other hand, since R is a
principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
, each finite-dimensional F[G]-module
arises by extension of scalars from an R[G]-module. In general,
however, not all K[G]-modules arise as reductions (mod p) of
R[G]-modules. Those that do are liftable.
Number of simple modules
In ordinary representation theory, the number of simple modules k(G) is equal to the number of conjugacy classConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es of G. In the modular case, the number l(G) of simple modules is equal to the number of conjugacy classes whose elements have order coprime to the relevant prime p, the so-called p-regular classes.
Blocks and the structure of the group algebra
In modular representation theory, while Maschke's theorem does not holdwhen the characteristic divides the group order, the group algebra may be decomposed as the direct sum of a maximal collection of two-sided ideals known as blocks (when the field K has characteristic 0, or characteristic coprime to the group order, there is also such a decomposition of the group algebra K[G] as a sum of blocks (one for each isomorphism type of simple module), but the situation is relatively transparent (at least when K is sufficiently large): each block is a full matrix algebra over K, the endomorphism ring of the vector space underlying the associated simple module).
To obtain the blocks, the identity element of the group G is decomposed as a sum of primitive idempotents
in Z(R[G]), the center of the group algebra over the maximal order R of F. The block corresponding to the primitive idempotent
e is the two-sided ideal e R[G]. For each indecomposable R[G]-module, there only one such primitive idempotent that does not annihilate it, and the module is said to belong to (or to be in) the corresponding block (in which case, all its composition factors also belong to that block). In particular, each simple module belongs to a unique block. Each ordinary irreducible character may also be assigned to a unique block according to its decomposition as a sum of irreducible Brauer characters. The block containing the trivial module is known as the principal block.
Projective modules
In ordinary representation theory, every indecomposable module is irreducible, and so every module is projective. However, the simple modules with characteristic dividing the group order are rarely projective. Indeed, if a simple module is projective, then it is the only simple module in its block, which is then isomorphic to the endomorphism algebra of the underlying vector space, a full matrix algebra. In that case, the block is said to have 'defect 0'. Generally, the structure of projective modules is difficult to determine.For the group algebra of a finite group, the (isomorphism types of) projective indecomposable modules are in a one-to-one correspondence with the (isomorphism types of) simple modules: the socle
Socle (mathematics)
-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
of each projective indecomposable is simple (and isomorphic to the top), and this affords the bijection, as non-isomorphic projective indecomposables have
non-isomorphic socles. The multiplicity of a projective indecomposable module as a summand of the group algebra (viewed as the regular module) is the dimension of its socle (for large enough fields of characteristic zero, this recovers the fact that each simple module occurs with multiplicity equal to its dimension as a direct summand of the regular module).
Each projective indecomposable module (and hence each projective module) in positive characteristic p may be lifted to a module in characteristic 0. Using the ring R as above, with residue field K, the identity element of G may be decomposed as a sum of mutually orthogonal primitive idempotents ( not necessarily
central) of K[G]. Each projective indecomposable K[G]-module is isomorphic to e.K[G] for a primitive idempotent e that occurs in this decomposition. The idempotent e lifts to a primitive idempotent, say E, of R[G], and the left module E.R[G] has reduction (mod p) isomorphic to e.K[G].
Some orthogonality relations for Brauer characters
When a projective module is lifted, the associated character vanishes on all elements of order divisible by p, and (with consistent choice of roots of unity), agrees with the Brauer character of the original characteristic p module on p-regular elements. The (usual character-ring) inner product of the Brauer character of a projective indecomposable with any other Brauer character can thus be defined: this is 0 if thesecond Brauer character is that of the socle of a non-isomorphic projective indecomposable, and 1
if the second Brauer character is that of its own socle. The multiplicity of an ordinary irreducible
character in the character of the lift of a projective indecomposable is equal to the number
of occurrences of the Brauer character of the socle of the projective indecomposable when the restriction of the ordinary character to p-regular elements is expressed as a sum of irreducible Brauer characters.
Decomposition matrix and Cartan matrix
The composition factorsComposition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
of the projective indecomposable modules may be calculated as follows:
Given the ordinary irreducible and irreducible Brauer characters of a particular finite group, the irreducible ordinary characters may be decomposed as non-negative integer combinations of the irreducible Brauer characters. The integers involved can be placed in a matrix, with the ordinary irreducible characters assigned rows and the irreducible Brauer characters assigned columns. This is referred to as the decomposition matrix, and is frequently labelled D. It is customary to place the trivial ordinary and Brauer characters in the first row and column respectively. The product of the transpose of D with D itself
results in the Cartan matrix
Cartan matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...
, usually denoted C; this is a symmetric matrix such that the entries in its j-th row are the multiplicities of the respective simple modules as composition
factors of the j-th projective indecomposable module. The Cartan
matrix is non-singular; in fact, its determinant is a power of the
characteristic of K.
Since a projective indecomposable module in a given block has
all its composition factors in that same block, each block has
its own Cartan matrix.
Defect groups
To each block B of the group algebra K[G], Brauer associated a certain p-subgroup, known as its defect group (where p is the characteristic of K). Formally, it is the largest p-subgroupD of G for which there is a Brauer correspondent
Brauer's three main theorems
Brauer's main theorems are three theorems in representation theory of finite groups linking the blocks of a finite group with those of its p-local subgroups, that is to say, the normalizers of its non-trivial p-subgroups....
of B for the
subgroup
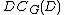 .
.The defect group of a block is unique up to conjugacy and has a strong influence on the structure of the block. For example, if the defect group is trivial, then the block contains just one simple module, just one ordinary character, the ordinary and Brauer irreducible characters agree on elements of order prime to the relevant characteristic p, and the simple module is projective. At the other extreme, when K has characteristic p, the Sylow p-subgroup of the finite group G is a defect group for the principal block of K[G].
The order of the defect group of a block has many arithmetical characterizations related to representation theory. It is the largest invariant factor of the Cartan matrix of the block, and occurs with
multiplicity one. Also, the power of p dividing the index of the defect group of a block is the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of the powers of p dividing the dimensions of the simple modules in that block, and this coincides with the greatest common divisor of the powers of p dividing the degrees of the ordinary irreducible characters in that block.
Other relationships between the defect group of a block and character theory include Brauer's result that if no conjugate of the p-part of a group element g is in the defect group of a given block, then each irreducible character in that block vanishes at g. This is a one of many consequences of Brauer's second main theorem.
The defect group of a block also has several characterizations in the more module-theoretic approach to block theory, building on the work of J. A. Green, which associates a p-subgroup
known as the vertex to an indecomposable module, defined in terms of relative projectivity of the module. For example, the vertex of each indecomposable module in a block is contained (up to conjugacy)
in the defect group of the block, and no proper subgroup of the defect group has that property.
Brauer's first main theorem states that the number of blocks of a finite group that have a given p-subgroup as defect group is the same as the corresponding number for the normalizer in the group of that p-subgroup.
The easiest block structure to analyse with non-trivial defect group is when the latter is cyclic. Then there are only finitely many isomorphism types of indecomposable modules in the block, and the structure of the block is by now well understood, by virtue of work of Brauer, E.C. Dade, J.A.Green and J.G.Thompson, among others. In all other cases, there are infinitely many isomorphism types of indecomposable modules in the block.
Blocks whose defect groups are not cyclic can be divided into two types: tame and wild. The tame blocks (which only occur for the prime 2) have as a defect group a dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
, semidihedral group or (generalized) quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
, and their structure has been broadly determined in a series of papers by Karin Erdmann
Karin Erdmann
Karin Erdmann is a German mathematician specializing in the areas of algebra known as representation theory and homological algebra...
. The indecomposable modules in wild blocks are extremely difficult to classify, even in principle.

