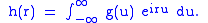Selberg trace formula
Encyclopedia
In mathematics
, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation
of G on the space L2(G/Γ) of square-integrable function
s, where G is a Lie group
and Γ a cofinite discrete group
. The character is given by the trace of certain functions on G.
The simplest case is when Γ is cocompact, when the representation breaks up into discrete summands. Here the trace formula is an extension of the Frobenius formula for the character of an induced representation
of finite groups. When Γ is the cocompact subgroup Z of the real numbers G=R, the Selberg trace formula is essentially the Poisson summation formula
.
The case when G/Γ is not compact is harder, because there is a continuous spectrum
, described using Eisenstein series
. Selberg worked out the non-compact case when G is the group SL2(R); the extension to higher rank groups is the Arthur-Selberg trace formula.
When Γ is the fundamental group of a Riemann surface
, the Selberg trace formula describes the spectrum of differential operators such as the Laplacian in terms of geometric data involving the lengths of geodesics on the Riemann surface. In this case the Selberg trace formula is formally similar to the explicit formulas relating the zeros of the Riemann zeta function to prime numbers, with the zeta zeros corresponding to eigenvalues of the Laplacian, and the primes corresponding to geodesics. Motivated by the analogy, Selberg introduced the Selberg zeta function of a Riemann surface, whose analytic properties are encoded by the Selberg trace formula.
S. The initial publication in 1956 of Atle Selberg
dealt with this case, its Laplacian differential operator and its powers. The traces of powers of a Laplacian can be used to define the Selberg zeta function. The interest of this case was the analogy between the formula obtained, and the explicit formulae of prime number
theory. Here the closed geodesic
s on S play the role of prime numbers.
At the same time, interest in the traces of Hecke operator
s was linked to the Eichler-Selberg trace formula, of Selberg and Martin Eichler
, for a Hecke operator acting on a vector space of cusp form
s of a given weight, for a given congruence subgroup
of the modular group
. Here the trace of the identity operator is the dimension of the vector space, i.e. the dimension of the space of modular forms of a given type: a quantity traditionally calculated by means of the Riemann-Roch theorem.
. For instance, using the trace theorem Eichler and Shimura calculated the Hasse-Weil L-functions associated to modular curve
s; Goro Shimura
's methods by-passed the analysis involved in the trace formula. The development of parabolic cohomology (from Eichler cohomology) provided a purely algebraic setting based on group cohomology
, taking account of the cusps
characteristic of non-compact Riemann surfaces and modular curves.
The trace formula also has purely differential-geometric applications. For instance, by a result of Buser, the length spectrum of a Riemann surface
is an isospectral invariant, essentially by the trace formula.
was largely motivated by the requirement to separate out the continuous spectrum
, which is characteristic of the non-compact case.
The trace formula is often given for algebraic groups over the adeles rather than for Lie groups, because this makes the corresponding discrete subgroup Γ into an algebraic group over a field which is technically easier to work with.
Contemporary successors of the theory are the Arthur-Selberg trace formula applying to the case of general semisimple G, and the many studies of the trace formula in the Langlands philosophy (dealing with technical issues such as endoscopy).
can be written as
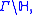
where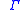
is a subgroup of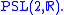 
The Selberg trace formula for this case is easier than the general case because the surface is compact so there is no continuous spectrum, and the group Γ has no parabolic or elliptic elements (other than the identity).
Then the spectrum for the Laplace-Beltrami operator
on
is discrete and real, since the Laplace operator is self adjoint with compact resolvent
; that is
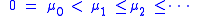
where the eigenvalues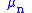
correspond to Γ-invariant eigenfunctions 
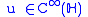of the Laplacian; in other words
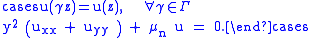
Using the variable substitution
the eigenvalues are labeled
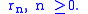
Then the Selberg trace formula is given by
The right hand side is a sum over conjugacy classes of the group Γ, with the first term corresponding to the identity element and the remaining terms forming a sum over the other conjugacy classes
(which are all hyperbolic in this case).
The function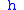
has to be an analytic function on 
, satisfy
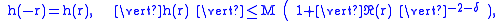
where the numbers
and 
are positive constants. The function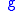 
is the Fourier transform of 
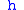, that is,
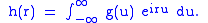
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Selberg trace formula, introduced by , is an expression for the character of the unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of G on the space L2(G/Γ) of square-integrable function
Square-integrable function
In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...
s, where G is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
and Γ a cofinite discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
. The character is given by the trace of certain functions on G.
The simplest case is when Γ is cocompact, when the representation breaks up into discrete summands. Here the trace formula is an extension of the Frobenius formula for the character of an induced representation
Induced representation
In mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
of finite groups. When Γ is the cocompact subgroup Z of the real numbers G=R, the Selberg trace formula is essentially the Poisson summation formula
Poisson summation formula
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...
.
The case when G/Γ is not compact is harder, because there is a continuous spectrum
Continuous spectrum
The spectrum of a linear operator is commonly divided into three parts: point spectrum, continuous spectrum, and residual spectrum.If H is a topological vector space and A:H \to H is a linear map, the spectrum of A is the set of complex numbers \lambda such that A - \lambda I : H \to H is not...
, described using Eisenstein series
Eisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
. Selberg worked out the non-compact case when G is the group SL2(R); the extension to higher rank groups is the Arthur-Selberg trace formula.
When Γ is the fundamental group of a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, the Selberg trace formula describes the spectrum of differential operators such as the Laplacian in terms of geometric data involving the lengths of geodesics on the Riemann surface. In this case the Selberg trace formula is formally similar to the explicit formulas relating the zeros of the Riemann zeta function to prime numbers, with the zeta zeros corresponding to eigenvalues of the Laplacian, and the primes corresponding to geodesics. Motivated by the analogy, Selberg introduced the Selberg zeta function of a Riemann surface, whose analytic properties are encoded by the Selberg trace formula.
Early history
Cases of particular interest include those for which the space is a compact Riemann surfaceCompact Riemann surface
In mathematics, a compact Riemann surface is a complex manifold of dimension one that is a compact space. Riemann surfaces are generally classified first into the compact and the open .A compact Riemann surface C that is a...
S. The initial publication in 1956 of Atle Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
dealt with this case, its Laplacian differential operator and its powers. The traces of powers of a Laplacian can be used to define the Selberg zeta function. The interest of this case was the analogy between the formula obtained, and the explicit formulae of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
theory. Here the closed geodesic
Closed geodesic
In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold M is the projection of a closed orbit of the geodesic flow on M.-Examples:On the unit sphere, every great circle is an example of a closed geodesic...
s on S play the role of prime numbers.
At the same time, interest in the traces of Hecke operator
Hecke operator
In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by , is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations....
s was linked to the Eichler-Selberg trace formula, of Selberg and Martin Eichler
Martin Eichler
Martin Eichler was a German number theorist.Eichler received his Ph.D. from the Martin Luther University of Halle-Wittenberg in 1936....
, for a Hecke operator acting on a vector space of cusp form
Cusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
s of a given weight, for a given congruence subgroup
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
. Here the trace of the identity operator is the dimension of the vector space, i.e. the dimension of the space of modular forms of a given type: a quantity traditionally calculated by means of the Riemann-Roch theorem.
Applications
The trace formula has applications to arithmetic geometry and number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. For instance, using the trace theorem Eichler and Shimura calculated the Hasse-Weil L-functions associated to modular curve
Modular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
s; Goro Shimura
Goro Shimura
is a Japanese mathematician, and currently a professor emeritus of mathematics at Princeton University.Shimura was a colleague and a friend of Yutaka Taniyama...
's methods by-passed the analysis involved in the trace formula. The development of parabolic cohomology (from Eichler cohomology) provided a purely algebraic setting based on group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
, taking account of the cusps
Cusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
characteristic of non-compact Riemann surfaces and modular curves.
The trace formula also has purely differential-geometric applications. For instance, by a result of Buser, the length spectrum of a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
is an isospectral invariant, essentially by the trace formula.
Later work
The general theory of Eisenstein seriesEisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
was largely motivated by the requirement to separate out the continuous spectrum
Continuous spectrum
The spectrum of a linear operator is commonly divided into three parts: point spectrum, continuous spectrum, and residual spectrum.If H is a topological vector space and A:H \to H is a linear map, the spectrum of A is the set of complex numbers \lambda such that A - \lambda I : H \to H is not...
, which is characteristic of the non-compact case.
The trace formula is often given for algebraic groups over the adeles rather than for Lie groups, because this makes the corresponding discrete subgroup Γ into an algebraic group over a field which is technically easier to work with.
Contemporary successors of the theory are the Arthur-Selberg trace formula applying to the case of general semisimple G, and the many studies of the trace formula in the Langlands philosophy (dealing with technical issues such as endoscopy).
Selberg trace formula for compact hyperbolic surfaces
A compact hyperbolic surface can be written aswhere
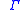is a subgroup of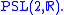 The Selberg trace formula for this case is easier than the general case because the surface is compact so there is no continuous spectrum, and the group Γ has no parabolic or elliptic elements (other than the identity).
Then the spectrum for the Laplace-Beltrami operator
Laplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
on
is discrete and real, since the Laplace operator is self adjoint with compact resolventResolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
; that is
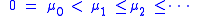
where the eigenvalues
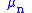correspond to Γ-invariant eigenfunctions 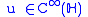of the Laplacian; in other words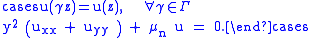Using the variable substitution
the eigenvalues are labeled
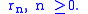
Then the Selberg trace formula is given by
The right hand side is a sum over conjugacy classes of the group Γ, with the first term corresponding to the identity element and the remaining terms forming a sum over the other conjugacy classes
(which are all hyperbolic in this case).The function
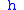has to be an analytic function on , satisfy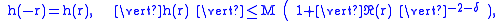where the numbers
and are positive constants. The function 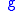is the Fourier transform of 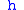, that is,